Lo studio delle catene di tolleranze raccoglie e sintetizza molte informazioni di prodotto e di processo: la geometria delle parti, le tolleranze dei singoli componenti, i metodi di assemblaggio, le tolleranze delle attrezzature di produzione, le quote funzionali e di controllo della produzione consentendo di evidenziare fin dalle prime fasi di progettazione le possibili anomalie geometriche e di porvi tempestivamente rimedio.
L’insieme delle quote tollerate consecutive di elementi dei pezzi assemblati in un gruppo o complessivo, costituisce una catena (in inglese stack, pila), che ha un notevole impatto su funzionalità e costo di produzione. Attraverso di essa si vede come i singoli errori sui componenti di un dispositivo possano combinarsi e propagarsi fino ad influenzare una dimensione funzionale dell’assemblato. La valutazione della catena di tolleranze è quindi fondamentale per le analisi di montaggio e la determinazione di giochi ed interferenze risultanti. Lo studio delle catene di quote permette inoltre di prescrivere le tolleranze più ampie compatibili con la funzione richiesta, e comprendere le dimensioni critiche degli elementi assemblati, stabilendo le corrette relazioni tra dimensioni, tolleranze e funzione del prodotto. Inoltre, lo studio delle catene raccoglie e sintetizza molte informazioni di prodotto e di processo: la geometria delle parti, le tolleranze dei singoli componenti, i metodi di assemblaggio, le tolleranze delle attrezzature di produzione, le quote funzionali e di controllo della produzione consentendo di evidenziare fin dalle prime fasi di progettazione le possibili anomalie geometriche e di porvi tempestivamente rimedio
Due approcci di base
Esistono due approcci di base per ottenere questo risultato: il primo metodo, conosciuto come analisi delle tolleranze, calcola la tolleranza risultante nel complessivo partendo dalle tolleranze note dei singoli componenti (fig. 1). Il secondo, noto come sintesi o allocazione delle tolleranze, stabilisce a priori la tolleranza del complessivo e attribuisce le tolleranze ai singoli componenti. La metodologia del calcolo della catena delle tolleranze può essere applicata su assiemi per verificare se tutti i componenti si montano in ogni condizione di tolleranza o se i giochi previsti tra diversi componenti abbiano una variabilità compatibile con il funzionamento; su pezzi singoli può essere impiegata per calcolare la variabilità di caratteristiche geometriche in seguito alle lavorazioni tecnologiche che le realizzano, ad esempio l’interasse tra fori.
Di solito un valore di tolleranza ridotto in un assemblato assicura funzionalità e prestazioni corrette, ma implica costi di produzione elevati, mentre nell’assegnazione delle tolleranze si dovrebbero sempre bilanciare prestazioni, funzionalità e costi. Nella risoluzione della catena si può applicare il cosiddetto metodo delle condizioni limite (Worst case, “caso peggiore”, cioè) oppure il metodo statistico. Nel primo caso, più conservativo, si assume che le dimensioni dei componenti siano situate agli estremi del campo di tolleranza prefissato e che queste si combinano tra di loro influendo nel modo più negativo possibile sul risultato finale. Nella realtà è però difficile che si presentino contemporaneamente diverse misure esattamente al limite del campo di tolleranza, per cui si pone rimedio adottando il calcolo statistico in cui si assegna una distribuzione di probabilità ad ogni misura compresa nel campo di tolleranza specificato e come risultato si caratterizza la distribuzione di probabilità della misura risultante.
Le tecniche di calcolo

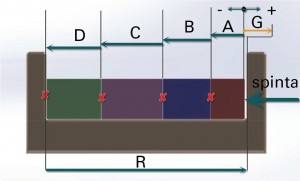
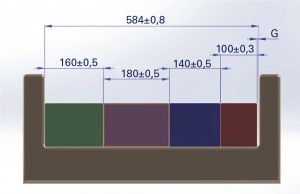
Le tecniche di calcolo verranno descritte, in modo esemplificativo, al complessivo di figura 2, in cui sono visibili una serie di blocchi prismatici all’interno di una struttura. I singoli blocchi vengono montati in serie nella scanalatura del pezzo base in modo da lasciare uno spazio nominale di 4 mm. Si supponga in un primo tempo di conoscere le singole tolleranze dei componenti e quindi si applichi la tecnica di analisi delle tolleranze.
G=R-(A+B+C+D)=584-(160+180+140+100)= 4 mm
Gmax=Rmax-(A+B+C+D)min=584,4-(159,7+179,6+139,8+99,8)=5,5 mm
Gmin=Rmin-(A+B+C+D)max=583,6-(160,3+180.4+140,2+100,2)=2,5 mm
G= 4 ± 1,5 mm
Viene così dimostrato che in una catena di tolleranze, la somma di tutte le tolleranze della catena deve eguagliare la tolleranza sul gioco:
tG = ∑ti = tR + tA + tB + tC + tD= 0,8+ 0,6 + 0,8 + 0,4 + 0,4 = 3 mm
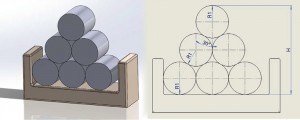
La stessa tecnica può essere usata per calcolare l’altezza di una serie di rulli impilati come in figura 3.
H = R1 + R1cos(30°) + 2R1cos(30°) + R1cos(30°) + R1 = R1[1+cos(30°) + 2cos(30°) + cos(30°) + 1]
H = R1[2 + 4cos(30°)]=5,464 R1
Se R1 = 90 mm, allora H= 491,76 mm
La tolleranza sull’altezza sarà uguale a:
tH = 5,464 tR1
se tR1 = 0,2 mm allora tH ≈ 1 mm
Si applichi adesso la procedura di allocazione delle tolleranze, supponendo che il progettista abbia stabilito a priori una tolleranza sul gioco e si valutino le tolleranze dei singoli componenti, che assicurano tale tolleranza complessiva. Il progettista per poter effettuare un calcolo di catena tolleranze accurato deve poter reperire o definire le seguenti informazioni:
- geometria delle parti (modelli 3D, disegni, dimensioni nominali)
- sequenza di assemblaggio (ordine di montaggio delle parti)
- riferimenti di montaggio delle parti (quali sono i dispositivi che orientano, posizionano e bloccano un pezzo su di un altro, possono anche esserci attrezzi esterni)
- quote funzionali da analizzare (ad esempio il gioco assiale tra una parte rotante ed una fissa)
- obiettivi di tolleranza da raggiungere sulle quote funzionali
- tolleranze da assegnare ai singoli componenti per l’impostazione iniziale del calcolo (norme ISO, standard aziendali …)
- Per la risoluzione della catena può essere proposto un metodo non solo semplice, ma che consente anche di ottimizzare i risultati in funzione degli obiettivi di progetto, attraverso l’utilizzo di un modulo o di un foglio Excel che permette il calcolo del gioco organizzando le quote in modo completo e sistematico.
Gli step da seguire sono i seguenti:
- Identificare le quote dei componenti che hanno influenza sulla funzione obiettivo e quindi sul gioco finale.
2. Si immagini di spingere i componenti in una direzione determinata, in modo da visualizzare la zona del gap risultante.
3. La catena di quote viene contrassegnata da un origine ed un orientamento (positivo ad esempio nel verso di percorrenza destro); in questo modo tutte le quote percorse verso sinistra vanno sottratte nella catena, mentre quelle percorse verso destra vanno sommate.
4. Ogni quota viene indicata con un vettore.
Come primo tentativo, si possono impostare le tolleranze generali ISO 2768-m
In pratica, ciascuna quota è descritta mediante un vettore orientato, definito con il punto di applicazione, ovvero la linea di riferimento da cui parte la quota, la direzione della quota stessa ed il verso di percorrenza identificato con la freccia all’altra estremità del vettore. Il modulo del vettore è pari alla lunghezza descritta dalla quota. Le varie dimensioni identificate nella catena permettono di raggiungere l’altra linea di riferimento della misura, seguendo un percorso chiuso in cui tutti i vettori si susseguono ordinatamente. Il vettore somma di tutte le quote identificate è la quota funzionale di interesse ed il suo verso risulta opposto all’ultima dimensione in catena (o alla prima). Nella figura 4, il punto di partenza di una dimensione è identificato con un cerchietto pieno e l’altra estremità è rappresentata con la freccia del vettore che indica anche la direzione.
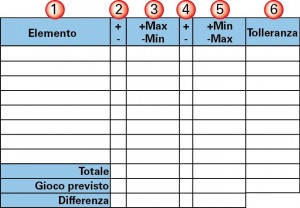
Per facilitare i calcoli e organizzare le quote in forma completa e sistematica, è utile far riferimento al modulo illustrato in figura 6, in cui le colonne hanno i seguenti significati: 1: colonna dove viene descritto o codificato l’elemento in catena; 2, 3, 4 e 5: in queste quattro colonne viene immesso il massimo e minimo valore per ciascuna dimensione in catena. Se il verso di percorrenza è negativo, viene indicato un segno – nelle colonne 2 e 4, il valore minimo della dimensione dell’elemento nella colonna 3 e il valore massimo nella colonna 5. Se invece il verso è positivo, viene indicato un segno + nelle colonne 2 e 4, il valore massimo della dimensione dell’elemento nella colonna 3 e il valore minimo nella colonna 5. 6 : differenza tra la colonna 3 e 5, che costituisce la tolleranza, quindi sempre positiva. Nella tabella viene indicato il totale, cioè il gioco ottenuto sommando le colonne 3 ed 5, e la tolleranza del gioco con la somma dei valori della colonna 6; poiché la somma di tutte le tolleranze della catena deve uguagliare la tolleranza del gioco.
Con riferimento alla figura 4, partendo dall’origine prefissata, si percorra la catena di quote assumendo inizialmente un verso di percorrenza verso sinistra, per poi chiudere la catena col vettore gioco G. Il vettore “gioco” ha sempre verso opposto al primo o al penultimo, e poiché è diretto verso destra, il gioco è positivo. È possibile inserire le quote con le rispettive tolleranze, assegnando come primo tentativo le tolleranze secondo ISO 2768-m, come in figura 5.
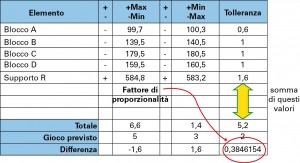
Il risultato finale è visibile in figura 7: rispetto al gioco previsto di 4±1, bisogna recuperare -1.6 sulla colonna 3 e +1.6 sulla colonna 5. Le strategie di ottimizzazione del gioco consentono di allocare le tolleranze rispettando i vincoli dei costi di produzione, tenendo conto anche delle quote più critiche ai fini funzionali. Il modo più semplice per allocare le tolleranze è quello di applicare un fattore di proporzionalità P, in modo da riportare le tolleranze ai valori di progetto:
tG = ∑ti = tR + tA + tB + tC + tD= 2 mm
2 = P(tR + tA + tB + tC + tD) = P (1,6+0,6+1+1+1) = 5,2P
P = 2/5,2 = 0,384
Moltiplicando le tolleranze dei componenti in catena per il fattore P, si otterranno I valori di figura 8 che verranno opportunamente arrotondati.
Un metodo più versatile per l’assegnazione di tolleranze è l’utilizzo dei fattori peso. Utilizzando questo algoritmo, il progettista assegna un peso a ciascun tolleranza della catena e il sistema distribuisce una frazione di tolleranza corrispondente per ciascun componente. Un fattore di peso più grande per un dato componente significa che sarà assegnato ad esso una frazione più grande della tolleranza disponibile. In questo modo, delle tolleranza più ampie possono essere applicate a quelle quote che sono più costose o difficili da tenere, migliorando così la producibilità del progetto.
La formula da usare in questo caso è:
tG = ∑PWiti
Si può provare ad assegnare dei fattori peso a ognuno dei componenti, immaginando che siano di materiale diverso e tenendo presente la difficoltà della lavorazione; ad esempio ai blocchi A, B, C, D si può assegnare rispettivamente un fattore peso di 20, 10, 10, 20 e un fattore peso 20 anche al supporto R.
tG = 2 = P[(20/80)tR + (20/80)tA + (10/80)tB + (10/80)tC + (20/80)tD ]
tG = 2 = P[(20/80)1,6 + (20/80)0,6 + (10/80) + (10/80) + (20/80)] = P(0,4+0,15+0,125+0,125+0,25)
P = 2/1,05 = 1,9
tR = 1,9(20/80)1,6 = 0,76 mm
tA = 1,9(20/80)0,6 = 0,285 mm
tB = 1,9(10/80) = 0,2375 mm
tC = 1,9(10/80) = 0,2375 mm
tD = 1,9(20/80) = 0,475 mm

Il risultato finale riportato in figura 9; anche in questo caso conviene effettuare gli opportuni arrotondamenti.
Lo svantaggio nell’applicazione del metodo del “caso peggiore” si riscontra nelle tolleranze allocate sui vari componenti, che risultano spesso molto strette e i corrispondenti costi di produzione, elevati. Come soluzione si può pensare di utilizzare un’impostazione probabilistica, a cui si assegna a ogni tolleranza in catena una distribuzione di proprietà. Uno dei metodi più usati è il modello statistico RSS (Root Sum of Squares), che presuppone che i processi con cui sono prodotti i singoli componenti sono in controllo statistico e seguono una distribuzione normale; inoltre, la capability dei processi con cui sono prodotti i componenti viene considerata essere pari a +/-3 sigma e la media dei processi è centrata sulla valore medio della tolleranza. In questo caso però ci dobbiamo aspettare una difettosità dell’assieme tipica di un processo 3 sigma centrato (99.73% assemblability). In questo modo nell’impostare il calcolo catena tolleranze su base statistica, una volta scelto il valore di capacità di processo si dimostra che:
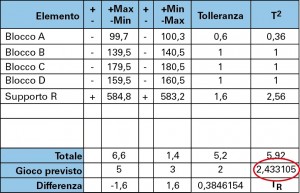
Nella figura 10 è riportata la catena tolleranze della quota funzionale G che verrà ora calcolata con l’impostazione statistica. La tabella di sinistra, modificata rispetto a quella vista per il calcolo algebrico, riporta il risultato del calcolo statistico. I campi di tolleranza sono riportati nella colonna “Tolleranza” e nella colonna T2 si riportano i loro quadrati. Nella riga “Totale” si riporta la sommatoria dei valori nominali delle tolleranze, e dei loro quadrati. Alla fine della colonna dell’ultimo totale si riporta la tolleranza risultante TR calcolato su base statistica. Applichiamo il metodo del fattore di proporzionalità per allocare le tolleranze:
Da cui:
Le tolleranze saranno scalate del fattore calcolato e riportate nella tabella di fig. 11:
tR = 0,822*1,6 = 1,315 mm

tA = 0,822*0,6 = 0,493 mm
tB = 0,822*1 = 0,822 mm
tC = 0,822*1 = 0,822 mm
tD = 0,822*1 = 0,822 mm
Le dimensioni limiti si calcolano sommando e sottraendo al valore nominale della misura la metà del campo di tolleranza calcolato. Nelle ultime due righe si riportano gli obiettivi e la differenza tra di essi e il calcolato.
Naturalmente, anche in questo caso si è proceduto a un arrotondamento dei risultati. Non è più possibile allocare direttamente i residui in quanto la formulazione non è lineare.

Esempio applicativo: dispositivo di trasmissione
Applichiamo la metodologia esposta a un dispositivo di trasmissione, costituito da un basamento (1) a cui si collegano due montanti (2) mediante 4 spine (3) e 4 viti (4). I montanti sono assemblati in modo da utilizzare lo stesso componente. La condizione funzionale è la rotazione del gruppo puleggia-albero con un gioco compreso tra 2,5 e 0,5 mm (fig. 13).
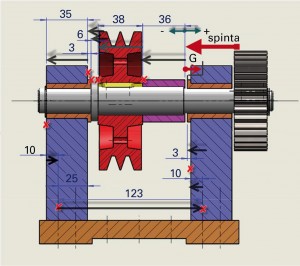
Per applicare in modo corretto la catena vettoriale, si immagini di spingere il distanziale verso sinistra e di assegnare l’origine in corrispondenza del gioco risultante come in figura 14. La catena viene percorsa in senso antiorario, intercettando gli assi dei fori delle spine di riferimento. Il vettore gioco ha verso positivo, essendo diretto verso destra.
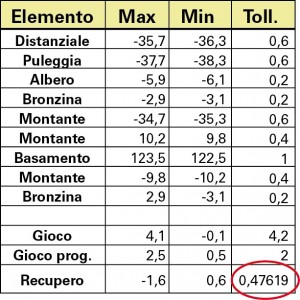
La figura 15 mostra il risultato della catena, dove è evidente un recupero di -1,6 mm sulla colonna Max e di 0,6 mm sulla colonna Min.
Il fattore di proporzionalità si ottiene dalla formula:
tG = P Σ ti
2 = P (0,6+0,6+0,2+0,2+0,6+0,4+1+0,4+0,2) = 4,2P
Da cui deriva P = 0,4762
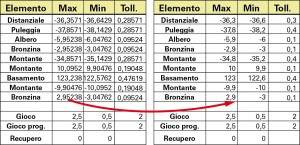
Moltiplicando ciascuna tolleranza per il fattore di ridimensionamento P, si ottengono i valori di figura 16. Si può notare che il risultato della tolleranza del gioco sia sostanzialmente corretto, anche se più grande di 0,5 rispetto ai valori di progetto. Basterà quindi aumentare di 0,5 mm la dimensione del distanziale per ritrovare il gioco nominale compreso tra 2,5 e 0,5 mm. Anche con questo caso converrà arrotondare i valori limiti, in modo da ottenere il risultato di figura 17.
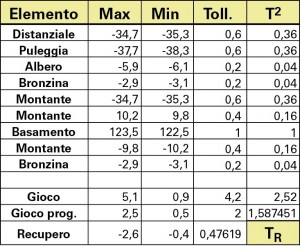
Applichiamo al caso in esame l’analisi statistica RSS, calcolando il fattore di ridimensionamento secondo i valori della tabella di figura 18:
In questo caso le tolleranze dei componenti possono essere addirittura ampliate di un fattore pari a 1.26 con dei costi di fabbricazione ridotti.