Gli elementi 3D finiti solidi

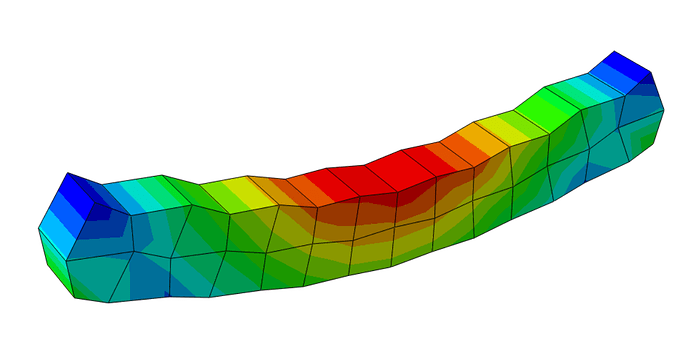
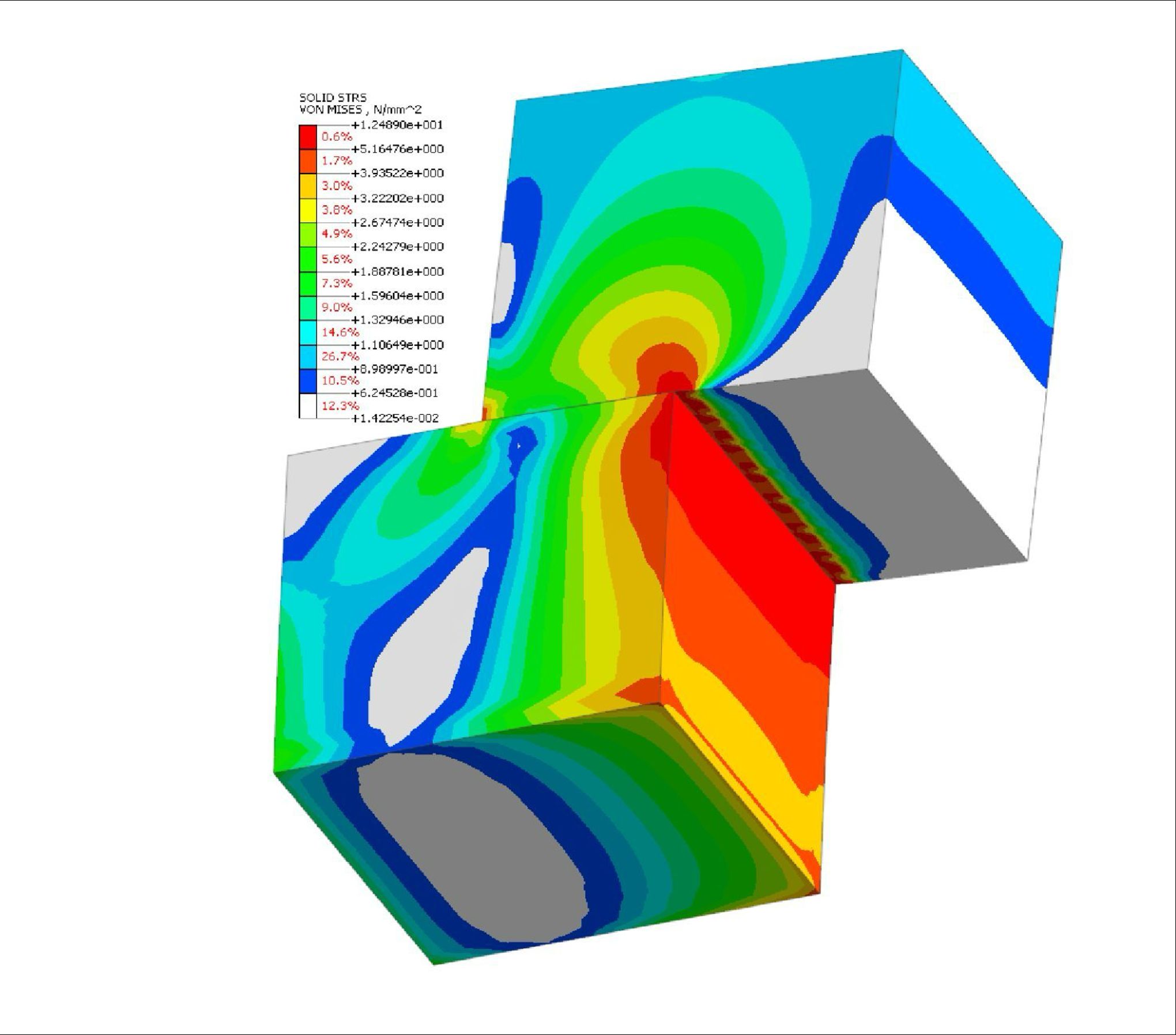
Nei quaderni precedenti dedicati agli elementi finiti sono state introdotte varie tipologie di elementi finiti con particolare attenzione a quelle più semplici come elementi asta, elementi trave ed elementi piani. In questo articolo verranno descritti gli elementi tridimensionali (elementi 3D), ovvero quelli elementi che non portano con sé in modo intrinseco delle semplificazioni come avveniva per gli elementi visti in precedenza.

di Franco Concli

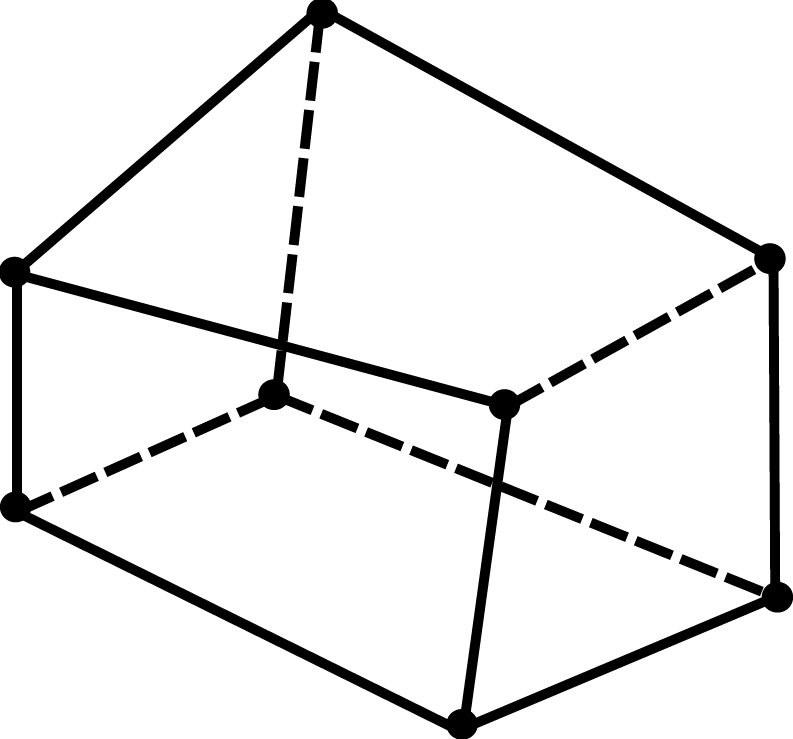
Il termine elemento 3D si riferisce a un corpo solido tridimensionale che non è limitato per quanto riguarda la forma, il carico, le proprietà del materiale e le condizioni al contorno. Il campo di spostamento di questa tipologia di elementi è descritto da tre componenti, u, v, e w. Le forme più comuni per gli elementi finiti solidi (3D) sono i tetraedri e gli esaedri, i cui nodi hanno ognuno 3 gradi di libertà (DOF) traslazionali.

La relazione costitutiva di un materiale linearmente elastico è scritta come:

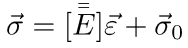
Per un materiale isotropo ciò si traduce in:

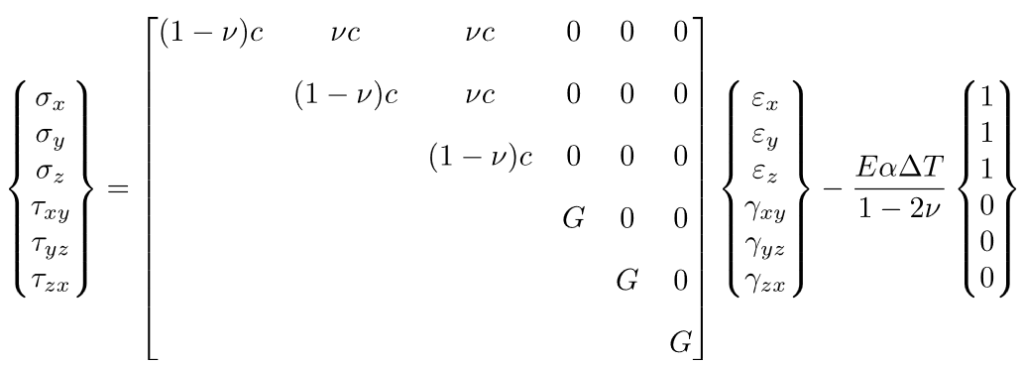
con 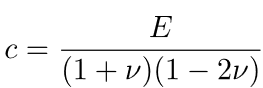 in cui E è il modulo elastico, G è il modulo torsionale e ν il coefficiente di Poisson.

Nel caso di simmetria assiale, tutto ciò può essere semplificato riducendosi a:

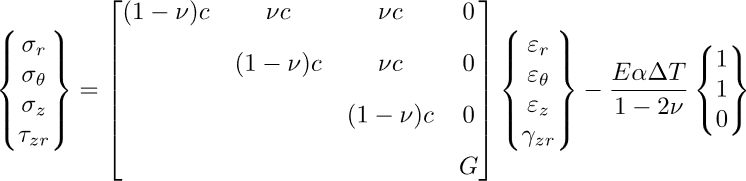
Sotto l’ipotesi di piccoli spostamenti, le componenti di deformazione nelle coordinate possono essere espresse come:

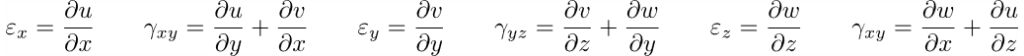
Nel caso di solidi assialsimmetrici conviene invece esprimere tutto in coordinate cilindriche. In queste condizioni, la componente circonferenziale di spostamento v risulta essere zero. La componente radiale u e quella assiale w sono funzioni del raggio (r) e della posizione assiale (z). Le deformazioni di taglio γ_rθ e γ_θz risultano anche nulle. Le uniche componenti diverse da zero sono dunque:

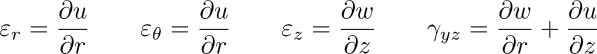
Si noti come uno spostamento circonferenziale nullo non implica una deformazione circonferenziale pari a zero.

Gli spostamenti u all’interno di un elemento sono interpolati a partire dai valori nodali d in

il modo consueto, i.e. , con N matrice della funzione di forma. Per gli elementi 3D questo può essere scritto come:

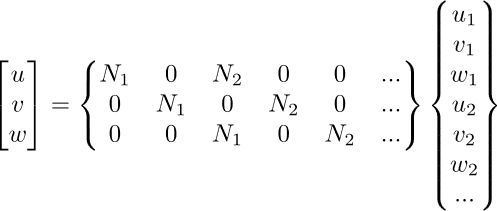
Analogamente, nel caso assialsimmetrico, gli spostamenti risultano:

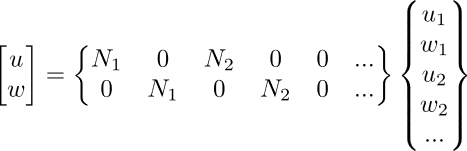
La sostituzione di  nella relazione deformazione-spostamento permette di definire la matrice deformazione-spostamento B, che a sua volta entra nell’integrando della formula per la matrice di rigidezza degli elementi k.

La matrice di rigidezza dell’elemento viene calcolata come:

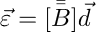
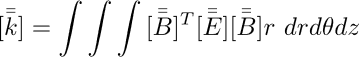
per gli elementi 3D e come:

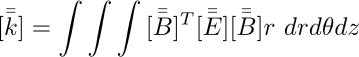
per gli elementi assialsimmetrici. Il passaggio da elementi 2D ad elementi 3D comporta quindi l’aggiunta di un’ulteriore componente. Il comportamento e le limitazioni di specifici elementi 3D sono molto simili a quelli delle loro controparti 2D, con formulazioni analoghe per le relazioni di rigidezza e deformazione-spostamento.

Tipi di elementi 3E

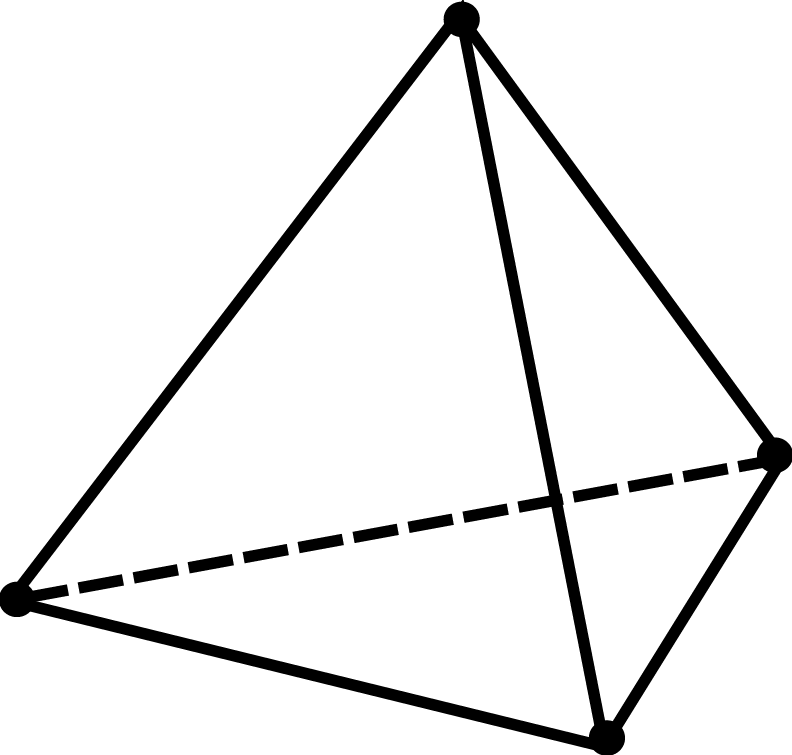
Tetraedro a deformazione costante

Questa tipologia di elemento ha tre DOF traslazionali in ciascuno dei suoi quattro nodi, per un totale di 12 DOF. In termini di coordinate generalizzate beta, il suo campo di spostamento è definito come

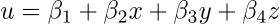
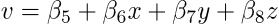
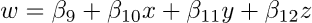
Come l’elemento piano a deformazione costante (T3), il tetraedro di deformazione costante è accurato solo quando le deformazioni risultano essere pressoché costanti all’interno dello spazio modellato con l’elemento. Esso non è quindi in grado di rappresentare correttamente i campi di flessione o torsione se l’asse di flessione o torsione interseca dell’elemento o giace vicino ad esso.

Tetraedro a deformazione lineare

Questo elemento ha dieci nodi, ciascuno con tre DOF traslazionali, per un totale di 30 gradi di libertà. Il suo campo di spostamento, in termini di coordinate generalizzate, può essere ottenuto sommando i sei modi quadratici a ciascuna delle espressioni per u, v, e w. Come il triangolo a sei nodi (T6), il tetraedro a dieci nodi è caratterizzato da un campo lineare di deformazione. Grazie a questa sua caratteristica, esso può rappresentare esattamente campi di pura flessione. A seconda delle coordinate assegnate ai nodi, gli spigoli degli elementi (non deformati) possono essere rettilinei o curvilinei.

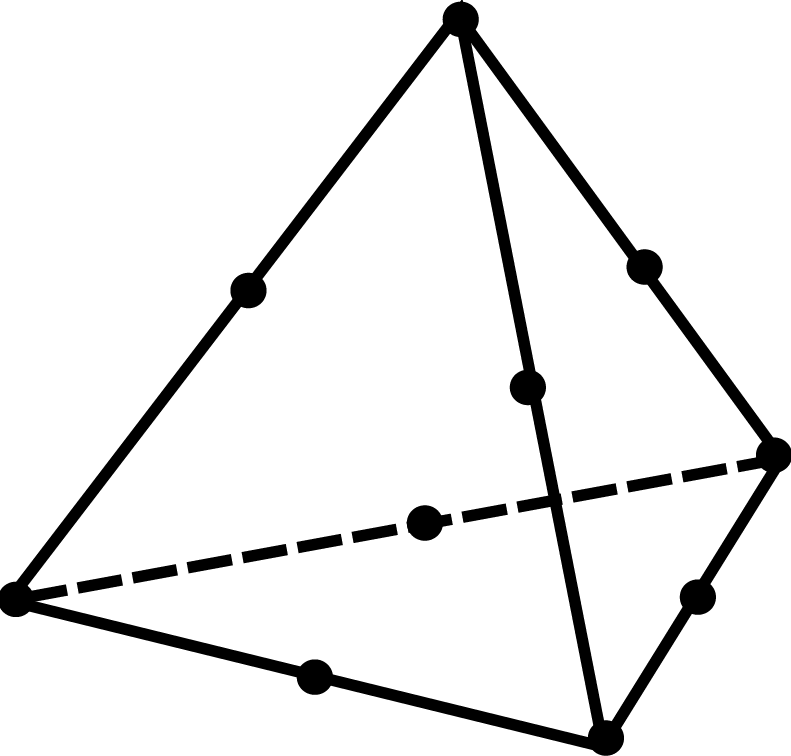
Esaedro trilineare

L’esaedro trilineare, comunemente chiamato elemento brick a otto nodi, è spesso preferito agli elementi tetraedrici per le sue caratteristiche prestazionali superiori. La geometria e gli spostamenti dell’esaedro trilineare sono definiti da otto punti nodali situati nei vertici. Nella formulazione isoparametrica, le coordinate naturali dell’elemento sono definite nell’intervallo -1, +1 lungo ciascun asse, i.e. ξ ± 1, η ± 1 e ζ ± 1. In questo modo, l’elemento esaedrico può essere di forma arbitraria.

Il campo di spostamento all’interno dell’elemento segue un’espansione polinomiale completa del primo ordine:

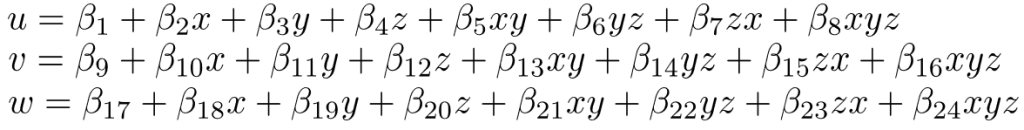
Le espressioni di spostamento possono essere scritte come:

con e .

La matrice di rigidezza dell’elemento in coordinate isoparametriche risulta:

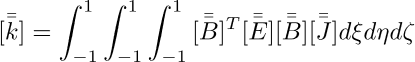
in cui J è la matrice jacobiana che trasforma tra le coordinate cartesiane globali dxdydz in coordinate isoparametriche dξdηdζ. Il suo determinante può essere considerato come il fattore di scala del volume tra i due sistemi di coordinate.

Simile alla sua controparte 2D, il quadrilatero bilineare, l’esaedro trilineare presenta diverse limitazioni. Non è in grado di modellare con precisione la flessione poiché i suoi spigoli rimangono rettilinei anche quando l’elemento si deforma. Se allungato, il quadrilatero lineare soffre del cosiddetto bloccaggio a taglio (shear locking), sviluppando sollecitazioni di taglio fittizie che lo rendono irrealisticamente rigido a flessione.

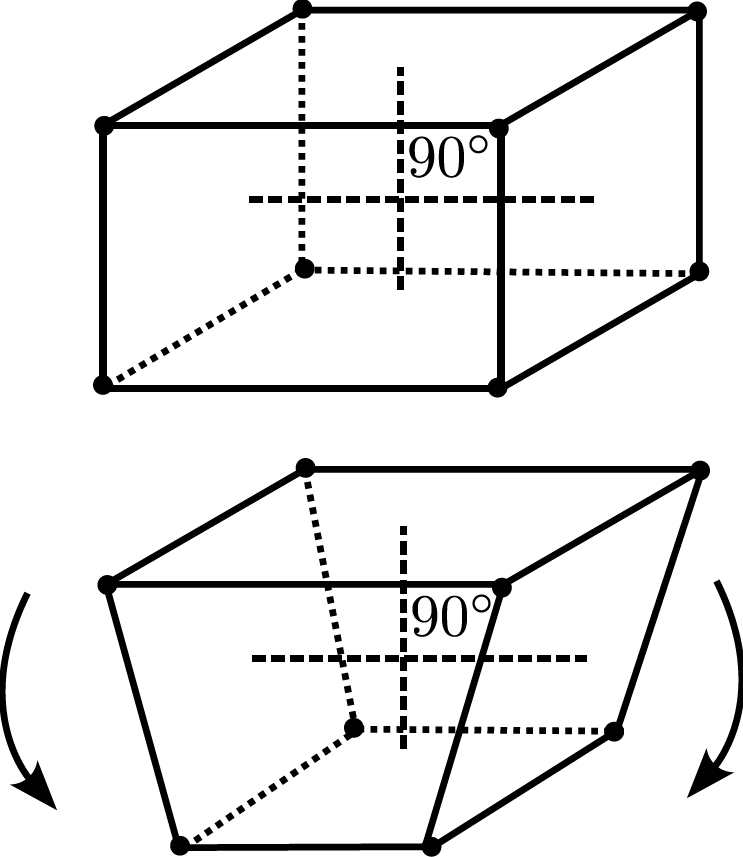
Per questo tipo di elemento vengono utilizzati principalmente due schemi di integrazione. L’integrazione completa che utilizza una quadratura di Gauss 2×2×2 tende ad eliminare gli effetti di bloccaggio a taglio. Lo schema di integrazione ridotto con un singolo punto di integrazione offre un migliore comportamento a flessone, ma introduce notevoli sfide numeriche generando un’instabilità numerica critica, chiamata instabilità a clessidra, dovuta al fatto che alcuni modi di deformazione risultino avere energia di deformazione nulla nei punti di integrazione.

Le linee tratteggiate rimangono orizzontali e verticali formando un angolo di 90◦ anche dopo l’applicazione del carico. Ciò significa che lo sforzo normale e le sollecitazioni di taglio restano nulle nel punto di integrazione e che dunque non si abbia alcuna inerzia di deformazione generata dalla deformazione. Come illustrato nelle Figure 4 e 5, l’elemento può subire una distorsione sostanziale mantenendo angoli di 90° tra le linee di riferimento, con conseguente sollecitazione nulla nel punto di integrazione situato al centro dell’elemento.

La modalità ad energia zero è una risposta non fisica, che può propagare qualora venga utilizzata una griglia di calcolo grossolana, producendo risultati privi di significato.

Esaedro quadratico

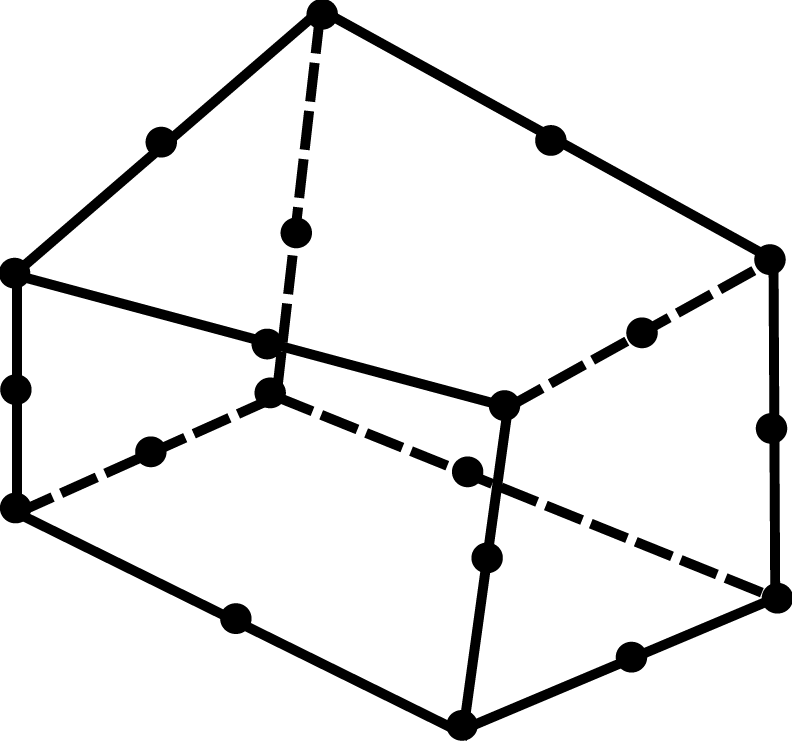
L’esaedro quadratico è un’estensione diretta del quadrilatero quadratico (Q8). Analogamente al tetraedro a deformazione lineare, gli spigoli degli elementi non deformati possono essere rettilinei o curvilinei. Se l’elemento è rettangolare, risulta in grado di modellare esattamente i campi di deformazione lineari.

Se k è integrata con un’integrazione ridotta con una regola di quadratura di Gauss 2x2x2, possono verificarsi sei modi distinti di instabilità a clessidra. I primi tre modi corrispondono a deformazioni a clessidra indipendenti in ciascuna direzione di spostamento u, v, e w. I tre modi aggiuntivi coinvolgono campi di spostamento antisimmetrici in cui le facce opposte dell’elemento si deformano con spostamenti di segno opposto.

Nei problemi piani che utilizzano elementi quadratici, un’instabilità a clessidra non causa problemi significativi. Ma nelle simulazioni 3D, queste instabilità diventano più critiche in quanto gli elementi possono connettersi in sequenza, consentendo alle modalità a clessidra di propagarsi a tutta la mesh.

Per prevenire queste instabilità numeriche mantenendo una ragionevole efficienza computazionale, possono essere impiegati due schemi di integrazione alternativi: il primo approccio utilizza una regola di integrazione specializzata a 14 punti che fornisce un equilibrio tra accuratezza e costo computazionale; un metodo più rigoroso impiega l’integrazione completa con una regola di quadratura di Gauss 3×3×3 (27 punti), che elimina completamente le modalità a clessidra ma con un costo computazionale significativamente più elevato.

Conclusioni

Come si è visto gli elementi finiti solidi sono da un lato più semplici perché non introducono semplificazioni, dall’altro sono molto onerosi da un punto di vista computazionale e portano con se problemi come l’instabilità a clessidra. Nel prossimo numero si mostreranno alcuni esempi applicativi di questa tipologia di elementi.