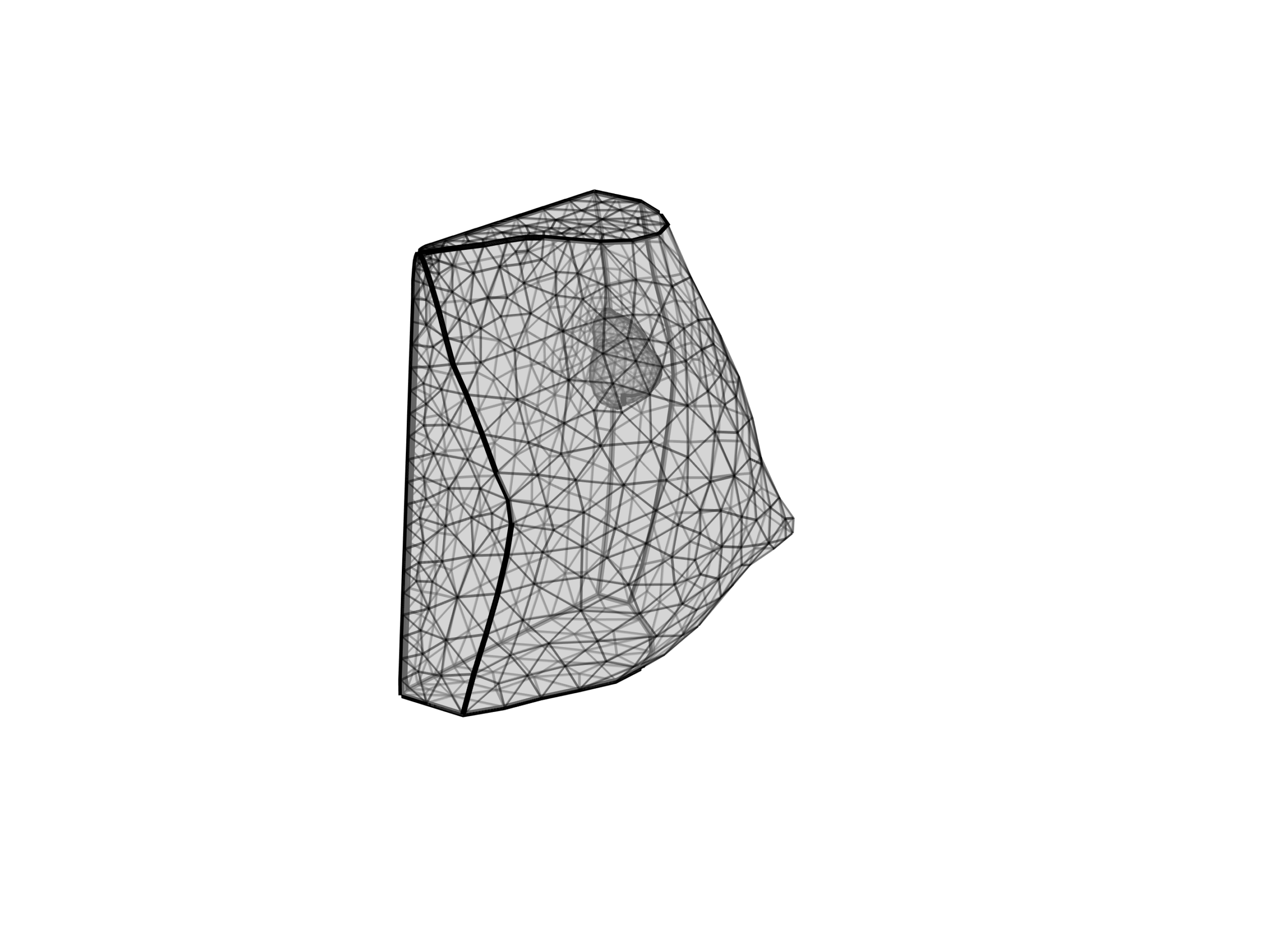
Trucchi per il calcolo di distanze funzionali: una tolleranza di localizzazione controlla lo spostamento consentito di una singolarità geometrica (feature) rispetto ad una posizione teoricamente esatta, definita da un sistema di riferimento (Seconda parte). Se nella prima parte era stata messa in evidenza la difficoltà dei metrologi di verificare le tolleranze geometriche di localizzazione, ora vediamo quali sono i trucchi per il calcolo di distanze funzionali.
Nella prima parte era stata messa in evidenza la difficoltà dei metrologi di verificare le tolleranze geometriche di localizzazione, soprattutto a causa degli effetti di alcuni modificatori, la cui decodifica presuppone una conoscenza approfondita delle normative ISO GPS e ASME.
Si consideri ad esempio il disegno del componente di Figura 1 (in apertura), quotato secondo l’ultima versione dello standard ASME Y14.5 del 2018. In questo caso, la normativa consente l’utilizzo di un controllo generale sul profilo, per cui su tutte le superfici viene applicata una tolleranza sul profilo di 0.4 mm, simmetrica rispetto alla posizione del profilo ideale. Il controllo sul profilo si applica anche alle superfici di riferimento (datum features) A, B e C, per cui non sono state indicate le tolleranze di forma e orientamento, solitamente utilizzate per qualificare i datum. Il pattern dei due fori da 22 mm viene localizzato rispetto al sistema di riferimento (Datum Reference Frame, DRF) A, B e C.
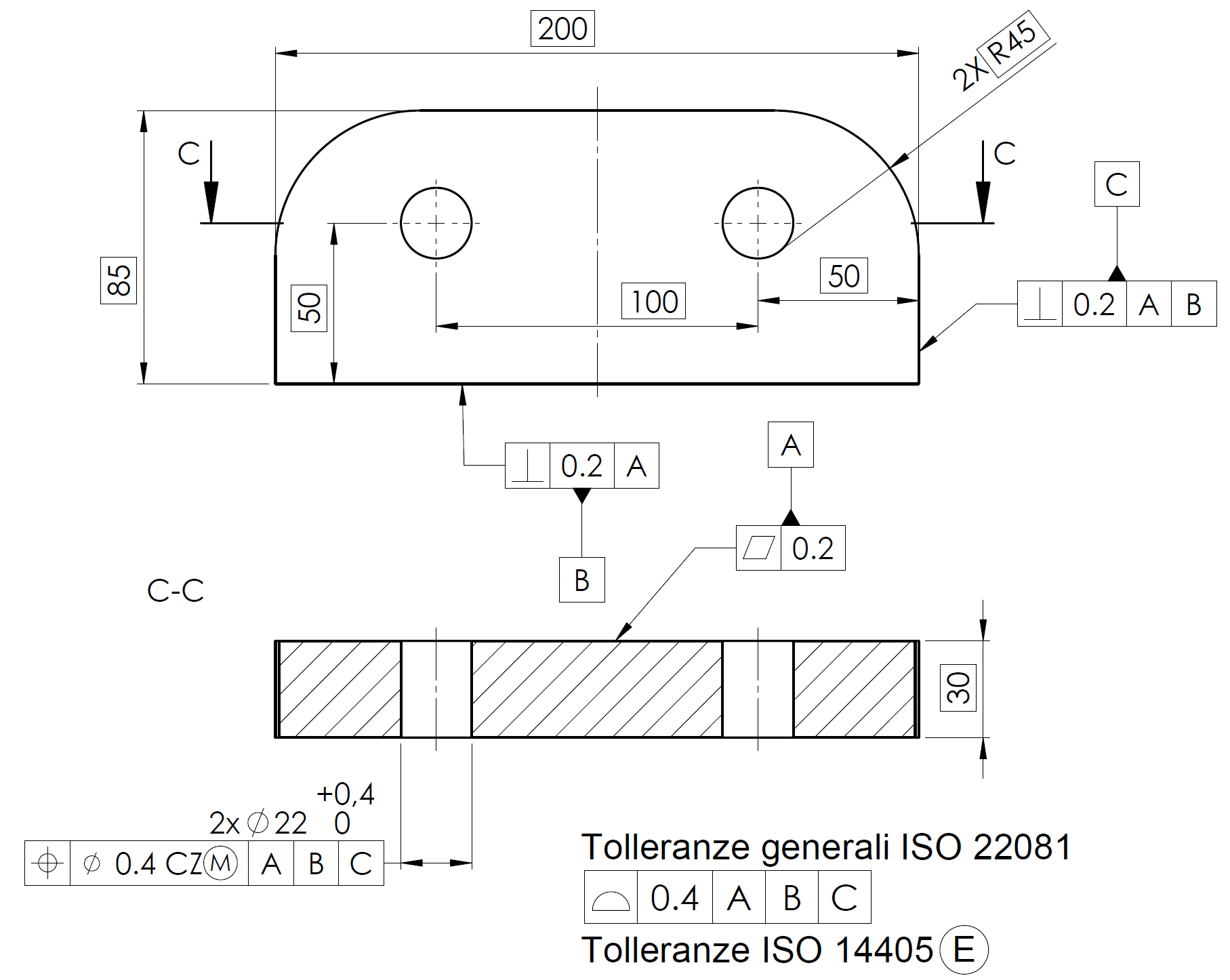
In Figura 2 viene riportato lo stesso disegno realizzato però con lo standard ISO: la tolleranza generale sul profilo viene indicata attraverso il nuovo standard ISO 22081 che sancisce, in modo inequivocabile, che il controllo non debba essere applicato ai datum indicati nel riquadro. Pertanto, risulta necessario qualificare nel disegno gli elementi di riferimento con una tolleranza di planarità sul riferimento primario e di perpendicolarità sul riferimento secondario e terziario (in questo caso si controlla anche la planarità). Da notare anche la presenza del modificatore CZ (Combined Zone) che definisce il pattern dei due fori. A prima vista, le tolleranze sui datum del disegno ISO appaiono dimezzate (0.2 mm) rispetto a quelle del disegno ASME (profilo generale 0.4 mm): come giustificare questa differenza?
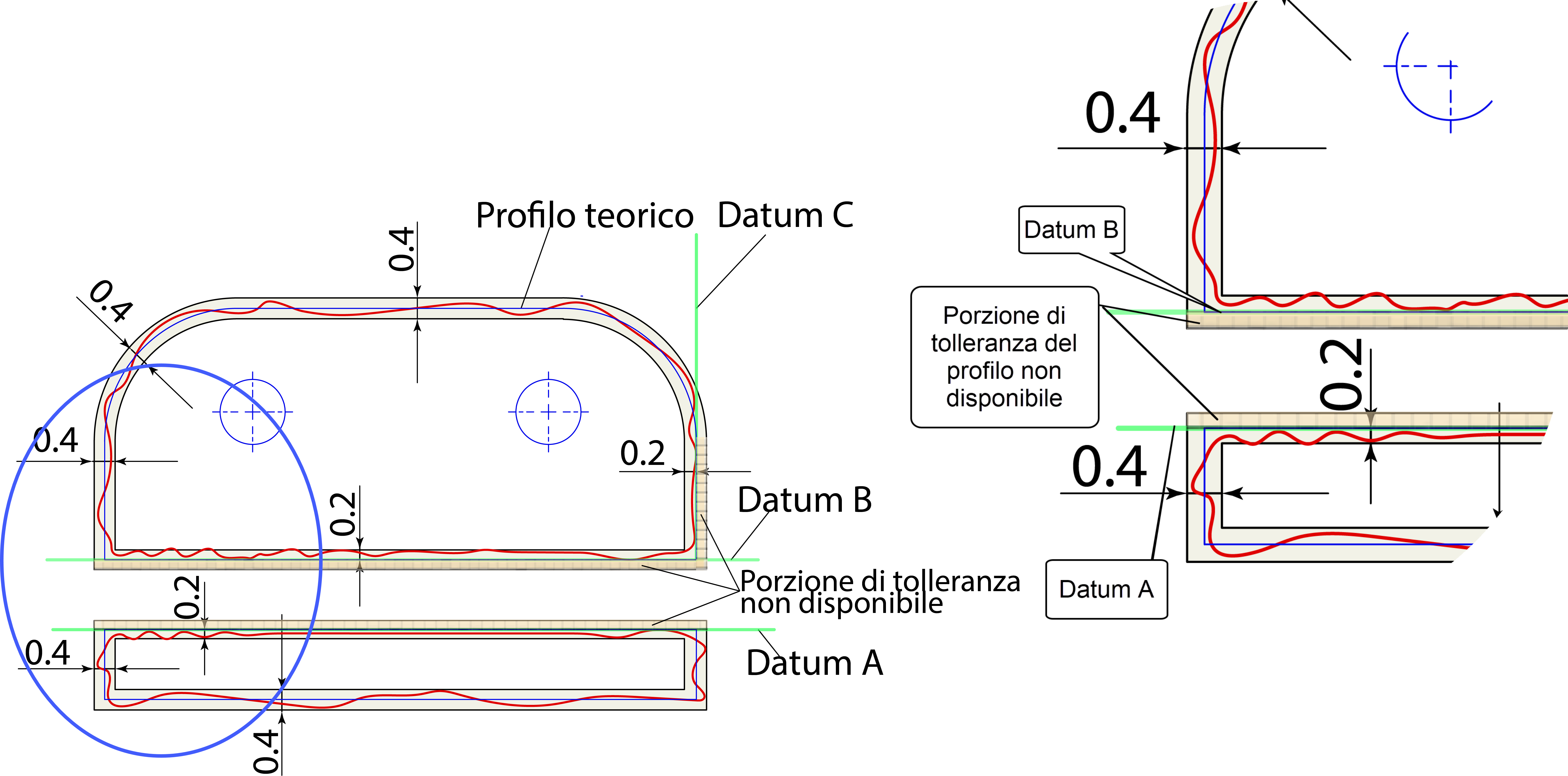
Nella Figura 3 è visibile l’effetto della tolleranza generale del profilo sul componente rappresentato con lo standard ASME nella figura 1. La zona di tolleranza è costituita da due superfici limiti di offset, distanti 0.4 mm e perfettamente simmetriche rispetto al profilo teorico (disegnato con una linea blu). Per poter accettare il componente durante la verifica, il profilo del pezzo reale (rappresentato con una linea rossa) deve stare all’interno di questa fascia. Ma cosa avviene in corrispondenza delle superfici di riferimento? Poiché il datum è per definizione la controparte geometria perfetta del datum feature, in questo caso è costituito da un piano tangente al profilo, avente teoricamente distanza zero dalla geometria ideale. In definiva, come si evidenza nella stessa figura, in corrispondenza dei datum, è disponibile solo metà della tolleranza del profilo (in questo caso 0.2 mm, che è lo stesso valore indicato sui datum del disegno secondo lo standard ISO). La lunghezza nominale del componente è 200 mm, ma a causa della tolleranza generale sul profilo, la lunghezza limite massima è 200,2 mm ( e non 200,4), mentre la lunghezza limite minima tiene conto anche del controllo del profilo sul riferimento C, per cui diventa uguale a 199,6 mm.
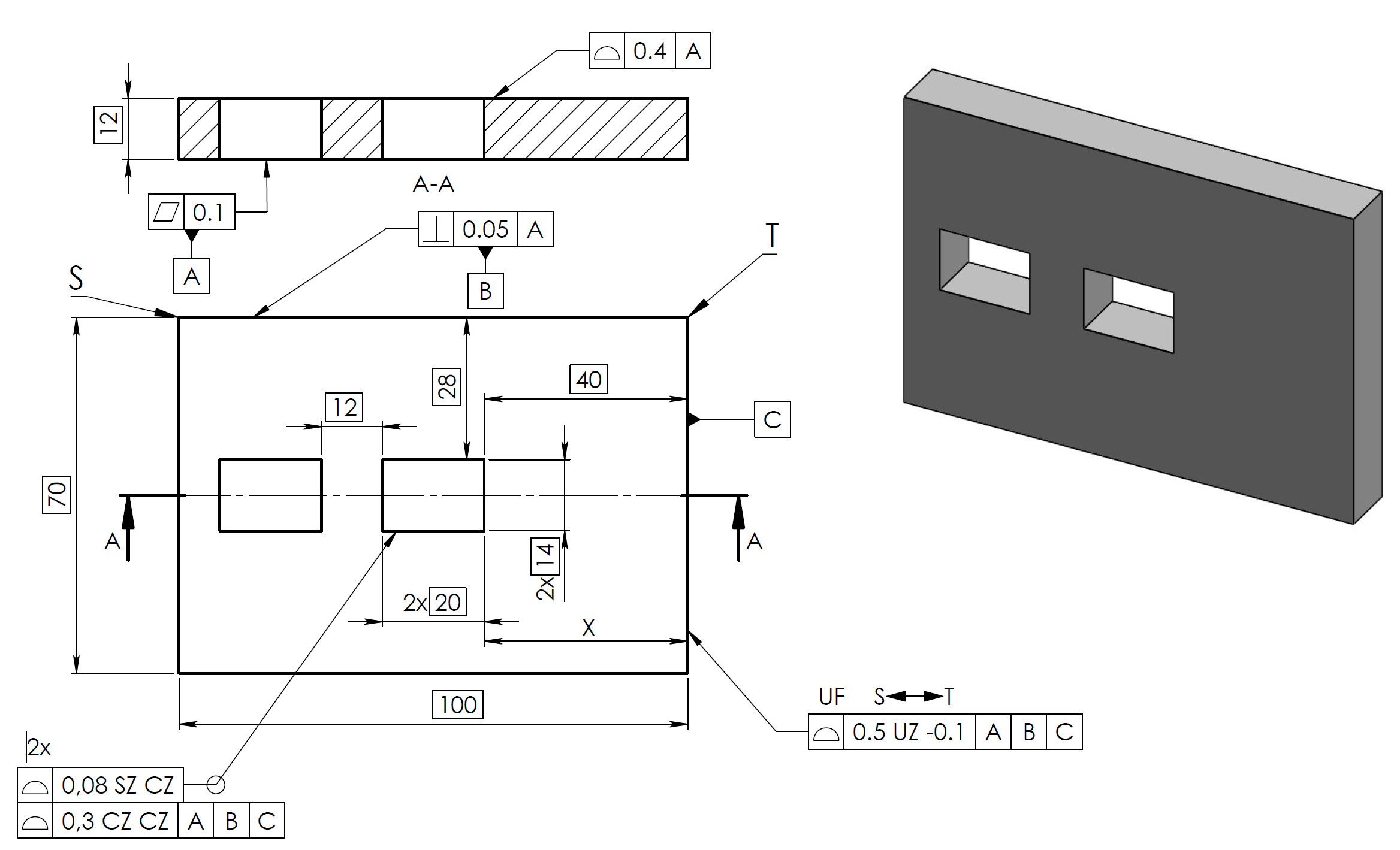
Questo ragionamento spiega anche i valori delle due quote funzionali del disegno di Figura 4, discussi nella prima parte, cioè la distanza X e le dimensioni limiti della lunghezza della piastra (quota nominale 100 mm). In corrispondenza del datum C, è disponibile solo la parte interna della tolleranza del profilo non simmetrica (+0.15/-0.35), per cui si ottengono i seguenti risultati:
Lunghezza L del componente (lunghezza nominale 100 mm):
Lmax = 100.15 mm Lmin = 99.3 mm
Le stesse considerazioni valgono per il calcolo della distanza X rispetto al riferimento C (distanza nominale 40 mm) che tiene conto della posizione del profilo della scanalatura (± 0.15):
Xmax= 40,15 mm Xmin= 39.5 mm