Un esempio di applicazione degli elementi monodimensionali

Nel precedente Quaderno di Progettazione abbiamo introdotto la teoria degli elementi monodimensionali, mostrando le varie formulazioni. In questa seconda puntata andremo a mostrare come modellare strutture composte da travature multiple e come creare le matrici di rigidezza dell’intera struttura.

di Franco Concli

Nel primo Quaderno di Progettazione dedicato al FEM è stato presentato il metodo degli Elementi Finiti (FE) con riferimento specifico alle formulazioni monodimensionali. L’approccio 1D, sebbene concettualmente semplice, rappresenta un passaggio essenziale per comprendere i principi alla base del metodo e per sviluppare familiarità con gli strumenti matematici e computazionali utilizzati.

L’uso di elementi lineari, le funzioni di forma e la formulazione debole del problema forniscono una base solida e spesso sufficiente per modellare sistemi anche complessi come, ad esempio, le strutture reticolari. L’impiego di questo approccio per la risoluzione di problemi reali in cui una sola dimensione domina il comportamento fisico (come barre, travi o condotti), semplifica molto la vita degli ingegneri ed è pertanto una pratica largamente diffusa. Vediamo alcuni esempi.

Applicazione degli elementi monodimensionali a strutture complesse

Nel primo Quaderno di Progettazione abbiamo ricavato la matrice di rigidezza per gli elementi barra e trave a partire dalle equazioni di equilibrio e congruenza.

Nel caso di strutture è necessario utilizzare più di un elemento finito per cui anche la matrice di rigidezza del sistema sarà data dalla combinazione delle matrici di rigidezza dei vari elementi che le compongono. Come facciamo riferimento ad una semplice struttura composta da tre elementi barra, compresi rispettivamente tra i punti 1 e 2 (el .1), 2 e 3 (el .2), 3 e 4 (el. 3); tali punti sono detti nodi della struttura.

Singoli elementi monodimensionali

I vettori degli spostamenti generalizzati d e delle forze generalizzate f relativi al primo elemento sono dati da k.

Tali vettori, però, fanno riferimento al sistema di riferimento locale dell’elemento e non al sistema di riferimento globale. Si rende dunque necessario un ulteriore passaggio che permetta di esprimere la matrice di rigidezza dell’elemento nel sistema di riferimento assoluto.

Ciò può essere fatto attraverso la matrice di rotazione R.

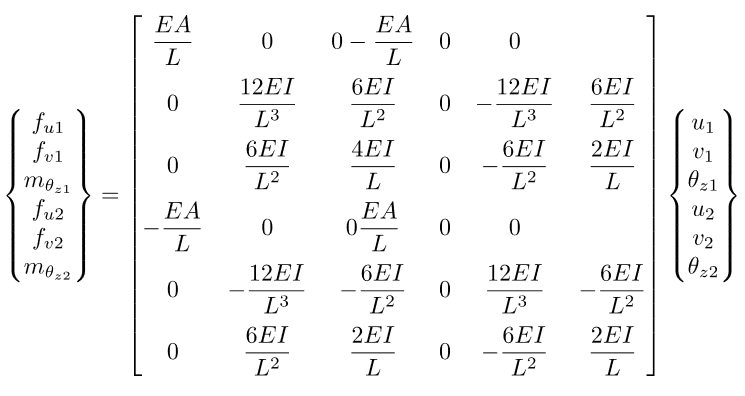
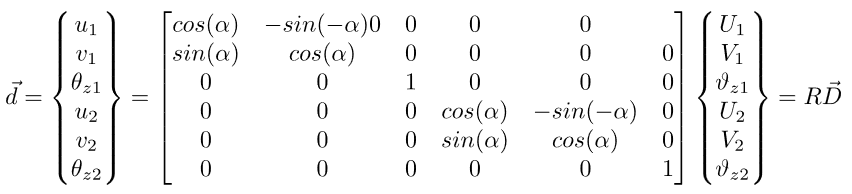
In questo caso la rotazione tra il sistema di riferimento relativo e quello assoluto vale .

Dopo le opportune trasformazioni:

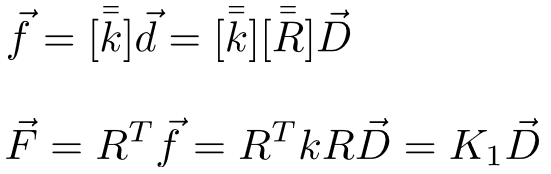
la matrice di rigidezza dell’elemento “el. 1 “nel sistema di riferimento globale K risulta:

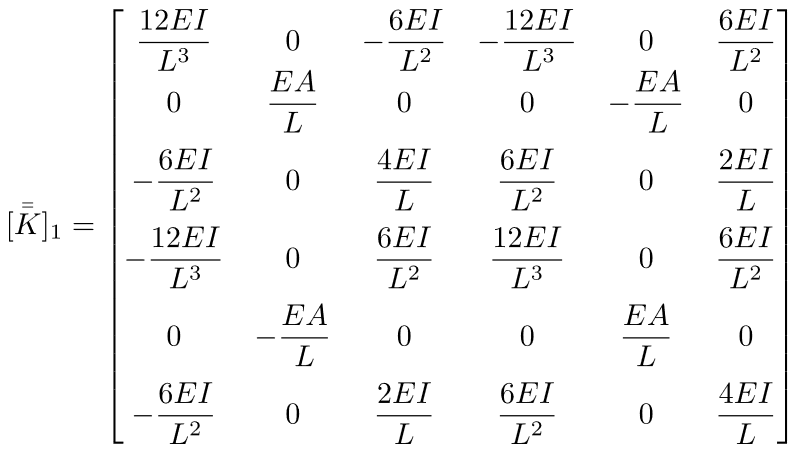
La stessa operazione può essere ripetuta per gli elementi finiti “el. 2” e “el. 3” che congiungono i nodi 2 a 3 e 2 a 4.

Strutture composte

Analogamente a quanto fatto per il singolo elemento, anche per la struttura vengono individuati due insiemi distinti di variabili:

• N variabili cinematiche, cioè gli spostamenti generalizzati (riferiti quindi al sistema di riferimento globale) necessari a definire il campo di spostamenti della struttura
• N variabili statiche, cioè forze generalizzate che dall’esterno sono applicate nei punti nodali della struttura

Il numero N di variabili cinematiche è dato dalla sommatoria, estesa a tutti i nodi della struttura – nell’esempio apri a 4 – del numero di gradi di libertà cinematici di ciascun nodo. Nel caso preso a titolo di esempio, dunque, il numero di gradi di libertà della struttura è pari a 16 (4×4).

Per ciascun nodo, è anche possibile scrivere

• un’uguaglianza tra le variabili cinematiche struttura e quelle degli elementi che concorrono nel nodo
• un equilibrio tra le variabili statiche struttura e quelle degli elementi che concorrono nel nodo

In generale, quindi, se alla struttura sono associate N variabili cinematiche ed N variabili statiche ed è composta da elementi che complessivamente comportano n variabili cinematiche e n statiche la descrizione delle connessioni tra i vari elementi della struttura porta a scrivere N equazioni di equilibrio ed n equazioni di congruenza. Tenendo conto che si hanno a disposizione altre n (una per ogni elemento) nella forma , totale si arrivano ad ottenere N + 2n equazioni risolutive del problema strutturale.

Per una risoluzione efficiente del sistema di equazioni e sistematicità del calcolo, risulta più conveniente una risoluzione a livello di struttura complessiva e non di singolo elemento. Questo viene implementato tramite il concetto di matrice di rigidezza complessiva K_G della struttura che altro non è che altro una matrice contenente le matrici di rigidezza K_i dei singoli elementi (convertite nel sistema di riferimento globale) ed opportunamente disposte in modo da rappresentare l’effettiva connessione tra i nodi.

Nel caso riportato come esempio, la matrice di rigidezza globale K_G risulterà

Come si nota nelle posizioni 1:3-1:3 (righe-colonne) si avranno solamente elementi appartenenti all’elemento 1 ( connesso al nodo 1). Nelle posizioni 4:6-4:6 si avranno sia elementi provenienti dall’elemento 1 () che dall’elemento 2 ().

Il fatto che in questo caso tutti gli elementi siano disposti sulle diagonali della matrice di rigidezza del sistema è legato alla particolare semplicità della struttura che prevede solamente un collegamento “sequenziale” tra gli elementi finiti.

Si noti inoltre che nel vettore globale dei carichi F_G si abbiano 6 incognite (in corrispondenza dei 6 gradi di libertà vincolati) nei nodi 1 e 4 mentre nel vettore degli spostamenti nodali della struttura D_G si abbiano 6 incognite corrispondenti agli spostamenti (e rotazioni) nodali dei nodi 2 e 3 (spostamenti e rotazioni dei nodi 1 e 2 sono nulli a causa dei vincoli).

Risoluzione

Il problema in esame è relativamente semplice da risolvere in quanto le equazioni (a seguito della specifica connessione tra i nodi) risultano in buona parte indipendenti. Pertanto è possibile separare la matrice di rigidezza K_G in due sottomatrici. La prima (K_G‘ ), che conterrà righe e colonne da 4 a 9 (ovvero quelle corrispondenti ai GDL per cui risulta le incognite sono gli spostamenti/rotazioni nodali), ed una (K_G“) che conterrà le righe e colonne da 1 a 3 e da 10 a 12 della matrice K_G (ovvero quelle corrispondenti alle reazioni vincolari incognite). Tali matrici potranno essere invertite in modo da ottenere i 6 spostamenti/rotazioni nodali e le 6 reazioni vincolari incognite.

In alternativa – cosa necessaria nel caso di strutture più complesse – la parte di risoluzione del problema viene lasciata agli algoritmi implementati nei vari codici FEM.

Esempio numerico

A titolo di esempio applicativo, prendiamo una struttura simile a quella vista nell’introduzione teorica ma costituita da 4 travi e non 3.

In questo caso, avendo 5 nodi, i gradi di liberà saranno 15.

Nel nodo 1 la struttura (in acciaio) è incastrata, mentre nel nodo 5 è supportata da una cerniera. Nel nodo 2 agisce una forza orizzontale F=10000N mentre nel punto 4 è applicato un momento M=-8kNm. 

Le lunghezze delle varie travi sono l₁₂ = 1875 mm, l₂₃ = 62.5 mm, l₃₄ = 1500 mm e l₄₅ = 2000 mm, il diametro è sempre pari a D = 60 mm.

Risoluzione numerica tramite inversione manuale delle matrici

Come si vede nella figura, gli elementi “el. 1” ed “el. 2” sono ruotati di 90 gradi rispetto al sistema di riferimento assoluto mentre l’elemento “el. 4” è ruotato di -90.

Di conseguenza è necessario effettuare una trasformazione delle relative matrici di rigidezza nel sistema di riferimento locale k_i in quello assoluto (K_i).

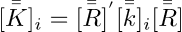
A questo punto è possibile assemblare la matrice di rigidezza complessiva del sistema che risulterà diagonale.

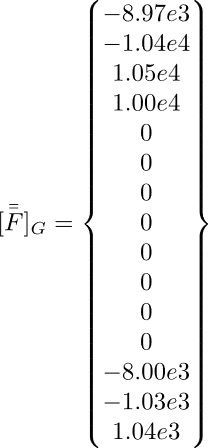
Applicando la tecnica di separazione della matrice in righe e colonne in cui le variabili sono gli spostamenti e righe e colonne in cui le variabili sono le reazioni vincolari è possibile arrivare alla seguente soluzione

Risoluzione numerica tramite software FEM open-source Calculix

In questa sezione mostreremo come modellare il problema di cui sopra mediante il software open-source Calculix. Calculix è un software multipiattaforma composto da un solutore (CCX) ed un visualizzatore grafico (CGX). Il settaggio delle simulazioni avviene mediante script. Recentemente è stato anche sviluppato un ambiente grafico (PrePoMax) che permette la generazione tramite interfaccia di tali script di comando. Tuttavia, è importante comprendere il linguaggio e la struttura di tali script. Per questo, in questo Quaderno di Progettazione andremo a vedere nel dettaglio le linee di codice necessarie per settare la simulazione. Nei prossimi Quaderni di Progettazione mostreremo anche il funzionamento dell’interfaccia PrePoMax (utile nel caso sia necessario settare simulazioni più comlpesse).

La definizione dei nodi è possibile mediante la keyword (o scheda) *NODE. Vengono definite le posizioni dei 5 nodi nel sistema di riferimento cartesiano assoluto.

Definiti i nodi è necessario “collegarli” con gli elementi finiti (con la scheda *ELEMENT). Il tipo *B21 fa riferimento ad elementi trave (beam) bidimensionali (2) lineari (1).

La definizione del materiale avviene con la scheda *MATERIAL ed i valori richiesti sono il modulo elastico (210000) e il coefficiente di Poisson (0.3).

In questo modo è stato creato un materiale ma è anche necessario assegnarlo ai vari elementi finiti (assieme alla loro sezione). Ciò avviene tramite la scheda *BEAM SECTION

In questo caso a tutti gli elementi del set “Frame” definito nella scheda *ELEMENR viene assegnato il materiale “steel” definito nella scheda *MATERIAL. Inoltre viene specificata la sezione delle travi (sezione rettangolare 6x6mm).

La definizione delle reazioni vincolari avviene nella scheda *BOUNDARY

Il primo numero è l’ID del nodo in accordo a quanto definito nella scheda *NODE mentre il secondo ed il terzo numero rappresentano i gradi di libertà (GDL) da vincolare. 1,3 significa che tutti i GDL da 1 a 3 (u_x, u_y, θ_z) sono bloccati.

I carichi sono applicati in modo analogo mediante la scheda *CLOAD (i.e. concentrated load).

In questo caso il primo numero rappresenta il GDL, il secondo il valore del carico.

Infine, è necessario definire il tipo di analisi (statica in questo caso) e gli elementi che si desiderano avere in output (in questo caso gli spostamenti U e le reazioni vincolari RF).

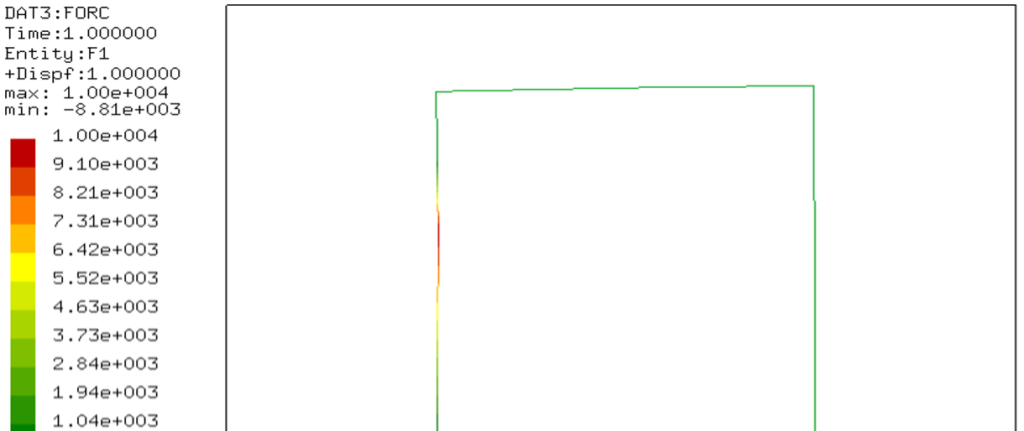
Nella figura sono plottate le reazioni vincolari in direzione x (F₁). Di vede come nel nodo 2 il valore corrisponda alla forza F applicata mentre nel nodo 1 il valore sia uguale a quello calcolato mediante inversione delle matrici per la reazione reazione vincolare R₁=8.9e3.

Conclusioni

In questo secondo appuntamento dedicato agli elementi finiti abbiamo mostrato un primo esempio di applicazione degli elementi finiti, tramite il software open-source Calulix, per il calcolo di una semplice struttura. Nella prossima puntata introdurremo gli elementi piani.