Questo lavoro riassume uno studio comparativo relativo all’accuratezza dei criteri per la previsione della vita a fatica a basso numero di cicli per un acciaio AISI 316L. Varie serie di provini sono state testate in condizioni di deformazione controllata. I livelli di sollecitazione e deformazione sviluppati durante un ciclo di fatica di prova sono stati calcolati attraverso un modello ad elementi finiti una volta nota la curva ciclica. Successivamente, sono stati valutati quattro diversi criteri di previsione della vita basati sulle deformazioni e sulla teoria del piano critico, vale a dire il criterio di Smith-Watson-Topper, il criterio di Fatemi-Socie e i due criteri di Chen-Xu-Huang.
di Lorenzo Pagliari e Franco Concli
Quando i componenti subiscono carichi che si ripetono nel tempo, possono verificarsi cedimenti per fatica. La fatica è il fenomeno per cui un materiale soggetto a carichi ciclici, ceda anche per carichi inferiori a quelli che portano ad una rottura statica, e rappresenta una delle cause più frequenti di cedimento dei sistemi meccanici [1]. Si verifica poiché a livello microscopico si manifesta una intensificazione delle sollecitazioni dovuta, ad esempio, a difetti superficiali. Tali sollecitazioni risultano sufficienti a causare una deformazione microscopica localizzata, anche se le sollecitazioni a livello macroscopico rimangano in campo elastico [2]. Poiché i carichi si ripetono ciclicamente, il danneggiamento può propagare in profondità nel materiale. Questo si verifica spesso con pochissimi o nessun segnale di preavviso, causando infine un cedimento improvviso [2]. Quando i carichi ciclici applicati comportano sollecitazioni che non superano mai il limite di snervamento, si parla di fatica ad alto numero di cicli, High-Cycle Fatigue (HCF). In condizioni di HCF i materiali subiscono deformazioni essenzialmente solo elastiche. Si noti che questo è valido a livello macroscopico, mentre nelle regioni microscopiche sopra menzionate (le più importanti delle quali sono gli apici delle cricche che poi propagano) si avrà comunque una deformazione plastica.
Poiché l’HCF, almeno a livello macroscopico, comporta solo deformazioni elastiche, il numero di cicli necessari per raggiungere la rottura in queste condizioni risulta relativamente elevato. Tipicamente, varia tra 103 e 107 cicli [3]. Quando l’intensità dei carichi applicati è tale da comportare sollecitazioni che superano la resistenza allo snervamento del materiale, si parla invece di fatica a basso numero di cicli, Low-Cycle Fatigue (LCF). In condizioni di LCF le deformazioni plastiche cicliche si hanno anche a livello macroscopico [4]. Pertanto, per un dato materiale, le condizioni di carico LCF risultano sempre più severe di quelle HCF e la durata di un componente soggetto a LCF risulta inevitabilmente più contenuto rispetto alle condizioni HCF. La vita LCF per i metalli varia da 102 a 10, 3 – 104 cicli [5-7]. Le applicazioni industriali in cui la fatica LCF deve essere presa in considerazione in fase di progettazione coprono un’ampia gamma di applicazioni, che spaziano dal settore automobilistico [4, 8], alla produzione di motori a turbina [9, 10], dal settore delle costruzioni civili [11, 12], alla produzione di energia nucleare [14, 13]. Vi sono anche esempi di cedimenti a LCF anche nei settori dell’estrazione petrolifera [15, 16] e nel settore navale/marittimo [17, 18]. Alla luce della rilevanza delle applicazioni soggette a LCF, risulta chiaro come essere in grado di prevedere la durata di un componente soggetto a deformazioni plastiche cicliche sia una sfida di fondamentale importanza industriale. Per questo motivo, negli anni sono stati sviluppati molteplici criteri. Questi elaborano le sollecitazioni e le deformazioni cui il materiale è sottoposto durante l’esercizio, in modo da calcolare un parametro di danneggiamento che possa poi essere correlato alla durata a fatica. Revisioni dettagliate possono essere trovate nei lavori di Luo et al. [19], Carpinteri et al. [20] e Zhong e Lu [21]. Tra i criteri LCF disponibili, quelli che si basano sulla teoria del “piano critico” consentono di trovare sia il punto di innesco della cricca che il suo orientamento. Questi criteri funzionano identificando il piano in cui una certa combinazione di sollecitazioni e deformazioni risulta massima. Tale piano è quindi assunto come il piano in cui il danneggiamento a fatica risulta massimo, e viene quindi chiamato “piano critico” [22]. La combinazione di componenti di sollecitazione/deformazione dipende dal criterio specifico impiegato. Il punto materiale in cui si trova il piano più critico è il punto in cui si prevede che nuclei la cricca e la direzione di quel piano è la direzione prevista per le prime fasi della propagazione. I criteri basati sul piano critico sono generalmente apprezzati per la loro buona precisione predittiva, per la grande varietà di materiali e applicazioni a cui possono essere applicati e per la loro efficacia nell’identificare l’orientamento della cricca [31-34]. Sono spesso utilizzati in combinazione con l’analisi numerica e le simulazioni FEM (Finite Element Method) [22-26].
Lo scopo di questo lavoro è quello di valutare l’accuratezza dei quattro principali criteri basati LCF basati sulla teoria del piano critico. Nello specifico, i criteri analizzati sono quelli sviluppati da Smith et al. [35], Fatemi e Socie [36] e Chen et al. [37] (due criteri). Lo studio ha preso come materiale di riferimento un acciaio AISI 316L. Ai provini è stato applicato un carico assiale ciclico (trazione) ed è stato misurato il numero di cicli necessari per fare nucleare una cricca. La stessa procedura sperimentale è stata simulata in ambiente FEM, calcolando i tensori di deformazione e di sforzo, elaborati poi attraverso i criteri sopra citati. L’efficacia dei criteri è stata valutata confrontando il numero di cicli per la nucleazione della cricca previsti (sulla base della previsione FEM + criterio) con i valori osservati sperimentalmente. Nella prima parte di questo lavoro vengono presentati i quattro criteri oggetto di analisi e il loro i principi di funzionamento. Nella seconda parte viene descritta la procedura sperimentale, mentre nella terza vengono spiegate la simulazione FEM e l’analisi numerica condotte per valutare la storia di carico. Nella quarta parte vengono presentati e commentati i risultati, prima di trarre le conclusioni e di delineare gli sviluppi futuri.
Criteri basati sul concetto di piano critico
Come accennato in precedenza, questo lavoro valuta l’efficacia di quattro diversi criteri di fatica a basso numero di cicli basati sull’analisi della deformazione attraverso approcci con definizione di un piano critico. In questa sezione vengono descritti i criteri e i relativi principi di funzionamento.
Smith, Watson e Topper (SWT)
Il criterio di Smith, Watson e Topper (criterio SWT) era inizialmente applicabile solo alla fatica uniassiale [35], fino a quando Socie lo ha successivamente esteso alle sollecitazioni cicliche multi-assiali [38]. Il criterio assume che il piano critico sia il piano caratterizzato dall’intervallo massimo di deformazione normale (∆εn,max) e che la cricca nuclei appunto su tale piano. Di conseguenza, per trovare tale piano risulta necessario calcolare l’intervallo di deformazione per ogni ipotetico piano passante per ogni punto appartenente al componente da analizzare. Questo può essere meglio compreso osservando la Fig.1 che mostra un generico piano passante per un punto indefinito (detto i-esimo piano), avente come coordinate sferiche φ e θ. Siano, inoltre, X’Y’Z’ un nuovo sistema di coordinate solidale all’i-esimo piano, ε’x(t) la deformazione normale, mentre γ’xy(t) e γ’xz(t) le deformazioni angolari su tale piano. I loro valori variano nel tempo e per questo si arriva ad un cedimento per fatica. L’intervallo di deformazione dell’i-esimo piano è calcolato come segue:
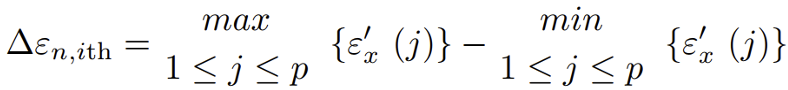
in cui p è il numero di step in cui sono stati suddivisi i cicli di carico. Tale calcolo deve essere eseguito per ogni pianoi-esimo e per ogni punto discreto del componente in analisi. Il massimo valore ∆εn,ith che si trova viene indicato come ∆εn,max, mentre il punto e il piano che lo caratterizza sono rispettivamente detti punto e piano critici. Una volta trovato ∆εn,max, la durata fatica può essere determinata attraverso la relazione di Basquin-Coffin-Manson:
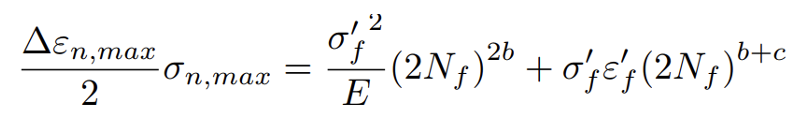
Fatemi e Socie (FS)
Il criterio di Fatemi e Socie (criterio FS) [36] si basa sull’ipotesi che le cricche nucleino sui piani di massimo intervallo della deformazione di taglio (∆γmax), identificati quindi come i piani critici. Inoltre, il criterio di FS utilizza la sollecitazione perpendicolare al piano come parametro di danneggiamento secondario che promuove la propagazione della cricca. Di conseguenza, per trovare il piano critico è necessario calcolare l’intervallo di deformazione di taglio per ogni i-esimo piano passante per ogni punto del componente in analisi. Facendo riferimento alla Fig.1, ∆γith può essere calcolato come [28]:
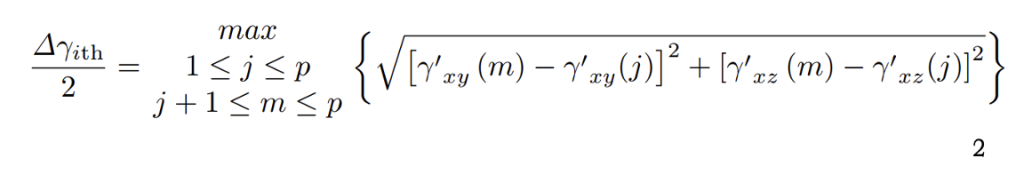
La variazione massima di ∆γithviene indicata come ∆γmax, mentre il punto e il piano che lo caratterizzano sono rispettivamente il punto e piano critici. Una volta trovato ∆γmax, questo può essere collegato alla vita a fatica attraverso la relazione di Basquin-Coffin-Manson:
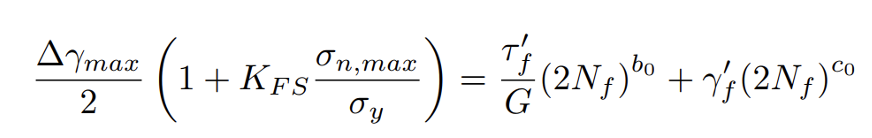
e c0 è l’esponente di duttilità a taglio. KFS è un coefficiente di adattamento dei dati che può essere calcolato come [39]:
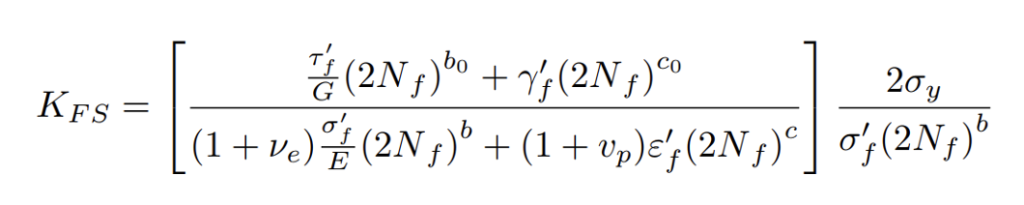
Chen, Xu, Huang (CXH I, CXH II)
Chen et al. [37] hanno proposto due criteri basati sul concetto di piano critico, i cosiddetti criteri CXH I e CXH II. Il criterio CXH I consiste in una modifica di quello inizialmente proposto da SWT, in cui, quindi, il piano critico è identificato come il piano che presenta il massimo intervallo di deformazione normale (∆εn,max). Il criterio integra il parametro di danneggiamento di SWT aggiungendo però il contributo della sollecitazione di taglio e della deformazione di taglio sul piano critico:
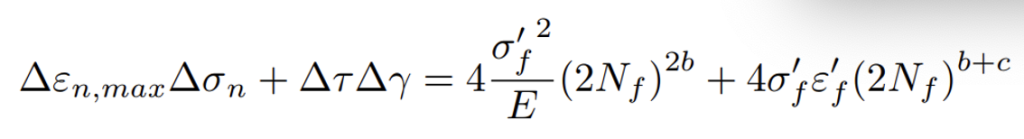
dove ∆σn, ∆τ e ∆γ sono gli intervalli della sollecitazione normale, della sollecitazione di taglio e della deformazione angolare calcolate sul piano critico.
Il criterio CHX II identifica il piano critico come quello avente il più ampio intervallo di deformazione angolare (∆γmax). In questo caso integra il contributo della sollecitazione normale e della deformazione normale sul piano critico:
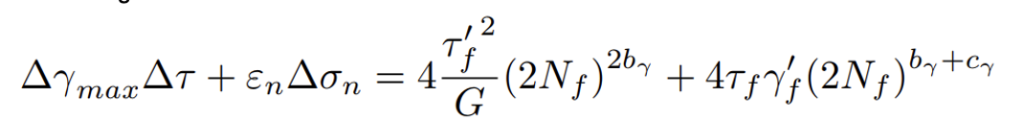
Anche in questo caso ∆σn, ∆τ e ∆εn sono calcolati sul piano critico.
Prove sui materiali:
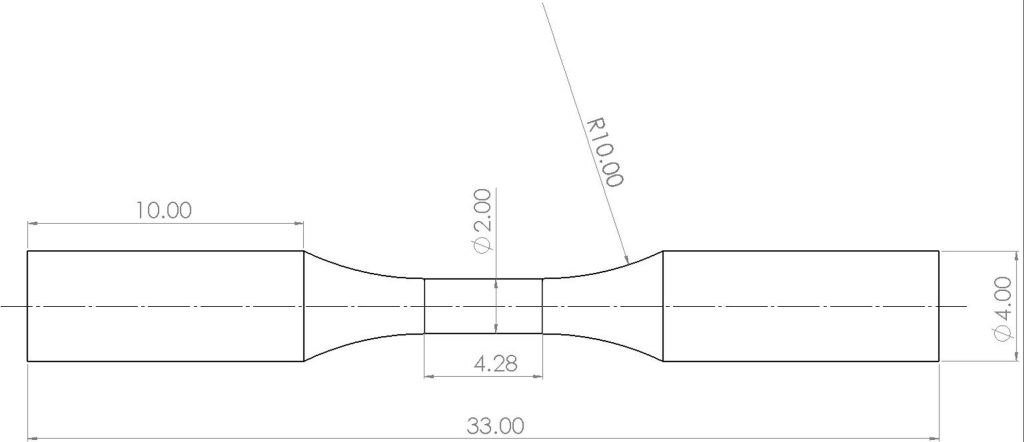
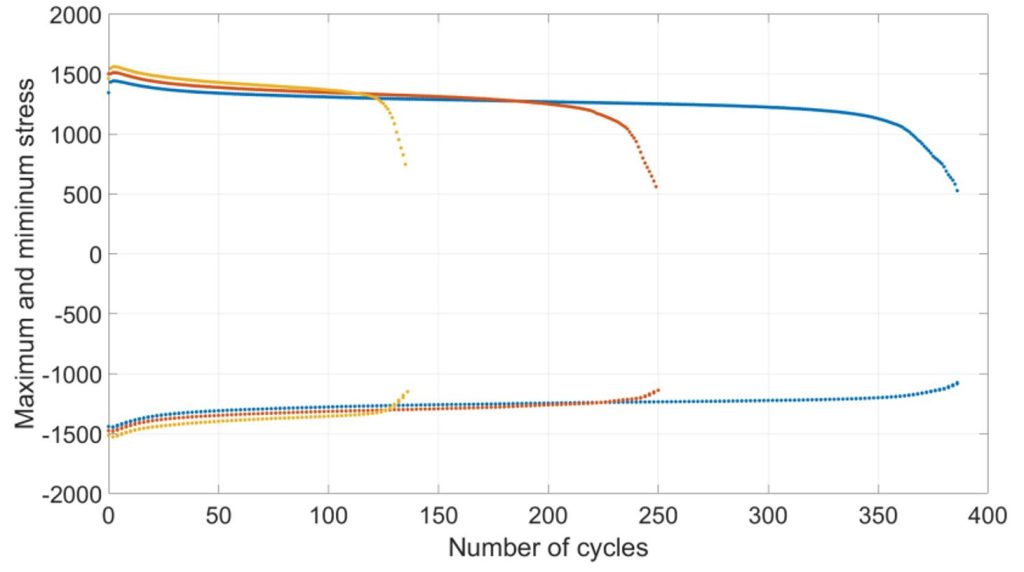
I provini in AISI 316L sono stati fabbricati e testati secondo lo standard ASTM-E606 [41], ottenendo le proprietà a fatica e le caratteristiche del materiale riportate in Tabella 1. Seguendo le stesse procedure standardizzate, sono stati prodotti tre provini in AISI 316L da testare in prove a deformazione controllata. La loro geometria è illustrata in Fig.2. Ogni provino è stato testato con un diverso livello di deformazione imposta, come mostrato nella tabella 2. Tutte le deformazioni sono state applicate in direzione assiale con rapporto ciclo R = -1. La Fig.3 mostra i carichi massimi e minimi osservati nei tre test. Come si può osservare, il materiale ha mostrato un incrudimento solo nei primissimi cicli, e poi un rammollimento fino alla stabilizzazione, in accordo quanto riportato in letteratura per questo materiale [29, 30,]. Un comportamento simile è stato ottenuto per tutti i campioni testati. La Tabella 2 riporta il numero di cicli in condizioni cicliche stabilizzate a cui i vari provini sono stati sottoposti (come descritto da Ramberg e Osgood [40]), il numero di cicli a nucleazione e quello a cedimento.


Modellazione FEM ed applicazione dei criteri:
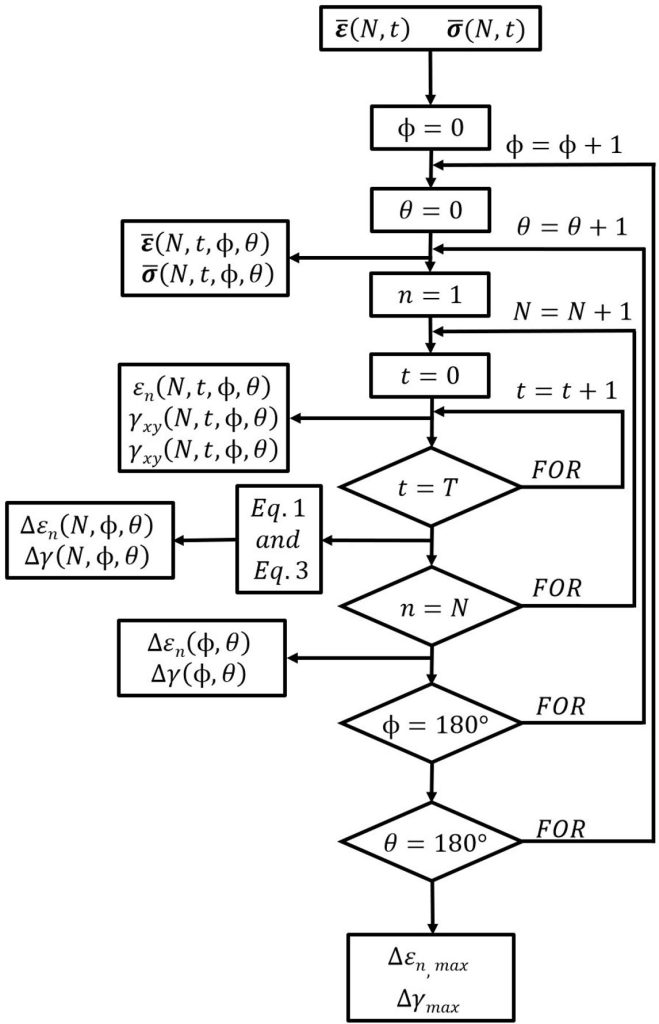
La procedura sperimentale descritta nella sezione precedente è stata simulata attraverso un software FEM open-source (nello specifico Salome-Meca/Code_Aster). In tale ambiente, la geometria dei campioni è stata riprodotta fedelmente e le proprietà meccaniche modellate secondo la legge di Ramberg-Osgood (K’ e n’). Si noti che numericamente si è simulato tutto considerando il materiale stabilizzato già a partire dal primo ciclo di carico. Di conseguenza, quando i risultati delle simulazioni sono stati utilizzati come input per l’applicazione dei criteri di fatica LCF, la previsione della vita è stata correlata alla parte stabilizzata delle curve sperimentali. In altre parole, si è scelto di valutare l’accuratezza dei criteri confrontando la vita prevista con il numero di cicli stabilizzati. È stato simulato un ciclo di carico per ciascuna delle tre deformazioni cicliche descritte nella Tabella 2. I tensori di sollecitazione e deformazione sono stati quindi esportati e hanno potuto essere elaborati con i quattro criteri di fatica. La Fig.4 mostra la procedura numerica generale che è stata seguita.
Per ogni valore discreto degli angoli ϕ e θ (Fig.1) compreso tra 0° e 180°, per ogni nodo n della mesh di calcolo FEMe per ogni istante di tempo t, i tensori di sollecitazione e deformazione ((n,t) e
(n,t)) sono stati convertiti a seconda del sistema di riferimento locale del piano i-esimo (definito da ϕ e θ). In questo modo è stato possibile determinare i valori istantanei della deformazione normale e delle deformazioni di taglio sul piano in esame e la posizione specifica (i.e. nodo corrente) (ε‘n(n,t, ϕ,θ), γ‘xy(n,t, ϕ,θ), γ‘xz(n,t, ϕ,θ)).
Dopo aver calcolato ε‘n (n, ϕ,θ), γ‘xy(n, ϕ,θ) e γ‘xz(n, ϕ,θ), il piano corrente e il nodo corrente possono essere trovati rispettivamente attraverso l’equazione 1 e l’equazione 3.
Il calcolo viene ripetuto per tutti gli N nodi della mesh, determinando così gli intervalli di deformazione per l’intero piano corrente.
Gli intervalli di deformazione sono calcolati per tutti i valori di ϕ e θ compresi tra 0° e 180°, ad intervalli incrementali di 1°. A valle di questa fase, gli intervalli di deformazione risultano determinati per ogni nodo e ogni piano, e si possono trovare l’intervallo di deformazione normale massimo ε‘n,max (per i criteri SWT e CHXI) e/o l’intervallo di deformazione angolare massimo γ‘max (per i criteri FS e CHXII).
Oltre agli intervalli di deformazione massima ε‘n,max e γ’max, i criteri richiedono altri parametri, quali la sollecitazione normale massima (criteri SWT e FS), l’intervallo della sollecitazione normale (criteri CHX I e CHX II), l’intervallo della deformazione normale (criterio CHX II), l’intervallo della sollecitazione di taglio (criteri CHX I e CHX II) e l’intervallo della deformazione di taglio (criterio CHX I), (Eq. 2, Eq. 4, Eq. 6 ed Eq. 7).
Risultati:
Gli orientamenti delle cricche previsti dai criteri riflettono il tipo di principio di funzionamento su cui questi si fondano. I criteri SWT e CHX I, che identificano il piano critico come il piano avente il massimo intervallo di deformazione normale, hanno identificato il piano critico come normale all’asse del provino. Nel caso dei criteri FS e CHX, il piano critico previsto è risultato essere inclinato di 45° rispetto all’asse del provino. Ciò è in relazione al fatto che tali criteri identificano il piano critico come il piano avente il massimo intervallo di deformazione di taglio.
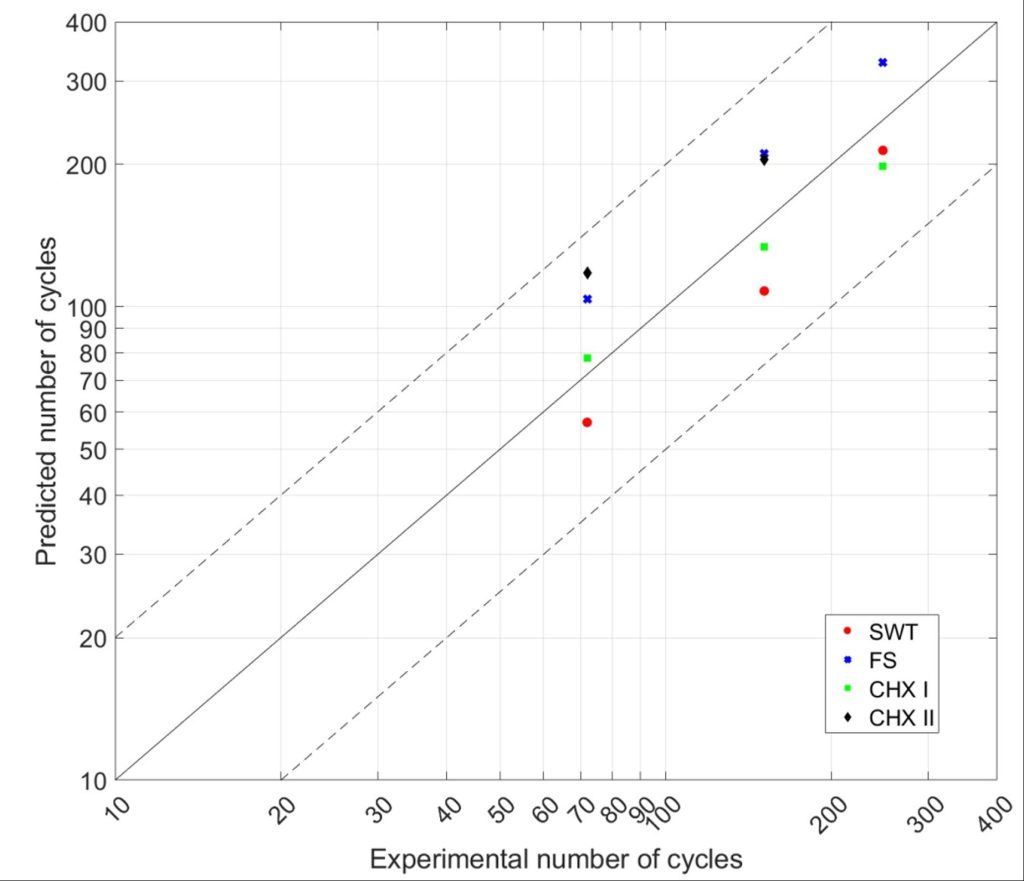
Per quanto riguarda il numero di cicli previsti da ciascun criterio per ciascun campione, si faccia riferimento a Tabella 3 (in cui viene riportato anche il numero di cicli stabilizzati osservato sperimentalmente). Osservando Fig.5 si può osservare come i modelli basati sull’identificazione del piano di massima deformazione normale (criteri SWT e CHX I) producono previsioni conservative e generalmente accurate. Il criterio SWT risulta il più conservativo tra i due. Al contrario, i modelli basati sull’identificazione del piano di massima deformazione angolare (criteri FS e CHX II) tendono a sovrastimare la vita a fatica e ad essere meno accurati. Questo comportamento è particolarmente esacerbato nel caso del criterio CHX II. Va precisato come la mancanza di accuratezza dei modelli FS e CHX II non è da attribuirsi ad una loro inefficacia in senso assoluto, ma al fatto che, essendo basati sull’identificazione del piano di massimo taglio, danno buoni risultati solo quando si hanno prevalentemente carichi di natura torsionale. Un caso di carico puramente assiale rappresenta una condizione in cui in realtà non dovrebbero essere in grado di produrre una previsione accurata.

Conclusioni:
Tre campioni di AISI 316L sono stati testati in condizioni di fatica a basso numero di cicli in condizioni di deformazione controllata. I livelli di sollecitazione e deformazione agenti durante un ciclo di carico sono stati calcolati attraverso un modello ad elementi finiti e analizzati utilizzando i criteri SWT, FS, CHXI e CHX II. Per ognuno di essi è stata ottenuta una previsione di vita. Confrontando i risultati sperimentali e numerici, è stato osservato come l’accuratezza dei criteri basati sulla deformazione vari a seconda del principio di funzionamento su cui si basano. Il criterio SWT fornisce risultati conservativi ma abbastanza accurati, mentre il criterio FS è meno accurato e tende a sovrastimare la vita. Tali comportamenti opposti sono in accordo con precedenti ricerche sugli acciai della famiglia AISI 316 [42]. Per quanto riguarda i modelli CHX I e CHX II, il primo porta a risultati conservativi e più accurati di quelli del criterio SWT, mentre il secondo fornisce previsioni ancora meno accurate e più sovrastimate rispetto al modello FS. Anche per questi due criteri un comportamento simile è allineato con i risultati di ricerche precedenti su acciai della famiglia AISI 316 [43]. La mancanza di accuratezza dei modelli FS e CHX II è da attribuirsi al fatto che questi sono criteri che danno buone previsioni in presenza di carichi torsionali predominanti. Gli autori hanno in programma di approfondire ulteriormente i criteri analizzati in questo lavoro attraverso un’ampia campagna sperimentale, estendendo l’analisi ad altri criteri, agli stati multi-assiali e a condizioni di carico complesse, e.g. ampiezza non proporzionale e variabile.