La modellazione dei contatti nelle analisi agli elementi finiti

Un cosiddetto “problema di contatto” è classificabile come una non linearità al contorno, in cui sia lo spostamento, sia la forza di contatto sono incognite del problema.

A differenza di altri tipi di simulazione in cui alcuni nodi della mesh del componente sono sottoposti ad un carico noto, nella simulazione di contatto sia la posizione del contatto (e quindi il set di nodi), sia il valore del carico sono sconosciute.

Con un’analisi dei contatti è possibile determinare:

•          Se due o più corpi sono in contatto

•          La regione di contatto

•          La forza di contatto o pressione all’interfaccia

•          Se all’interfaccia è presente un movimento relativo dopo il contatto

La procedura FEA per un problema di contatto prevede due fasi principali:

•          Valutazione della sussistenza di un contatto

•          Nel caso un contatto sia presente, determinazione della forza di contatto corrispondente

Trovare l’equilibrio del sistema implica trovare un campo di spostamento che minimizzi l’energia potenziale. Questa minimizzazione è limitata dalle condizioni di contatto, il che significa che la soluzione deve soddisfare ulteriori restrizioni geometriche e/o meccaniche.

Numericamente, questo problema può essere risolto utilizzando il metodo della penalizzazione, che approssima i vincoli attraverso una rigidezza fittizia, oppure mediante il metodo del moltiplicatore di Lagrange, che introduce variabili ausiliarie per imporre i vincoli in modo esatto.

I problemi di contatto sono onerosi dal punto di vista computazionale per varie ragioni.

La prima è legata al fatto che la reale area di contatto è sconosciuta: la vera zona di contatto non è nota a priori, ma deve essere determinata come parte stessa della soluzione. Sebbene spesso sia possibile identificare una zona massima in cui il contatto avverrà e, dunque, limitare la ricerca a quella zona, la accuratezza con cui l’area viene determinata dipende dalla convergenza iterativa.

La seconda causa è legata ad una risposta discontinua della forza: le forze di contatto, infatti, mostrano cambiamenti bruschi (ad esempio, da zero ad un valore finito quando le superfici si toccano). Questa discontinuità assomiglia ai vincoli di incomprimibilità, che richiedono metodi specializzati (moltiplicatori di Lagrange o metodi di penalità)

La terza va individuata nella sensibilità discreto al contorno: nei modelli numerici, l’area di contatto evolve da nodo a nodo e non in modo uniforme come nella teoria del continuo. Ciò rende i risultati altamente sensibili alla discretizzazione (dimensione della mesh).

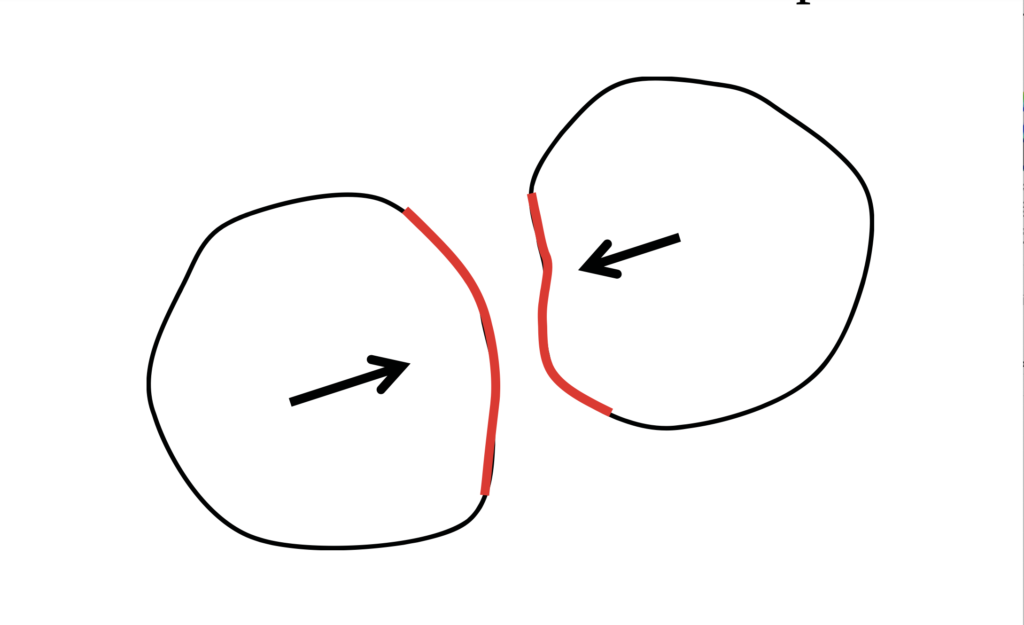
1. Approcci di risoluzione

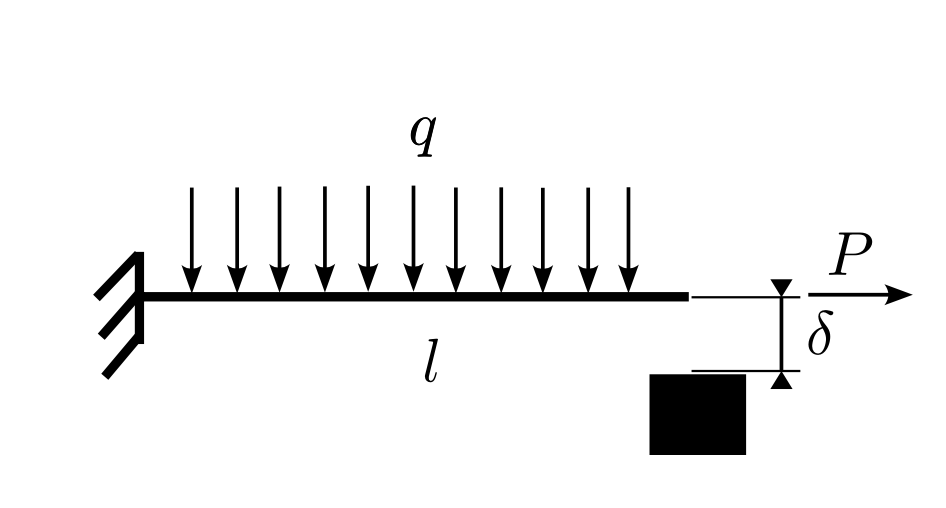
Si consideri una trave a sbalzo sottoposta ad un carico distribuito che entri in contatto con una superficie rigida. Il sistema è caratterizzato da un carico distribuito q = 1 kN/m agente sulla trave di lunghezza L = 1m con rigidezza flessionale EI = 105Nm². La deflessione massima consentita è pari a δ=1mm.

Ci sono tre approcci principali per risolvere il problema: soluzione per tentativi (trial and error), moltiplicatore di Lagrange o metodo della penalizzazione.

1.1. Soluzione per tentativi

La deflessione della punta di una trave a sbalzo sottoposta ad un carico distribuito è data da:

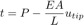
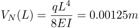
Quando la deflessione della punta V_N(L) supera la distanza consentita δ=1mm, si verifica il contatto con la superficie rigida. Ciò richiede l’introduzione di una forza di reazione verso l’alto λ agente sulla punta della trave in modo da impedire la compenetrazione. Il contributo alla deflessione di questa forza di reazione è descritto da:

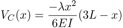
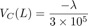
Di conseguenza, la forza λ necessaria ad impedire la compenetrazione può essere calcolata imponendo impostando V_tip=δ.

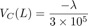
Da cui λ = 75N.

È possibile trattare sia la forza di contatto, sia la distanza come sconosciute

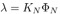
e aggiungere vincoli. In particolare, sono tre gli stati distinti che caratterizzano il comportamento del sistema. Innanzitutto, quando V_N(L)<δ, non si verifica alcun contatto per cui λ=0. Il contatto attivo (λ>0) richiede la condizione V_tip=δ. La terza condizione è rappresentata dal caso fisicamente inammissibile di λ<0 che implicherebbe una reazione di trazione al vincolo esterno. La funzione gioco g=V_tip−δ deve soddisfare g≤0 per impedire la penetrazione, con valori positivi di g che rappresentano valori non fisici .

1.2. Moltiplicatore di Lagrange

Per l’esempio precedente, la condizione di contatto prevedeva:

•          Nessuna penetrazione (g ≤ 0)

•          Forza di contatto positiva (λ ≥ 0)

•          Condizione di consistenza (λg = 0)

Il moltiplicatore di Lagrange può essere descritto come una strategia matematica per trovare i massimi e i minimi locali di una funzione soggetta a vincoli. λg risulta infatti

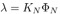
Quando λ=0N → g=0.00025>0 → viene violata la condizione di contatto.

Quando λ=75N → g = 0 → la condizione di contatto risulta soddisfatta.

1. 3. Metodo di penalizzazione

Nel metodo della penalizzazione, è ammessa una piccola penetrazione tra le parti. La forza di contatto risulta proporzionale ad essa. La funzione di penetrazione è definita come:

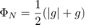
che risulta pari a 0 quando g≤0 (nessun contatto) e pari a g quando g>0 (contatto). La forza di contatto è definita come

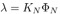
dove K_N è il parametro di penalizzazione (una sorta di rigidezza).

Da  si ha

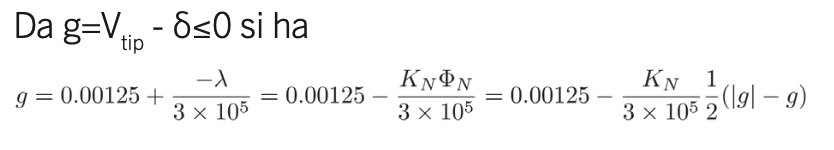
Sembra dunque che il divario dipenda dal parametro della penalità.

Tabella 1: risultati in funzione del parametro di penalizzazione scelto

KN	Penetrazione (-g) [m]	Forza di contatto (λ) [N]

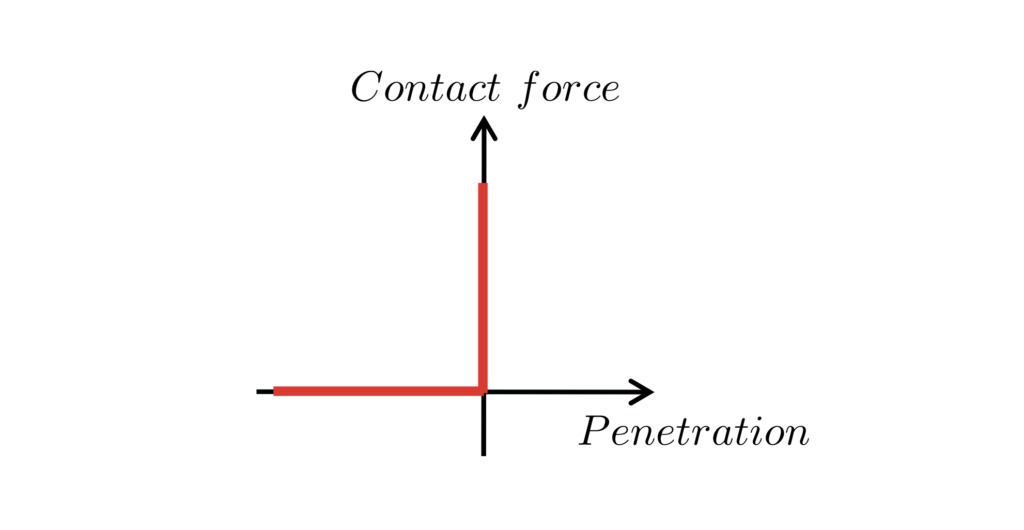
I risultati numerici mostrano il comportamento caratteristico del contatto (forza e compenetrazione) al variare del parametro di penalizzazione: all’aumentare del parametro di penalizzazione K_N, la penetrazione fisica −g diminuisce, seguendo la relazione inversa −g≈ λ/K_N, mentre la forza di contatto λ converge verso la soluzione esatta. Questo illustra la necessita di trovare un compromesso ideale per l’impiego dei metodi di penalizzazione: valori elevati di K_N applicano la regola di “non penetrazione” in modo più rigoroso fornendo dunque soluzioni accurate. Tuttavia, valori eccessivi rendono i calcoli più complessi. Al contrario, valori eccessivamente piccoli mantengono i calcoli più semplici ma consentono una maggiore penetrazione (effetto non fisico).

2. Attrito

In alcuni casi, è anche interessante capire se esista un movimento relativo tra i corpi a contatto. Per questo motivo, dopo aver applicato una forza q, la stessa trave a sbalzo dell’esempio precedente viene caricata assialmente anche da una forza concentrata P=100N applicata all’estremità di destra. Si presume che il coefficiente di attrito sia μ=0.5.

2.1 Soluzione per tentativi ed errori

In caso di assenza di attrito, l’applicazione della forza P induce uno spostamento assiale dell’apice della trave.

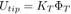
Il vincolo ulteriore dato dall’attrito può essere espresso come:

•          Condizione di adesione se t−μλ<0, U_tip=0

•          Condizione di scorrimento se t−μλ=0, U_tip>0

•          Condizione di consistenza U_tip(t-μλ)=0

in cui t è la forza di attrito tangenziale.

Per prima cosa valutiamo la condizione di adesione

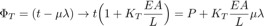
Avere t=100N viola la condizione di adesione t−μλ<0. Da questo è possibile dedurre che vi sarà dello scorrimento.

Sapendo che λ=75N, t potrebbe essere calcolato come t=μλ=37.5N.

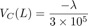
Questa soluzione soddisfa la condizione di scorrimento U_tip>0 e, pertanto, è una soluzione valida.

2.2 Moltiplicatore di Lagrange

In questo caso viene utilizzata la condizione di consistenza U_tip(t−μλ)=0. In caso di scorrimento,

U_tip può essere scelto come moltiplicatore Lagrangiano e (t−μλ) come vincolo per cui

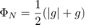
Quando U_tip=0, t=P e t−μλ=62.5>0. Ciò viola la condizione di adesione. Quando U_tip=(P−μλ)L=0.625 mm>0, t=μλ la condizione di scorrimento è soddisfatta (soluzione valida).

2.3 Metodo di penalizzazione

Si penalizza quando t−μλ>0.

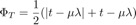
Lo scorrimento (traslazione assiale relativa) viene calcolato come

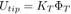
con K_T parametro di penalizzazione per lo scorrimento tangenziale.

Quando t−μ−λ<0 → adesione, U_tip=0 (nessuna penalizzazione). Quando t−μ−λ>0 → scorrimento, si penalizza per rimanere vicino a t=μλ . In caso di scorrimento, la forza di attrito può essere derivata da

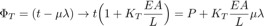
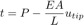
Lo spostamento della punta risultata

Tabella 1: risultati in funzione del parametro di penalizzazione scelto

KT	Spostamento della punta (Utip) [m]	Forza tangenaziale (t) [N]

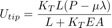
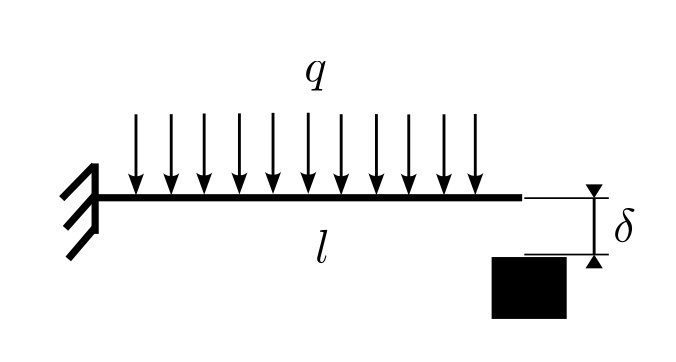
3. Formulazione generale per problemi di contatto

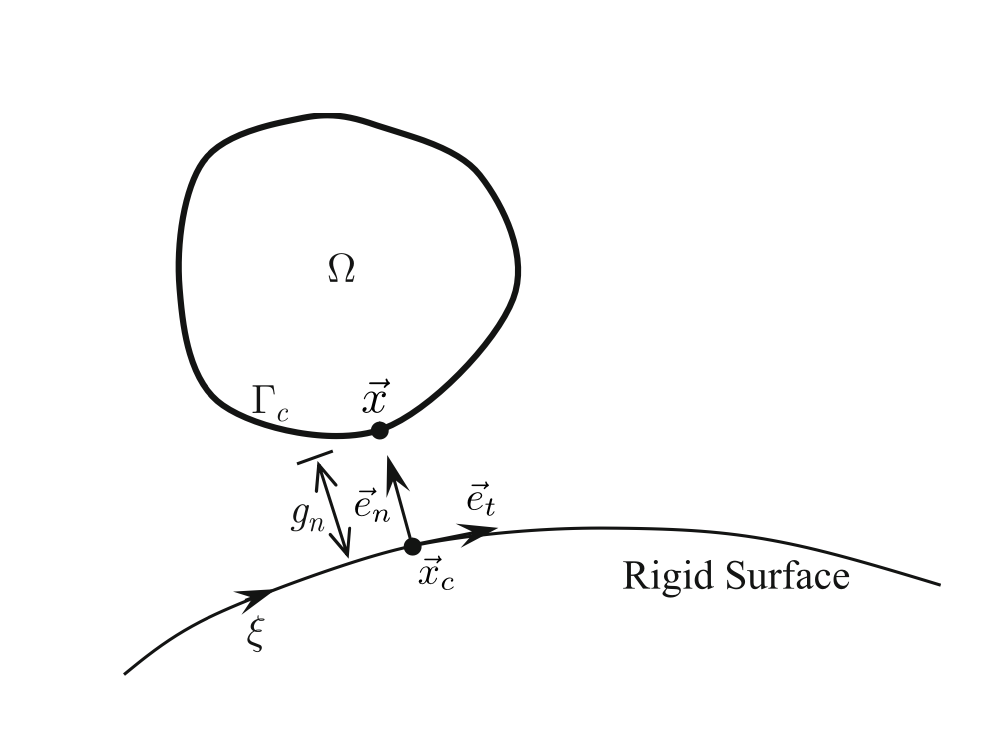
Gli esempi di contatto puntuali descritti nella sezione precedente sono limitati da un punto di vista pratico, poiché la maggior parte dei contatti nelle applicazioni ingegneristiche prevede un contatto distribuito lungo curve o superfici. Nella figura, Γ_C denota la potenziale zona di contatto sul corpo deformabile (slave) che può interagire con una superficie rigida (master) a seguito dell’applicazione di un carico.

L’analisi del contatto diventa significativamente più impegnativa quando si passa da punti discreti a superfici continue. Innanzitutto, l’area di contatto effettiva si evolve durante il carico e deve essere determinata come parte della soluzione. L’utente deve specificare un limite di contatto Γ_C (potenziale area di contatto) sufficientemente grande da comprendere tutte le possibili zone di interazione. Di conseguenza, i problemi di contatto richiedono la determinazione simultanea delle posizioni di contatto precise x_c(ξ_c) sulla superficie master e delle corrispondenti forze di contatto (sia pressioni di contatto che eventuali forze di attrito). Infine, le condizioni di contatto introducono vincoli geometrici non lineari che in genere richiedono strategie di soluzione iterative.

Per ogni punto candidato x ∈ Γ_C, si deve trovare la sua proiezione ortogonale

x_c(ξ_c) sulla superficie master. Ciò si riduce alla risoluzione dell’equazione:

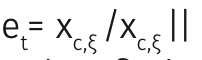
dove il vettore tangente  caratterizza l’origine della superficie locale a ξ_C. La funzione gioco normale:

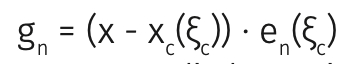
permette di determinare se si verifica un contatto (g_n≤0) o se rimane del gioco (g_n>0). Il versore normale  completa la descrizione della cinematica dei contatti.

Quando il contatto è stabilito, il moto tangenziale relativo viene quantificato attraverso la funzione di scorrimento:

tracciando il movimento lungo la superficie master della configurazione precedente.

ESEMPIO: Superficie di contatto parabolica

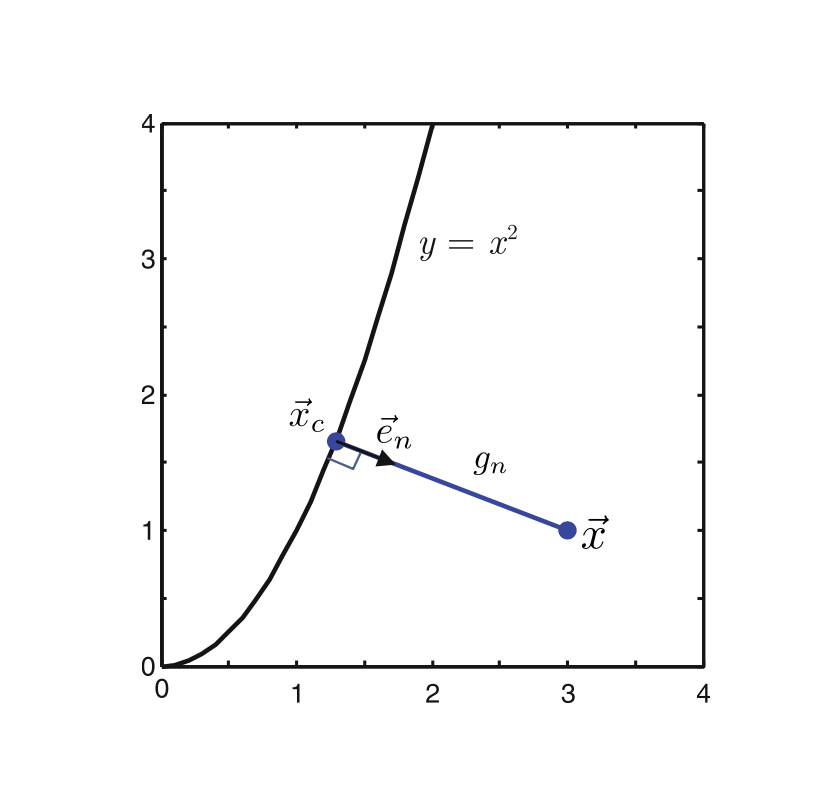
Si consideri la proiezione di un punto x=[3, 1]^T sulla superficie rigida parabolica y=x²

Step di soluzione:

1.         Parametrizzazione della superficie: la superficie master è descritta parametricamente come x_c(ξ)=[ξ,ξ2]^T, con vettore tangente x_c,ξ=[1,2ξ]^T .

2.         Calcolo della proiezione: risoluzione della condizione di coerenza del contatto da cui    l’equazione cubica:

            3+𝜉−2𝜉³=0

            La radice fisicamente significativa ξ_c≈1.29 che individua il punto di contatto in x_c=        [1.29,1.66]^T.

3.         Valutazione del gioco: il calcolo del gioco normale permette di discernere tra     condizione di penetrazione e non, mentre la funzione di scorrimento traccerebbe qualsiasi movimento tangenziale successivo.

Conclusioni

Nelle simulazioni numeriche agli elementi finiti, la risoluzione dei contatti è una delle sfide maggiori. Questa viene affrontata con molteplici approcci. Il più comune è quello della penalizzazione che però richiede una accurata scelta dei parametri per garantire risultati accurati ed un onere computazionale ragionevole.