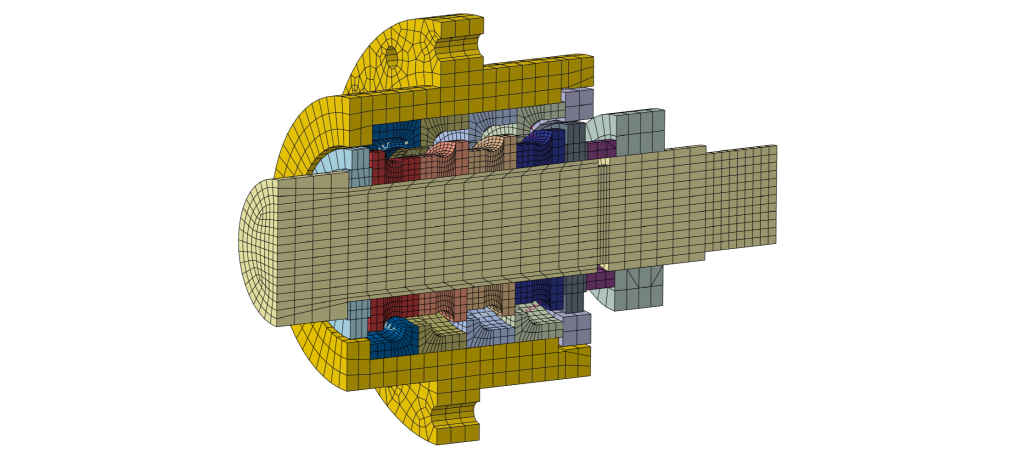
I centri di lavoro sono ampiamente utilizzati nel settore produttivo e la qualità delle lavorazioni meccaniche che essi sono in grado di eseguire è influenzata da diversi fattori, uno dei quali è la vibrazione dell’utensile. Pertanto, diventa di fondamentale importanza conoscere le frequenze di risonanza della macchina e dei suoi componenti, in modo da valutare quanto le frequenze eccitate in esercizio siano lontane da esse. Questo per capire se, già in fase di progettazione, si renda necessario alzare o abbassare le frequenze proprie per evitare o quantomeno ridurre il più possibile vibrazioni indesiderate. In questo articolo si calcolano i modi propri di una vite a ricircolo di sfere.
di Elia Faverzani, Pietro Luigi Frignati, Leonardo Lambertini, Emanuele Maria Scacchi, Cesare Sibra
La vite a ricircolo di sfere e i suoi supporti
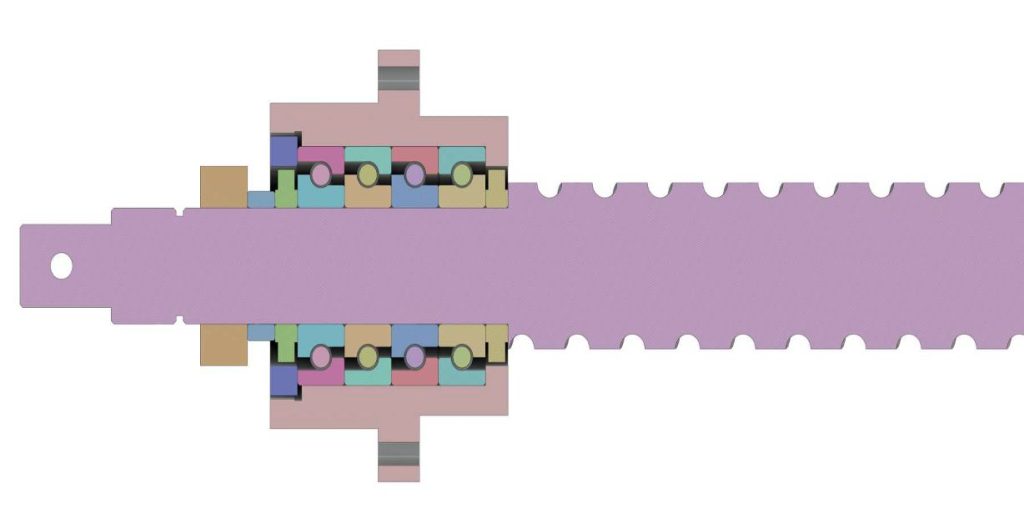
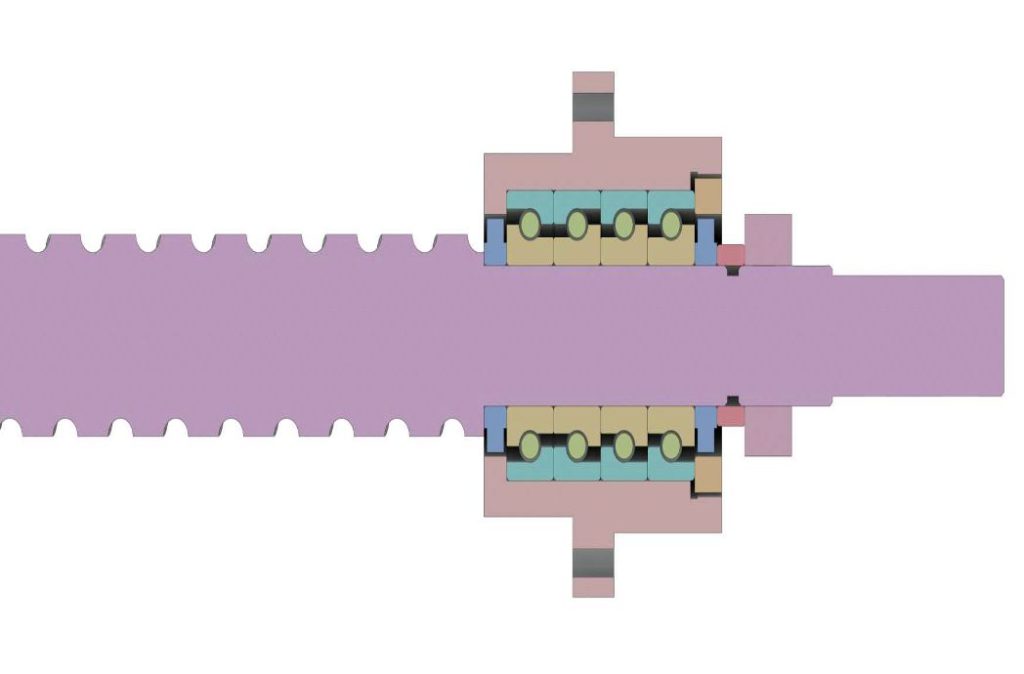

La vite a ricircolo di sfere in questione è supportata alle sue estremità da due gruppi di cuscinetti (Figura 1), posizionati simmetricamente rispetto al centro della vite, costituiti ciascuno da quattro cuscinetti del tipo riportato in Figura 2. La Figura 3 illustra invece il modello CAD di un gruppo di cuscinetti.
Poiché questi gruppi non hanno rigidezza infinita, calcolare le frequenze proprie della vite a ricircolo di sfere vincolando a terra le estremità porterebbe sicuramente a risultati non realistici, con il rischio di ritrovare poi le reali frequenze di risonanza eccitate durante il funzionamento del centro di lavoro. Per questo motivo, è necessario valutare l’effettiva rigidezza dei supporti che sostengono la vite, per poi tenerne conto nell’analisi modale della vite stessa.
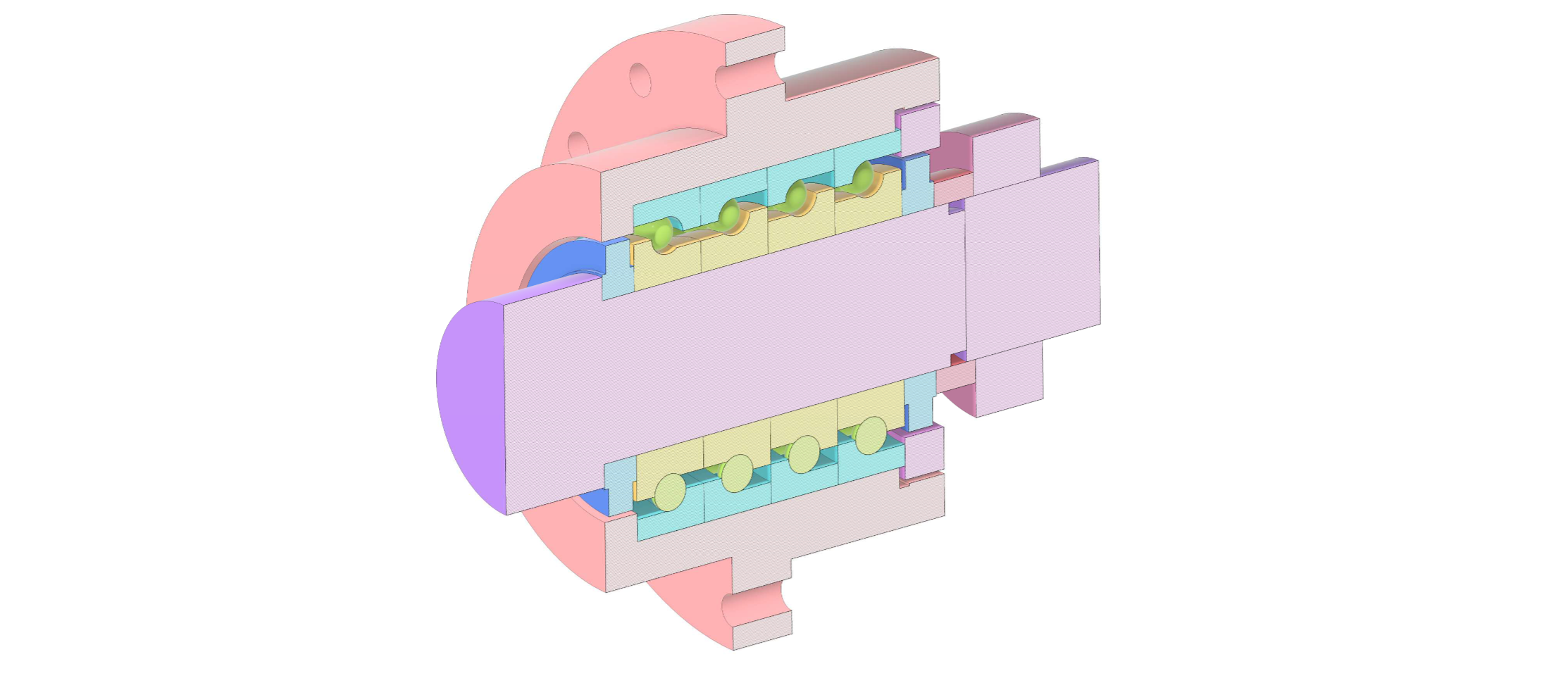
Calcolo della rigidezza del gruppo cuscinetto
Per la valutazione delle rigidezze del gruppo si potrebbe procedere per via sperimentale, ma questo approccio richiederebbe sicuramente tempo e la realizzazione di attrezzature specifiche per poter montare l’assieme da testare su un banco prova.
Conviene quindi procedere con una sperimentazione “virtuale”, ricorrendo al Metodo degli Elementi Finiti e alla sua implementazione in modelli di calcolo che possono essere, ai giorni nostri, molto dettagliati e in grado di fornire risultati estremamente precisi, a fronte di una loro corretta applicazione.
Come si può intuire osservando la Figura 3, il modello da preparare è abbastanza complesso perché deve contenere i quattro cuscinetti a sfere, i componenti necessari a tenerli in posizione e il corpo che li contiene e li fissa al blocco della macchina: tutte queste parti sono in mutuo contatto, comportando un calcolo di tipo non lineare. Inoltre, il valore del precarico da applicare ai cuscinetti ha sicuramente un’influenza sulla rigidezza dell’assieme, ed è pertanto necessario tenerne conto.
Tuttavia, la parte più complessa riguarda la gestione del contatto tra le sfere e le piste nelle quali esse rotolano: chiaramente si può pensare di modellare tutte le 19 sfere per ciascuno dei 4 cuscinetti, ma questo richiederebbe anche la modellazione della gabbia che le contiene, proprio per garantire che esse rispettino la distanza reciproca tra esse, come avviene nella realtà. Questo approccio, inoltre, richiederebbe parecchie risorse, sia umane per la costruzione di mesh adeguate a cogliere i complessi fenomeni che sorgono nel contatto tra le sfere e le piste sia, di conseguenza, computazionali.
Modellazione delle sfere del cuscinetto
Per questo motivo si è deciso di seguire l’approccio descritto in [1] al Capitolo 17, ossia di sostituire le sfere con una molla non lineare, la cui curva viene ricavata sempre con un modello a Elementi Finiti di una singola sfera premuta tra due piani infinitamente rigidi, come illustrato nella Figura 4. Nella medesima figura, viene riportata anche la curva forza/schiacciamento da cui ricavare la rigidezza non lineare da assegnare alle molle.
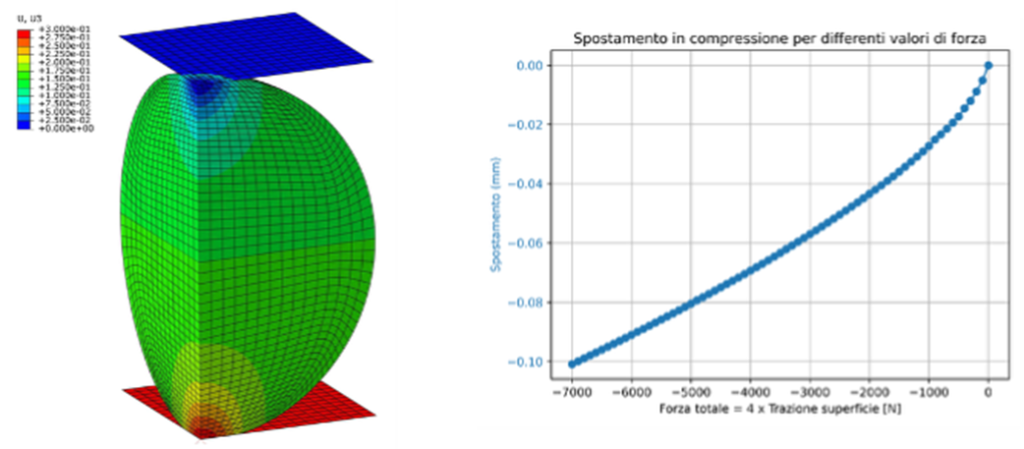
forza/schiacciamento.
Pertanto, il modello a Elementi Finiti del singolo cuscinetto è quello riportato nella Figura 5. L’angolo con cui le molle collegano la pista interna a quella esterna (angolo di pressione) viene ricavato dal catalogo SKF. Si procede poi a collegare le estremità degli elementi molla a elementi di tipo MPC collocati sulle piste: ciò evita le singolarità che si otterrebbero ancorando le estremità degli elementi molla a un singolo nodo sulla pista, che porterebbero all’alterazione dell’effettiva rigidezza del cuscinetto.

Si procede poi alla realizzazione del modello di tutto il gruppo cuscinetti (Figura 6), includendo anche la parte terminale della vite a ricircolo di sfere, che viene utilizzata per introdurre i carichi necessari alla valutazione della rigidezza dell’assieme.
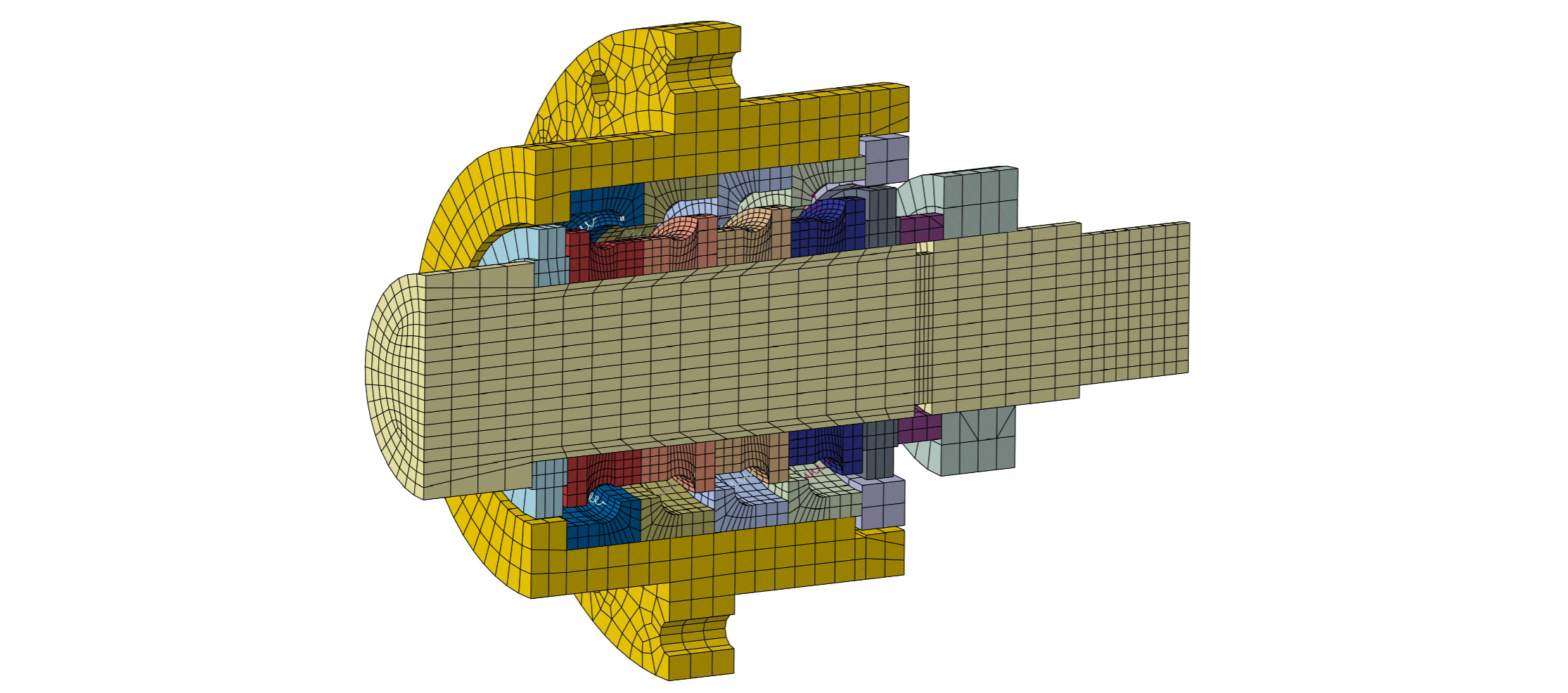
Visto che la rigidezza delle sfere è non lineare (si veda la Figura 4) e considerati i contatti tra le varie parti, ci si aspetta che la rigidezza dell’assieme sia anch’essa non lineare. Innanzitutto, si applica il precarico in termini di spostamento imposto, utilizzando il valore suggerito da SKF per questo gruppo, pari a 0.07 mm.
Come secondo e terzo passaggio, si impone uno spostamento alla porzione di vite inclusa nel modello lungo la direzione assiale della vite, prima in un verso e poi nell’altro, misurando la forza necessaria.
Come quarto e quinto passaggio, si impone una rotazione, sempre alla porzione di vite inclusa nel modello attorno a uno degli assi ortogonali, prima in un verso e poi nell’altro, misurando la coppia necessaria.
Si ottengono infine i grafici riportati nella Figura 7.
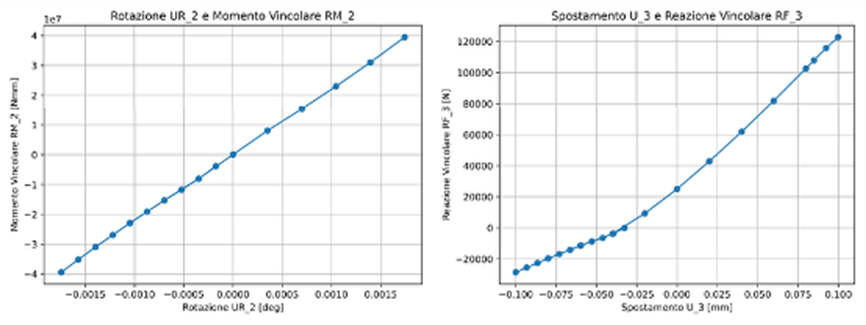
Come si può vedere, per quanto riguarda la rigidezza assiale è presente una discreta non linearità, mentre per quanto riguarda la rigidezza flessionale si ha un andamento pressoché lineare.
Dato che le analisi modali sono per loro natura lineari, è necessario linearizzare queste rigidezze prima di introdurle nel modello della vite; la linearizzazione è ottenuta mediante regressione lineare, ottenendo le rette riportate in Figura 8: i valori dei coefficienti angolari delle rette di regressione rappresentano le rigidezze da attribuire ai vincoli per il modello della vite.
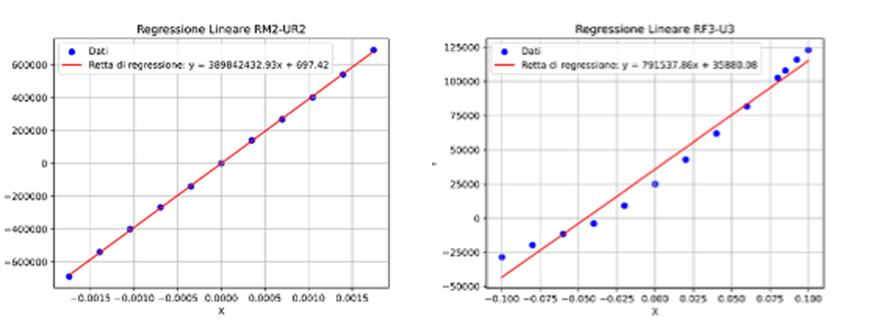
La rigidezza radiale del gruppo cuscinetti non è calcolata: è considerata molto più elevata di quella assiale e di quelle flessionali.
Calcolo della rigidezza del gruppo cuscinetto
A questo punto si può passare alla modellazione della vite: al fine di avere un modello pulito, il tratto filettato è eliminato e sostituito con un cilindro di diametro pari al diametro medio della filettatura, come illustrato in Figura 9.
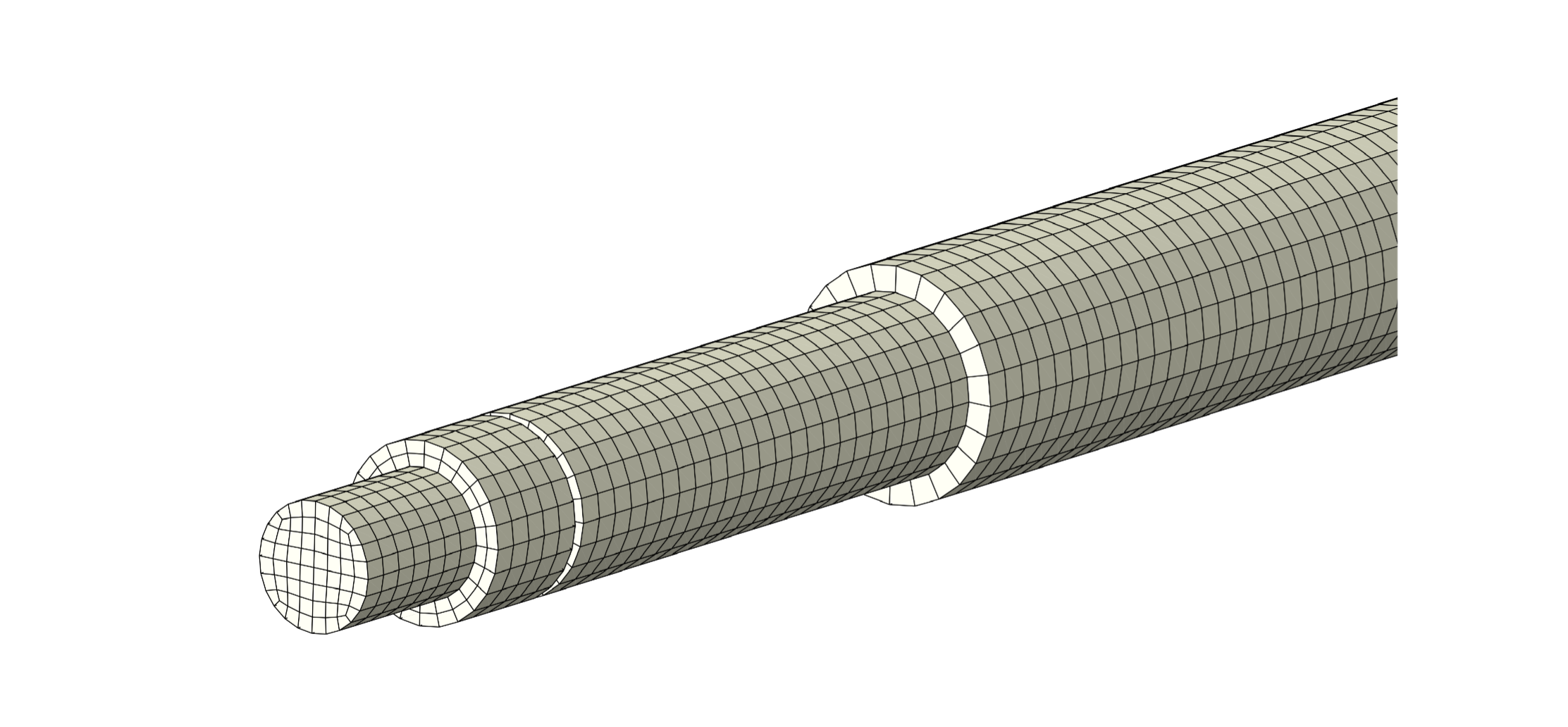
La superficie di contatto della vite con l’anello interno del cuscinetto è collegata al nodo Master di un MPC, cui sono applicate le condizioni di vincolo con elementi molla a terra: la rigidezza di tali elementi è stata assegnata a partire dai risultati ottenuti in precedenza (Figura 10).
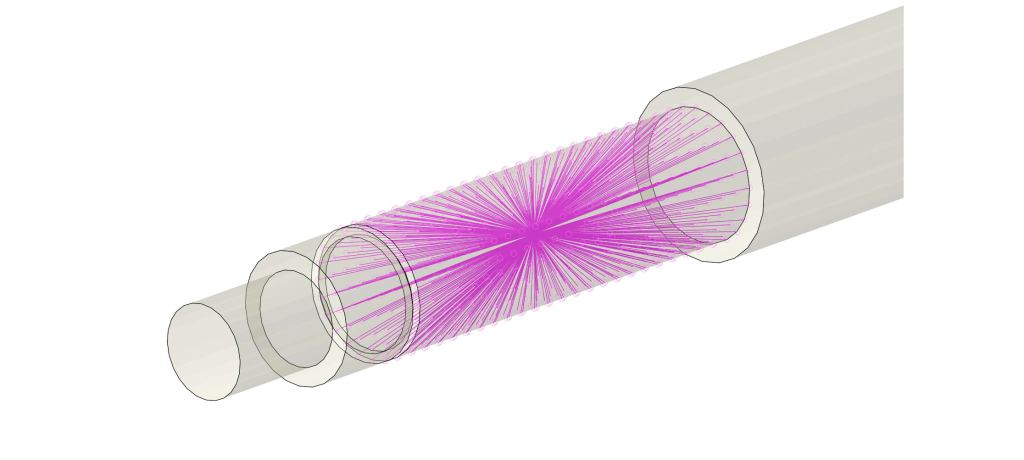
La rotazione assiale e le traslazioni radiali sono vincolate rigidamente: la prima per evitare di avere una rotazione rigida (0 Hz), le altre perché il gruppo cuscinetti è molto rigido radialmente, come accennato in precedenza.
La tabella 1 riporta i valori delle frequenze proprie della vite, vincolata nel modo visto, a confronto con lo stesso modello vincolato rigidamente a terra.
Osservando i risultati si possono fare alcune considerazioni:
- come era prevedibile, le frequenze con i vincoli elastici sono diverse, in particolare sono più basse rispetto al modello a vincoli rigidi, con differenze attorno al 13-15%;
- la frequenza del primo modo torsionale (modo 9) è la stessa nei due casi: questo non deve stupire perché il vincolo sulla rotazione è lo stesso in entrambi i modelli;
- i modi 18 e 19 si invertono: il modo assiale nel caso di vincoli rigidi ha una frequenza molto più alta rispetto al modello con vincoli elastici.
| MODE NUMBER | FREQUENCY | TYPE | MODE NUMBER | FREQUENCY | TYPE |
| 1 | 21.98 | Bending | 1 | 25.15 | Bending |
| 2 | 21.98 | Bending | 2 | 25.15 | Bending |
| 3 | 60.78 | Bending | 3 | 69.25 | Bending |
| 4 | 60.78 | Bending | 4 | 69.25 | Bending |
| 5 | 119.43 | Bending | 5 | 135.53 | Bending |
| 6 | 119.43 | Bending | 6 | 135.53 | Bending |
| 7 | 197.64 | Bending | 7 | 223.54 | Bending |
| 8 | 197.64 | Bending | 8 | 223.54 | Bending |
| 9 | 273.43 | Torsional | 9 | 273.43 | Torsional |
| 10 | 295.23 | Bending | 10 | 333.01 | Bending |
| 11 | 295.23 | Bending | 11 | 333.01 | Bending |
| 12 | 411.81 | Bending | 12 | 463.57 | Bending |
| 13 | 411.81 | Bending | 13 | 463.57 | Bending |
| 14 | 546.81 | Bending | 14 | 614.81 | Bending |
| 15 | 546.81 | Bending | 15 | 614.81 | Bending |
| 16 | 699.41 | Bending | 16 | 786.28 | Bending |
| 17 | 699.41 | Bending | 17 | 786.28 | Bending |
| 18 | 704.13 | Axial | 18 | 820.31 | Torsional |
| 19 | 820.31 | Torsional | 19 | 907.64 | Axial |
| 20 | 868.41 | Bending | 20 | 977.45 | Bending |
Conclusioni
Trascurare l’effettiva rigidezza del sistema di vincolo della vite a ricircolo di sfere avrebbe portato a un’errata valutazione delle sue frequenze proprie, con il rischio di ritrovare poi nella macchina completa delle vibrazioni che avrebbero potuto pregiudicare la qualità delle lavorazioni eseguite con essa.
L’ottenimento di valori di rigidezza attendibili da usare come condizioni al contorno è stato possibile grazie alla realizzazione di un dettagliato modello a Elementi Finiti, certamente articolato ma semplificato e alleggerito grazie all’adozione di un sistema che ha consentito di evitare la modellazione di tutte le sfere, con conseguente risparmio di tempo e di risorse umane e di calcolo.