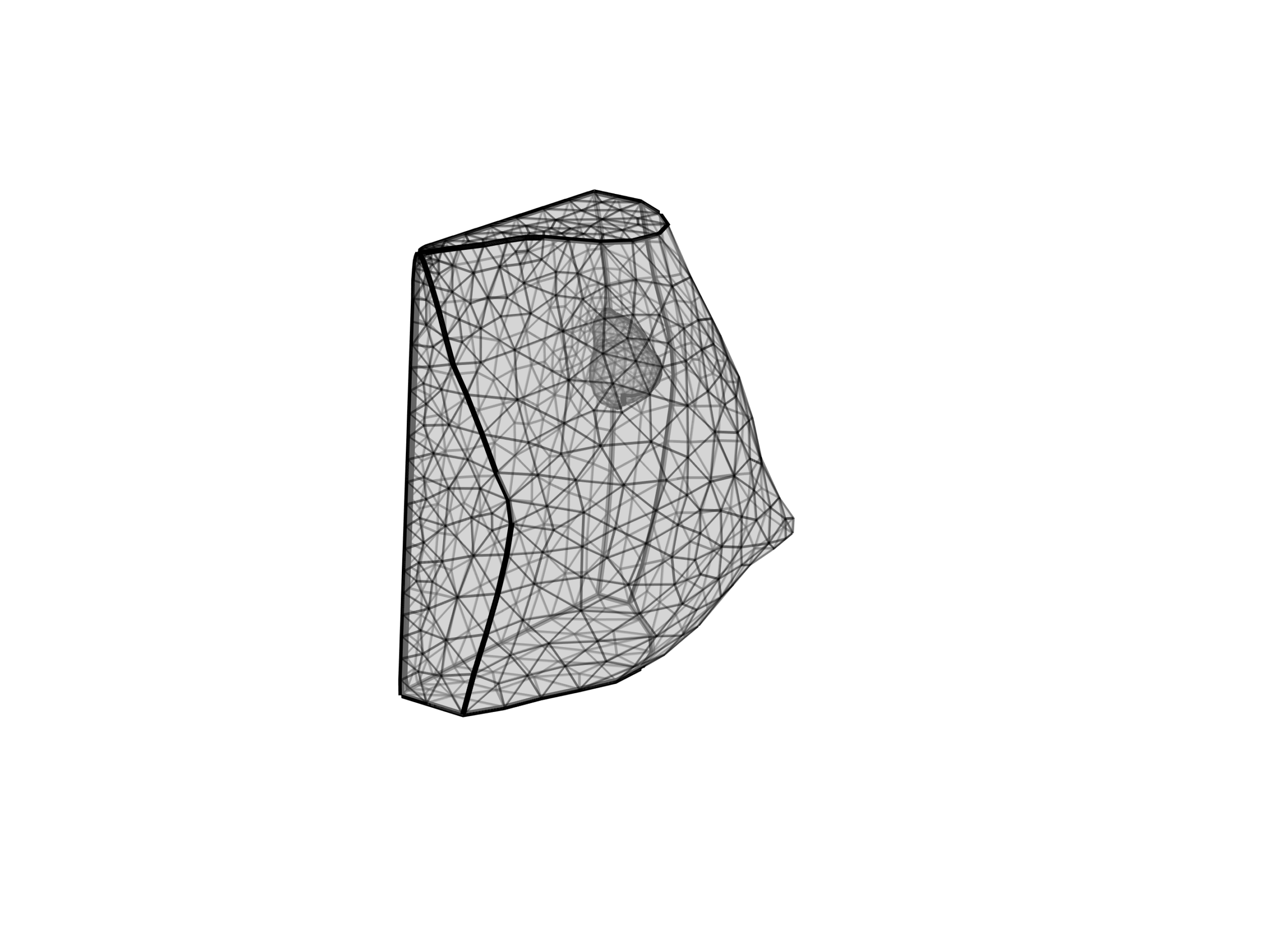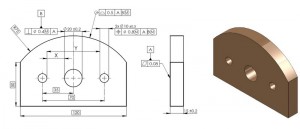
Fig. 1. – Calcolo della distanza X e Y tra i bordi dei fori; poiché il riferimento B è una feature con tolleranza dimensionale, su questo è stato applicato un modificatore di massimo materiale che consente un ulteriore aumento della zona di errore (shift).
Il calcolo di distanze e interassi in presenza di tolleranze geometriche di localizzazione è estremamente complicato, soprattutto se durante il collaudo è necessario tener conto di tolleranze addizionali dovute al modificatore di massimo materiale per la tolleranza (Bonus) o addirittura sul riferimento (Shift)
Le distanze funzionali tra i fori possono essere calcolati con la catena tradizionale, seguendo la metodologia esposta nel quaderno di progettazione di giugno 2011 e riportata in figura 2.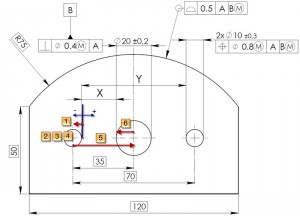
La procedura risulta particolarmente complicata poiché ad esempio è necessario calcolare lo shift minimo nella colonna della tabella in cui l’elemento di riferimento è al massimo materiale e lo shift massimo nella colonna in cui l’elemento di riferimento è al minimo materiale. Per questo motivo viene illustrata una nuova procedura semplice e immediata attraverso delle considerazioni sulle dimensioni del contorno del foro, definendo una relazione dinamica e funzionale tra la dimensione del foro soggetta a tolleranza dimensionale e la tolleranza di posizione. Supponiamo di eseguire il calcolo nella condizione di massimo materiale che, nel caso del foro da 10 mm di figura 3, corrisponde a 9,7 mm. Se si considerano tutte le posizioni assunte dal foro all’interno della zona di tolleranza di 0.8 mm, viene ottenuto un contorno interno da non violare che definisce la dimensione virtuale cioè il contorno teorico interno di accoppiamento (Inner Boundary, IB); la dimensione virtuale è una quantità costante (8,9 mm), ottenuta sottraendo la tolleranza al massimo materiale (0.8) dalla dimensione di massimo materiale (9,7).
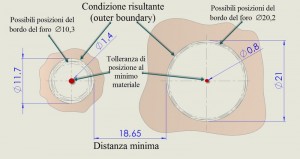
Allo stesso modo, nelle condizioni di minimo materiale del foro (10.3, fig. 4), se si considerano tutte le posizioni assunte dal foro all’interno della zona di tolleranza di 1,4 mm, è possibile definire la condizione risultante (11,7, contorno teorico esterno, Outer Boundary, OB). La condizione risultante si ottiene addizionando la tolleranza al minimo materiale (1,4) alla dimensione di minimo materiale (10,3). Si tenga presente che per gli alberi si dovrà procedere ad un calcolo diverso.
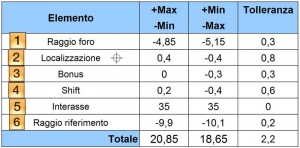
Volendo ottenere le dimensioni dei contorni dei fori della figura 1, si otterrà:
Per il foro da 10 mm: IB1= 9,7-0,8 = 8,9 OB1= 10,3+1,4= 11,7
Per il foro da 20 mm: IB2= 19,8-0,4 = 19,4 OB2= 20,2+0,8 = 21
La distanza X sarà ottenuta sottraendo dall’interasse teorico i due contorni limiti teorici (in termini radiali) e quindi sarà uguale a:
Xmax = 35- (IB1 + IB2 )/2 = 35-14.5 = 20.85 (figura 3)
Xmin = 35- (OB1 + OB2 )/2 = 35-16.35 = 18.65 (figura 4)
Lasciamo al lettore il calcolo della distanza Y massima e minima (uguale a 61,1 e 58,3).
