Analizziamo i criteri per la progettazione statica e dinamica degli alberi di trasmissisone e alcuni accorgimenti costruttivi
di Giorgio De Pasquale1, Elena Perotti2, Giorgio Avanzato1
1 Smart Structures and Systems Lab, Dip. di Ingegneria Meccanica e Aerospaziale, Politecnico di Torino.
2 Senior data analyst.
Introduzione
Come noto, il termine “albero di trasmissione” comunemente denota un elemento strutturale cilindrico in grado di ruotare e trasmettere potenza da una fonte motrice, come ad esempio un motore o un’altra unità, all’interno di una macchina. La funzione principale degli alberi di trasmissione è quella di trasferire il moto rotatorio e la potenza attraverso meccanismi come ruote dentate, pulegge e catene o altri. In alternativa, un albero di trasmissione può essere progettato per connettersi a un altro albero mediante l’impiego di accoppiamenti specifici. In applicazioni differenti, è possibile trovare anche alberi di trasmissione che rimangono in condizioni stazionarie mentre supportano un elemento rotante: è il caso ad esempio di alberi di ridotta lunghezza utilizzati per supportare ruote non motrici di veicoli [1].
La progettazione degli alberi di trasmissione richiede di considerare alcuni aspetti fondamentali, tra cui possiamo citare: (a) il dimensionamento, il posizionamento e il montaggio dei componenti nell’assieme complessivo considerando le rispettive tolleranze di lavorazione, (b) la scelta dei materiali e i loro trattamenti, (c) la rigidezza e la inflessione sotto carico (legate al concetto di linea elastica, momento flettente, momento torcente, accoppiamento taglio-flessione, inclinazione ai cuscinetti), (c) le sollecitazioni interne (resistenza statica, fatica, affidabilità), (d) il comportamento dinamico, (e) i vincoli di fabbricazione [1].
2. Varianti costruttive e di progetto
2.1. Geometria
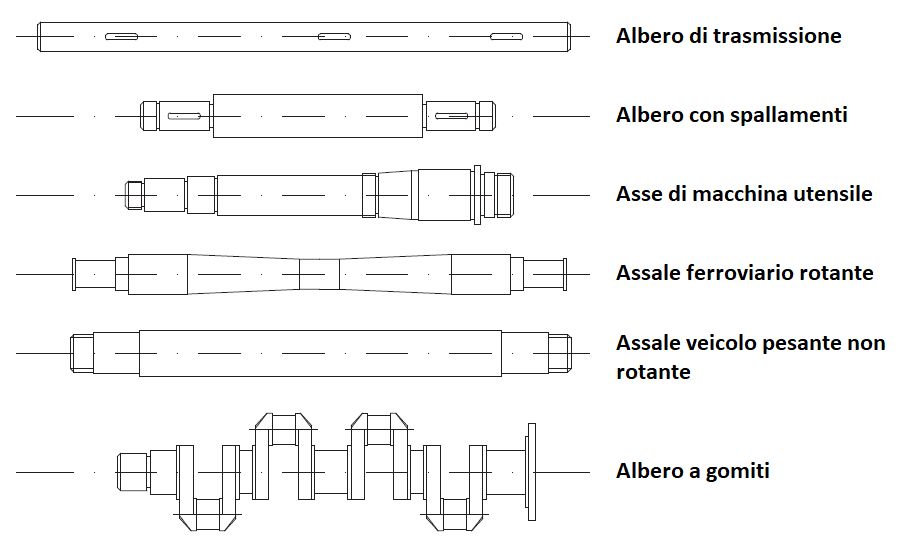
Gli alberi di trasmissione sono ovviamente elementi centrali nella progettazione di sistemi meccanici e di conseguenza possono presentare configurazioni molto complesse nella loro forma, con sequenze di spallamenti, variazioni di diametro e sezione, spostamento del baricentro, e altro. Questi dettagli costruttivi servono molto spesso a fornire un riferimento geometrico per il montaggio e un riscontro fisico per supportare carichi assiali, come nel caso del montaggio di cuscinetti. Spesso però la geometria dell’albero serve a ospitare elementi costruttivi con funzioni più specifiche, come elementi per il montaggio di ruote dentate (si impiegano chiavette o linguette per prevenire movimenti relativi indesiderati), di guarnizioni o tenute per il lubrificante, di elementi scanalati, di elementi filettati, etc. In Figura 1 si riportano alcuni esempi dei più comuni alberi di trasmissione.
La progettazione dell’albero deve garantire che la sua deformata flessionale (in primo luogo) sia mantenuta entro livelli accettabili. Flessioni eccessive potrebbero impattare negativamente sulle prestazioni degli ingranaggi, generando disturbi acustici e vibrazioni indesiderate. Il valore massimo consentito per la flessione di un albero è generalmente determinato da vincoli legati alla velocità critica, ai disallineamenti massimi tollerati dalle ruote dentate per il loro corretto ingranamento e i requisiti specifici dei cuscinetti. In generale, si raccomanda che la flessione dell’albero non causi una separazione fra i denti degli ingranaggi superiore a 0.13 mm e un disallineamento fra i loro assi superiore a 0.03° [1].
Per quanto riguarda la eccessiva rotazione della sezione dell’albero, conseguente a deformazione flessionale, in corrispondenza dei cuscinetti, è anch’essa fonte di potenziali problemi. In questi casi, il disallineamento non dovrebbe mai superare lo spessore del film d’olio presente tra i corpi volventi del cuscinetto. In generale, sempre come dato di riferimento, è bene che il disallineamento della sezione in corrispondenza dei cuscinetti non superi i 0.04 gradi. Per prevenire problemi di questo tipo è piuttosto consigliabile ricorrere a cuscinetti orientabili, in grado di lavorare entro un range di inclinazione angolare fra anello interno ed esterno.
Gli alberi, nell’ambito delle trasmissioni meccaniche, vengono sottoposti a una combinazione di carichi assiali, flessionali e torsionali. Tali carichi possono variare nel tempo e generare complesse condizioni dinamiche. In particolare, un albero in rotazione adibito alla trasmissione di potenza è solitamente soggetto a una coppia torcente costante abbinata a una sollecitazione flessionale che produce invece tensioni alterne variabili nel tempo. Si genera quindi una sollecitazione torsionale costante e una flessionale alternata.
Nel corso della progettazione dell’albero, è importante ricordare questi principi di base:
- Ottimizzare la lunghezza degli alberi, mantenendoli il più corti possibile, con i cuscinetti posizionati in prossimità dei carichi applicati. Questa strategia mira a ridurre la deformata flessionale dell’albero, i momenti flettenti e a incrementare le velocità critiche.
- Quando possibile, collocare gli spallamenti e altre fonti di intensificazione delle tensioni lontano dalle zone dell’albero più sollecitate. Utilizzare raggi di raccordo più ampi possibile in presenza di intagli, finiture superficiali lisce e processi di rinforzo superficiale del materiale.
- In situazioni in cui il peso proprio dell’albero diventa rilevante, sia in termini statici sia dinamici, considerare l’utilizzo di alberi cavi per ottimizzare le prestazioni.
2.2. Velocità critiche di funzionamento
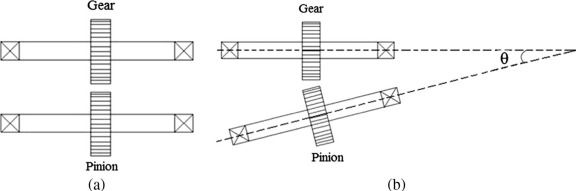
La progettazione degli alberi deve evitare se possibile il funzionamento alla velocità critica o in prossimità di essa. Tale obiettivo si può solitamente ottenere mediante una adeguata rigidezza flessionale, affinché la velocità critica più bassa sia sensibilmente superiore all’intervallo di velocità operative. Nel caso di fluttuazioni di coppia motrice, ovvero di sollecitazioni torsionali, tipiche degli alberi motore, le frequenze naturali di tipo torsionale dell’albero devono essere il più possibile distanti dalla frequenza torsionale in ingresso. In questo caso, il requisito progettuale può essere ottenuto incrementando la rigidezza torsionale dell’albero e garantendo che la frequenza naturale più bassa dell’albero sia notevolmente superiore alla frequenza torsionale di ingresso più alta.
2.3. Montaggio dei cuscinetti
Gli alberi in rotazione richiedono solitamente di essere supportati tramite cuscinetti per garantirne il posizionamento, la stabilità e la corretta funzionalità. Nella maggioranza dei casi è consigliabile utilizzare cuscinetti di supporto in due soli punti dell’albero, impiegando quindi solamente due set di cuscinetti. Se, in casi molto particolari, fosse necessario supportare l’albero in più di due punti, diviene estremamente importante fornire un preciso allineamento di tutti i cuscinetti e garantire che tale allineamento permanga durante l’esercizio. L’assorbimento dei carichi assiali e il corretto posizionamento assiale dell’albero sono tipicamente gestiti attraverso l’applicazione di un singolo cuscinetto assiale (detto “reggispinta”). Una coppia di cuscinetti reggispinta non è idonea in tutti i casi in cui l’albero può andare incontro a dilatazioni termiche per variazione di temperatura in esercizio. È di fondamentale importanza che gli elementi strutturali responsabili del supporto dei cuscinetti siano caratterizzati da una sufficiente resistenza e rigidezza.
3. Collegamenti albero-mozzo
Tutti i componenti necessari per la trasmissione di potenza, come ingranaggi, pulegge e catene, richiedono un montaggio sicuro sugli alberi e un preciso posizionamento assiale rispetto agli altri componenti ad essi accoppiati. Allo stesso tempo, è essenziale garantire una sicura trasmissione della coppia, ovvero senza scorrimenti relativi indesiderati e senza sovraccarichi locali delle superfici a contatto, tra l’albero e il componente. Il componente a diretto contatto con l’albero è denominata “mozzo” e può essere realizzata in modo solidale all’albero stesso (“di pezzo”), oppure vincolata all’albero mediante chiavette, linguette, perni, viti senza testa, accoppiamento a pressione e a caldo, nonché tramite scanalature e boccole coniche. In alternativa ai metodi di accoppiamento descritti è possibile realizzare in componente in modo integrato sull’albero, come nel caso delle camme di un albero di distribuzione (Figura 3).
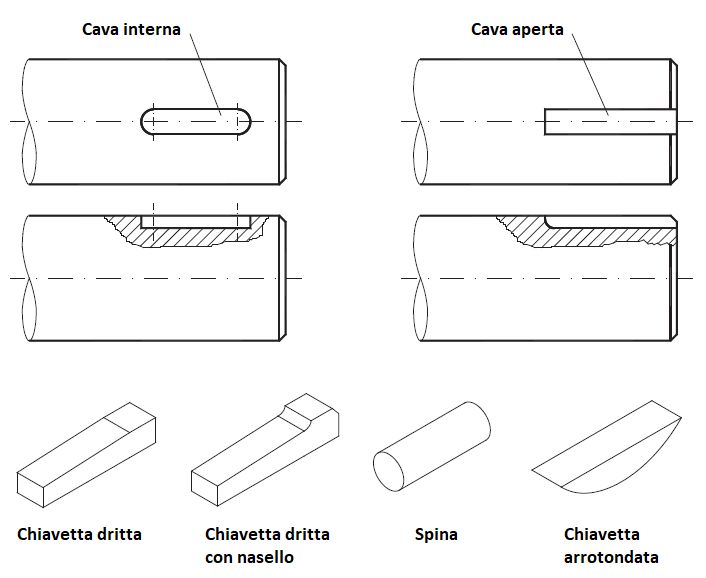
Per l’accoppiamento di ruote dentate, una soluzione efficace si ottiene prevedendo uno spallamento sull’albero e un distanziale dal lato opposto, utilizzando una chiavetta o linguetta per la trasmissione della coppia. Esistono diverse configurazioni per le chiavette, tra cui ad esempio le chiavette quadrate, quelle piatte e quelle tonde, come evidenziato in Figura 4. Le sedi opportune devono essere realizzate con le dimensioni e le tolleranze previste da normativa su albero e mozzo (UNI 6604, DIN 6885).
Per trasmettere carichi leggeri in modo più semplice ed economico, è possibile impiegare spine e varie tipologie di perni. Un approccio pratico ed economico per garantire la corretta posizione assiale di mozzi e cuscinetti sugli alberi è l’utilizzo degli anelli elastici.
Un esempio di connessione albero-mozzo che si distingue per la sua semplicità è rappresentato dall’accoppiamento per interferenza, nel quale il foro del mozzo ha un diametro leggermente inferiore al diametro dell’albero. L’assemblaggio può essere ottenuto mediante pressatura o mediante espansione termica del mozzo a seguito di riscaldamento in forno e successiva contrazione termica mediante l’utilizzo di azoto liquido.
Gli accoppiamenti scanalali, invece, si basano su dentature parallele all’asse dell’albero e del mozzo realizzate su entrambi i componenti che entrano in presa in modo da distribuire il carico in modo molto efficace. Essi rappresentano uno dei metodi più robusti per la trasmissione della coppia. Sia le scanalature che le chiavette possono essere progettate per consentire lo scorrimento assiale lungo l’albero, garantendo ulteriore versatilità dell’applicazione.

4. Accoppiamenti tra alberi
Per trasferire coppia e rotazione in modo efficiente da un albero all’altro è possibile utilizzare diversi tipi di accoppiamento rigido, flessibile o a frizione. Gli accoppiamenti rigidi sono progettati per stabilire una connessione tra due alberi tale da evitare qualsiasi movimento relativo tra di essi (Figura 5). Questa tipologia si dimostra particolarmente idonea quando è essenziale mantenere un preciso allineamento tra due alberi. Tuttavia, in presenza di significativi disallineamenti radiali o assiali, potrebbero generarsi sollecitazioni elevate, con conseguente rischio di cedimenti localizzati.
Gli accoppiamenti flessibili sono concepiti per trasmettere la coppia consentendo contemporaneamente un certo grado di disallineamento assiale, radiale e angolare. In commercio esistono diverse configurazioni di accoppiamenti flessibili, consultabili nei cataloghi dei produttori. Ciascun accoppiamento è progettato per trasmettere una specifica coppia limite. In generale, gli accoppiamenti flessibili sono in grado di tollerare disallineamenti angolari fino a 3 gradi e disallineamenti assiali fino a 0.75 mm, a seconda della loro progettazione [1]. In situazioni in cui è necessario gestire disallineamenti più significativi, può essere impiegato un giunto cardanico. Le frizioni sono sistemi più complessi, composti da elementi elastici come molle a tazza o ad elica, ed elementi di attrito. Quando la frizione è innestata, gli elementi di attrito sono sottoposti al carico dei corpi elastici e trasmettono la coppia attraverso la frizione stessa. Al contrario, quando viene disinnestata, ingresso e uscita diventano indipendenti e svincolati e i due alberi collegati non sono più in comunicazione.

5. Velocità critiche e deformata dinamica
5.1. L’equilibrio dinamico
Un corpo in rotazione, come ad esempio un disco calettato su un albero supportato da cuscinetti alle estremità, presenta un centro di massa che non coincide con il centro geometrico nominale del sistema. Questo avviene a causa soprattutto di disallineamenti di montaggio e di tolleranze costruttive legate ai processi di fabbricazione. Inoltre, la forza centrifuga che interessa il corpo in rotazione induce una spinta verso l’esterno proporzionale alla massa coinvolta e genera di conseguenza una curvatura flessionale dell’albero. L’entità di questa curvatura è direttamente proporzionale all’eccentricità costruttiva del sistema e alla forza centrifuga risultante. Si definiscono per ogni sistema alcune velocità critiche di rotazione; in particolare, al di sotto della più bassa velocità critica, la forza centrifuga è efficacemente bilanciata dalla forza elastica legata alla rigidezza dell’albero e si determina un equilibrio che definisce una determinata inflessione dell’albero.
L’entità di questa inflessione viene mantenuta a livelli contenuti dagli effetti dissipativi interni ed esterni al sistema rotante. Fenomeni come la dissipazione energetica nei cuscinetti (in cui avvengono fenomeni di attrito viscoelastico fra i corpi volventi), l’isteresi interna al materiale soggetto a deformazione, altre perdite per attrito che determinano producono un effetto smorzante che limita l’entità della inflessione dinamica dell’albero. Al raggiungimento della velocità critica di rotazione, invece tale inflessione può raggiungere livelli elevati, tali da causare la rottura dell’albero, danneggiare i cuscinetti e generare vibrazioni distruttive nell’intera macchina. Pertanto, è fondamentale determinare accuratamente le velocità critiche di funzionamento, le relative deformazioni flessionali dell’albero e valutarne attentamente le possibili conseguenze. Strumenti come il “diagramma di Campbell” sono utilizzati per analisi di questo tipo.
La velocità critica di rotazione può essere stimata a partire dalla frequenza propria flessionale dell’albero. Questa frequenza si può misurare “colpendo” l’albero fermo con un martello e monitorando la frequenza di vibrazione risultante. Per tutti gli alberi, ad eccezione di quelli con massa concentrata singola, le velocità critiche si manifestano anche a frequenze più elevate. Questo fenomeno sottolinea l’importanza di una progettazione attenta e di una valutazione dettagliata delle dinamiche strutturali per garantire il corretto funzionamento degli alberi in vari contesti applicativi.
5.2. Velocità critiche e velocità operative
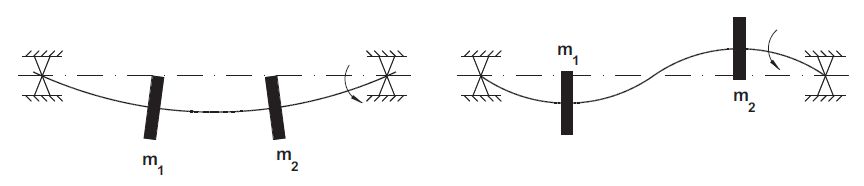
Alla prima velocità critica, l’albero si deforma secondo il modo più elementare possibile, corrispondente alla prima deformata flessionale. Alla seconda velocità critica assumerà una configurazione elementare successiva. Ad esempio, le modalità di deformazione dell’albero alle prime due velocità critiche (o modi di vibrare) per un albero supportato alle estremità con due masse sono illustrate nella Figura 7.
In determinate circostanze, potrebbe essere complicato progettare l’albero in modo da innalzare la prima frequenza naturale del sistema al di sopra della frequenza di lavoro. In questi casi, sempre che il controllo della macchina in questione lo consenta, si può procedere ad accelerare la rotazione rapidamente per superare la velocità critica, senza lasciare il tempo che le vibrazioni indotte dalla risonanza possano accumulare ampiezze significative. In questo modo, il sistema ha la possibilità di “attraversare” la velocità critica e di continuare a operare al di sopra di essa. Lo stesso accorgimento dovrà essere adottato anche nella fase di riduzione della velocità ed occorre prestare attenzione a non incontrare velocità critiche superiori alla prima per evitare problemi analoghi di risonanza. Questo scenario è particolarmente rilevante nelle turbine a vapore e a gas, dove le dimensioni considerevoli delle turbomacchine e dei generatori impongono una bassa frequenza naturale, ma ci si trova nella necessità di farle operare ad alte velocità per ragioni di efficienza.
L’esecuzione di una completa analisi delle frequenze naturali di un albero può essere condotta mediante l’utilizzo di software di simulazione agli elementi finiti, per mezzo di “analisi modali”. Tale approccio fornisce un’ampia gamma di frequenze naturali in tre dimensioni, partendo dalla frequenza fondamentale. Sebbene questo è senz’altro un approccio sensato per sistemi complessi, è opportuno sottolineare può essere condotta una stima più rapida per sistemi semplici allo scopo di facilitare il processo di progettazione. Vediamo qualche considerazione utile in tal senso.
La velocità critica di un albero con una sola massa collegata può essere approssimata come:
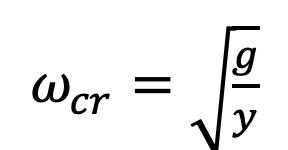
in cui wcr è la velocità critica (rad/s), g è l’accelerazione di gravità (m/s2) e y è la freccia (o inflessione) in corrispondenza della massa concentrata (m).
La determinazione della prima velocità critica di un albero che sostiene varie masse concentrate può essere approssimata attraverso l’utilizzo dell’equazione di Rayleigh-Ritz, come descritto nell’equazione (2). Le inflessioni dinamiche di un albero sono solitamente una grandezza incognita. La metodologia di Rayleigh si basa su una stima della linea elastica (ovvero della curva di inflessione) che rispetta le condizioni al contorno specifiche, ovvero i vincoli presenti sull’albero. Il metodo si basa sulla curva di flessione statica, derivante dal peso proprio dell’albero e dal peso dei componenti collegati. In questa analisi vengono esclusivamente considerati i carichi interni generati dalla forza di gravità, senza tener conto dei carichi esterni.
Il risultato di questo calcolo fornisce un valore leggermente superiore rispetto alla frequenza naturale effettiva dell’albero, con una deviazione percentuale che può variare. Tale approccio offre una base solida per la valutazione preliminare della prima velocità critica di un sistema albero-masse, pur mantenendo una consapevolezza della sua limitata precisione. Inoltre, l’assenza di carichi esterni si riferisce ad una condizione ideale che, nella pratica, può essere affrontata con tecniche di correzione e di adattamento per migliorare la precisione del risultato finale.
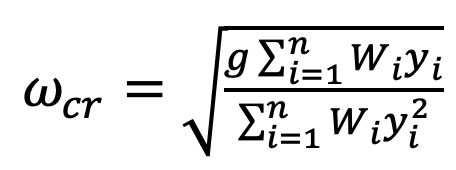
in cui wcr è la velocità critica (rad/s), g è l’accelerazione di gravità (m/s2), y è la freccia (o inflessione) in corrispondenza della massa Wi (m).
Una alternativa all’equazione di Rayleigh-Ritz per la stima della velocità critica è l’equazione di Dunkerley:
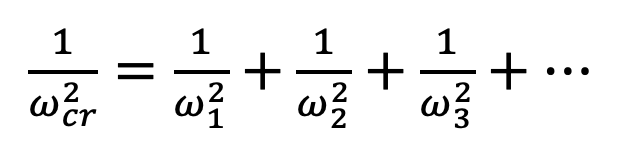
in cui w1 è la velocità critica del sistema nel caso in cui fosse presente solo la massa 1, e così via.
Sia l’equazione di Rayleigh-Ritz sia l’equazione di Dunkerley sono approssimazioni della prima frequenza naturale di vibrazione dell’albero con masse calettate su di esso (rappresentati per esempio ruote dentate, pulegge, dischi, etc.), che si assume essere quasi uguale alla velocità critica. L’equazione di Dunkerley tende a sottostimare il valore della velocità critica, mentre l’equazione di Rayleigh-Ritz tende a sovrastimarne il valore. Pertanto, un valido approccio potrebbe essere quello di calcolare entrambi i valori e metterli a confronto: la reale velocità critica sarà compresa fra le due.
6. Scelta del materiale
La scelta del materiale per una componente costruttivo della macchina rappresenta una delle decisioni più critiche per il progettista. Gli alberi di trasmissione sono comunemente realizzati mediante lavorazione di barre in acciaio al carbonio semplice (AISI/SAE 1020-1050) o acciaio legato (AISI/SAE 4140, 4145, 4150, 4340 e 8620), nelle varianti trafilato a freddo o laminato a caldo.
Tipicamente, gli acciai trafilati a freddo sono utilizzati per alberi di dimensioni ridotte, inferiori a 70 mm, mentre gli acciai laminati a caldo sono comunemente utilizzati per dimensioni maggiori. Il processo di trafilatura a freddo non solo migliora la resistenza meccanica, ma anche la lavorabilità, la finitura superficiale e l’accuratezza dimensionale. Gli alberi in acciaio laminati a caldo sono spesso temprati e rinvenuti per ottenere una maggiore resistenza e successivamente rifiniti (torniti o rettificati e lucidati) per migliorare la finitura e l’accuratezza dimensionale. Quando è richiesta una resistenza superiore, come nel caso di macchinari ad alta velocità, si utilizzano acciai legati come nichel, nichel-cromo o acciai al cromo vanadio. Quando è richiesta anche una buona resistenza alla corrosione, si ricorre a leghe di rame.
7. Fattore di sicurezza
Il coefficiente (o fattore) di sicurezza (CdS) è un termine che descrive la capacità di carico di un sistema, indipendentemente dai valori attesi o effettivi delle sollecitazioni. Di fondamentalmente importanza, esso identifica quantitativamente la sovra-resistenza di un sistema rispetto alle sue condizioni nominali di lavoro previste. In ambito progettuale, si opera dimensionando i componenti in modo che siano più resistenti rispetto a quanto richiesto sarebbe necessario per un utilizzo normale, al fine di sopportare anche situazioni di emergenza, carichi inaspettati, usi impropri o degrado.
La scelta del CdS per una particolare applicazione è una delle attività ingegneristiche più importanti. Il problema consiste nel valutare le molte incertezze associate ai modelli che si utilizzano nella progettazione, a quelle legate alle proprietà dei materiali e al livello di danno associato a un potenziale cedimento. La valutazione finale deve essere espressa considerando elementi quali, appunto, sicurezza, normativa di riferimento, peso, presenza di ridondanze, etc.
Elementi determinanti per la valutazione del CdS sono il grado di conoscenza dei carichi effettivi, dell’ambiente operativo, delle proprietà di resistenza dei materiali, delle approssimazioni del metodo di calcolo. I valori del CdS tipicamente variano da 1.3 a 6, a seconda degli elementi elencati o dalle imposizioni delle normative del settore di riferimento. A meno di circostanze speciali, valori di CdS inferiori a 1.5 non sono consigliati. Di contro, valori troppo elevati potrebbero compromettere il funzionamento del sistema (si pensi ad esempio al peso di un velivolo).





