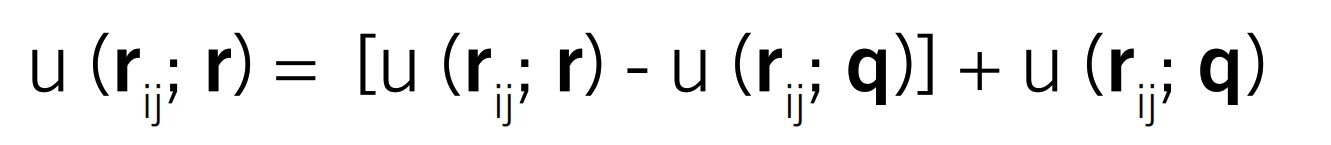Quaderni di progettazione: modellazione dinamica degli ingranaggi. I riduttori trovano largo impiego in numerose applicazioni che spaziano dal settore automobilistico a quello industriale e robotico. Un riduttore epicicloidale è una speciale configurazione cinematica che, sfruttando un portatreno, assicura rapporti di riduzione elevati insieme ad un design molto compatto. Un approfondimento del professor Franco Concli della Libera Università di Bolzano.
I riduttori epicicloidali sono ampiamente utilizzati per le trasmissioni che richiedono un’elevata densità di potenza. Esistono diversi campi di applicazione, inclusi, ma non limitati a, meccatronica, automazione e generazione di energia eolica. Per migliorare la progettazione di nuove soluzioni, per svolgere attività di monitoraggio sui riduttori in esercizio e per la definizione degli interventi di manutenzione, la disponibilità di modelli fisici in grado di descrivere con precisione il comportamento dell’impianto, sia in condizioni nominali che di avaria/danneggiamento rappresenterebbe un ottimo supporto agli ingegneri.
Sono già disponibili in letteratura studi sperimentali e numerici sul comportamento dei riduttori. Tuttavia, mentre gli approcci sperimentali sono validi solo per la configurazione specifica testata, le tecniche numeriche mostrano limitazioni legate all’onere computazionale richiesto. Questo documento presenta un approccio innovativo per la caratterizzazione del comportamento di una trasmissione che è stato applicato, a titolo di esempio, a due diverse configurazioni. Si basa su un approccio ibrido che combina elementi finiti (FE) con formulazioni analitiche.
Più in dettaglio, il solutore calcola separatamente la macro-deformazione dei corpi (soluzione numerica basata su una griglia lasca) e dei contatti (risolti analiticamente evitando la necessità di infittimenti della griglia di calcolo). L‘onere computazionale viene ridotto in modo significativo senza influire sulla precisione dei risultati. Questo approccio è stato utilizzato per indagare e comprendere il comportamento vibro-dinamico di un banco di prova back-to-back (tipicamente utilizzato per la caratterizzazione della resistenza alla fatica superficiale degli ingranaggi) e di un riduttore epicicloidale industriale. I risultati ottenuti per i riduttori sani – non danneggiati – sono stati confrontati con misure sperimentali per entrambe le configurazioni al fine di validare l’approccio ibrido. Una volta validati i modelli, la stessa metodologia è stata utilizzata per studiare gli effetti dei guasti tipici degli ingranaggi e in particolare legati alla fatica superficiale (pitting), sulla risposta vibrazionale del sistema. La capacità di riprodurre l’effetto di un danneggiamento con un modello numerico rappresenta il primo passo indispensabile per lo sviluppo di una strategia di Monitoraggio Strutturale (SHM).
Introduzione alla modellazione dinamica degli ingranaggi
I riduttori sono sistemi meccanici caratterizzati da modalità di guasto peculiari come la flessione al piede dei denti e la fatica superficiale (pitting). Mentre la prima è molto pericolosa e porta a cedimento dell’intero sistema, la seconda è meno critica e legata ad un progressivo degrado del comportamento NVH (Noise, Vibration and Harshness).
Inoltre, va ricordato che in applicazioni specifiche come le turbine eoliche, i riduttori sono spesso i componenti più deboli (guasti gravi stimati generalmente ogni 5 anni [1]). La capacità di modellare il comportamento in tempo reale delle trasmissioni ad ingranaggi in esercizio è molto utile per pianificare gli interventi di manutenzione riducendo i costi e prevenendo danneggiamenti gravi.
Jason Louis Austin [2] ha studiato, mediante approcci numerici, il comportamento di una trasmissione multistadio. Yi Guo et al. [3] hanno studiato la ripartizione del carico in un riduttore per turbina eolica da 750 kW. Kahraman et al. [4] hanno valutato l’influenza della dimensione corpo ruota sulla deformazione dell’ingranaggio. I primi risultati erano promettenti anche se sono state osservate alcune discrepanze. Esperimenti sono stati eseguiti anche da Yongzhi Qu et al. [5] utilizzando sensori di deformazione piezoelettrici applicati vicino al piede dente. Sono state osservate differenze nelle misure tra i fianchi degli ingranaggi danneggiati e quelli non danneggiati. La conoscenza del comportamento del riduttore in diverse condizioni di danneggiamento potrebbe essere utile per impostare un monitoraggio basato su sensori e comprendere il livello di danneggiamento aiutando a pianificare gli interventi di manutenzione.
Lo scopo di questo lavoro preliminare è, da un lato, convalidare l’approccio ibrido analitico-FE e, dall’altro, determinare se la presenza e l’evoluzione di un danneggiament superficiale (pitting) può essere valutata dagli spettri vibrazionali predetti numericamente .
Pertanto, l’attività preliminare è consistita nella definizione e validazione di un approccio in grado di modellare l’effetto dei danni superficiali. In una prima fase sono stati modellati riduttori integri ed i risultati sono stati confrontati con le misure sperimentali. L’analisi numerica delle geometrie selezionate (un banco di prova back-to-back e un riduttore epicicloidale) rappresenta già una dura sfida ingegneristica.
Una volta validati i modelli con i dati sperimentali, il passo successivo è stato la simulazione del sistema in presenza di diversi livelli di danno per comprenderne l’effetto sul NVH.
Riduttori in esame
Per convalidare l’approccio sono state utilizzate due geometrie completamente diverse: un banco di prova back-to-back e un riduttore epicicloidale industriale.
BANCO DI PROVA BACK-TO-BACK
La prima geometria utilizzata (Figura 1) per convalidare l’approccio numerico è stato un banco di prova back-to-back. Questo banco prova, disponibile nei laboratori del Politecnico di Milano, è costituito da due riduttori ad assi paralleli collegati tramite due alberi che formano un anello meccanico chiuso. I riduttori hanno lo stesso rapporto di trasmissione 17/18 ma un diverso numero di denti (rispettivamente 34/36 e 17/18). La riduzione 34/36 (chiamata service) ha ingranaggi elicoidali mentre la seconda (chiamata testing) ha ingranaggi cilindrici.
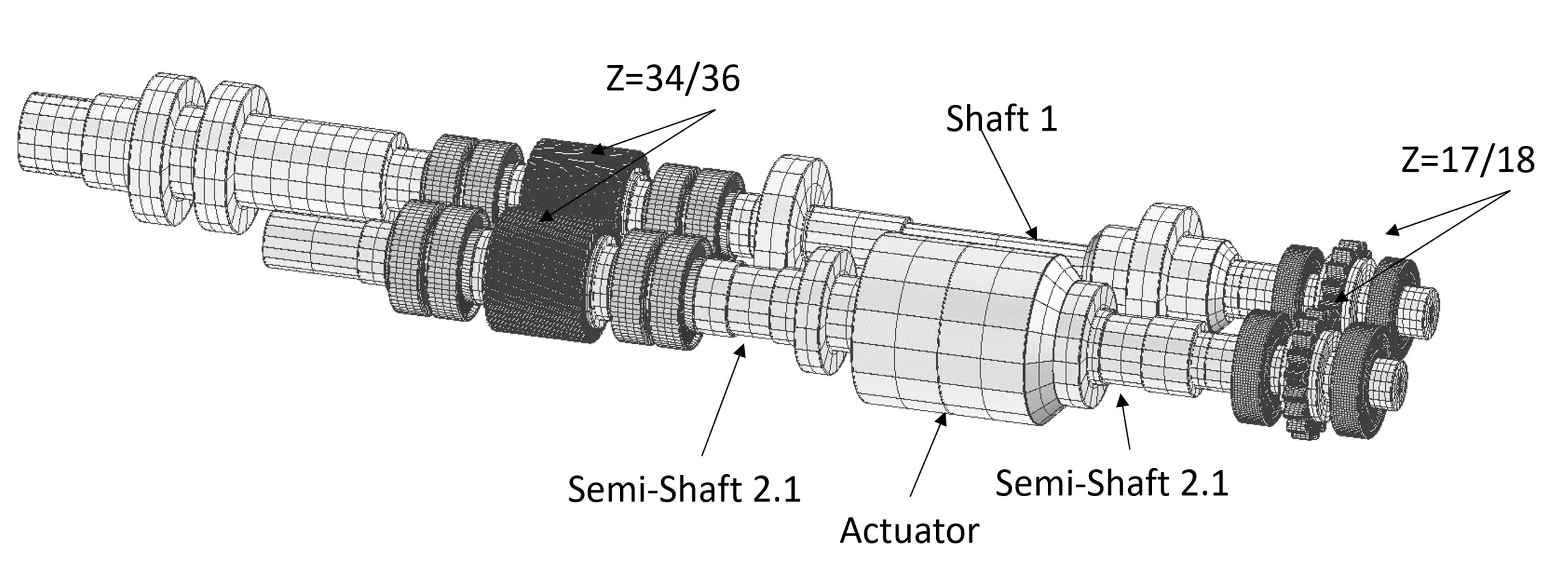
Il carico viene applicato mediante una rotazione relativa dei due semialberi (Figura 1) che collegano i due riduttori (tramite un attuatore idraulico). Il motore elettrico fornisce solo le perdite di potenza (principalmente dovute all’attrito) e non l’intera potenza che scorre nel circuito meccanico.
Ogni ingranaggio del cambio di servizio è supportato da 4 cuscinetti a rulli conici (Figura 2) mentre gli ingranaggi appartenenti al cambio di prova sono supportati da due cuscinetti a rulli.
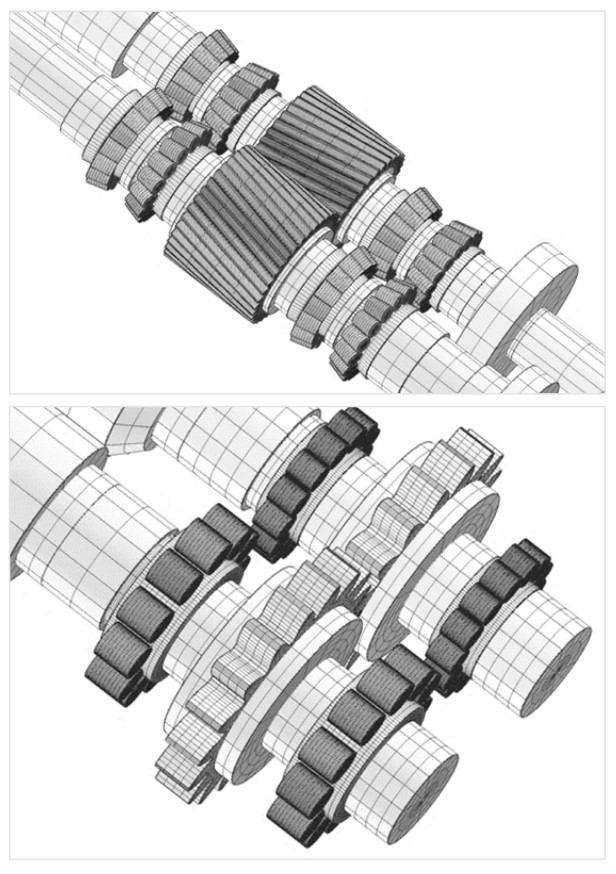
testing (Z17 e Z18);
RIDUTTORE EPICICLOIDALE
Il secondo caso modellato è stato un riduttore epicicloidale monostadio avente un rapporto di riduzione i = 3. Si tratta di un riduttore epicicloidale di precisione a gioco ridotto adatto per applicazioni meccatroniche. L’ingranaggio solare è forzato sull’albero di ingresso (Figura 3) e supportato da un cuscinetto a sfere. Il portatreno (albero di uscita) è supportato, a sua volta, da due cuscinetti a sfera. Tre satelliti interagiscono con l’ingranaggio solare e l’anello esterno. Quest’ultimo è brocciato direttamente nella cassa in ghisa sferoidale [6], [7]. I satelliti sono supportati mediante cuscinetti a rullini a pieno riempimento [8] [9]. I dati completi sono riportati in letteratura [10] – [13].
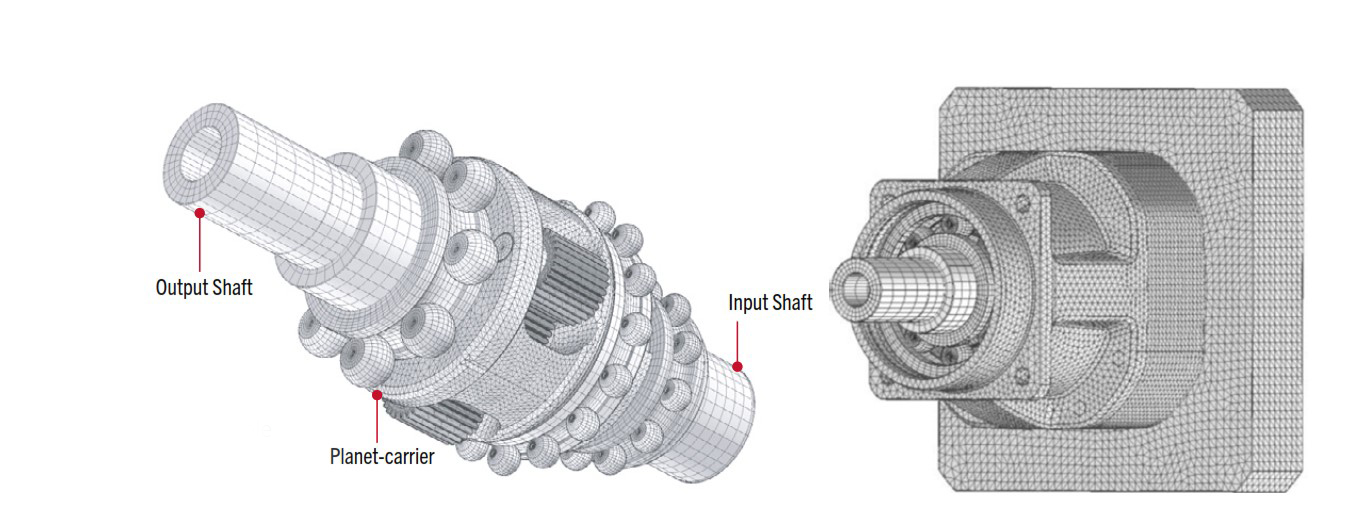
Modellazione numerica degli ingranaggi
La modellazione dei suddetti sistemi ad ingranaggi è stata effettuata sfruttando un innovativo approccio ibrido analitico-FE. Le simulazioni sono state eseguite con il software Transmission3D di ANSOL. Questo è stato specificamente sviluppato per eseguire simulazioni di intere trasmissioni in un ragionevole lasso di tempo. Permette di modellare ingranaggi, cuscinetti (con tutti gli elementi volventi), alberi, casse e gli altri elementi tipici presenti in una trasmissione ad ingranaggi.
Mentre per descrivere la deflessione macroscopica dei componenti viene utilizzato un approccio tradizionale FE, i contatti tra i corpi (cioè denti degli ingranaggi, elementi volventi e piste nei cuscinetti ecc.) sono risolti analiticamente utilizzando la teoria Hertziana.
Un approccio numerico tradizionale richiede, per simulare adeguatamente un contatto, un infittimento della griglia di calcolo per garantire la convergenza della soluzione. Considerando la complessità di un sistema di ingranaggi ed il fatto che la posizione del contatto così come il numero di superfici in presa è variabile durante il funzionamento, con un FEM tradizionale ogni fianco dell’ingranaggio dovrebbe essere discretizzato con una griglia molto fitta portando ad un aumento del numero di equazioni da risolvere. Al contrario, il presente approccio utilizza una griglia relativamente lasca (poche equazioni) in aggiunta ad un’equazione analitica per ogni contatto attivo.
Più nel dettaglio, il primo step è la determinazione dei punti in cui le singole superfici di contatto appartenenti ai due corpi sono più vicine tra loro prima dell’applicazione del carico [14]. Successivamente si determinano le curvature delle superfici. Con queste informazioni, viene stimata la dimensione della zona di contatto utilizzando la teoria Hertziana ed una griglia (più grande dell’ellisse di contatto hertziana prevista) viene disposta attorno a ciascun punto di contatto (Figura 4).
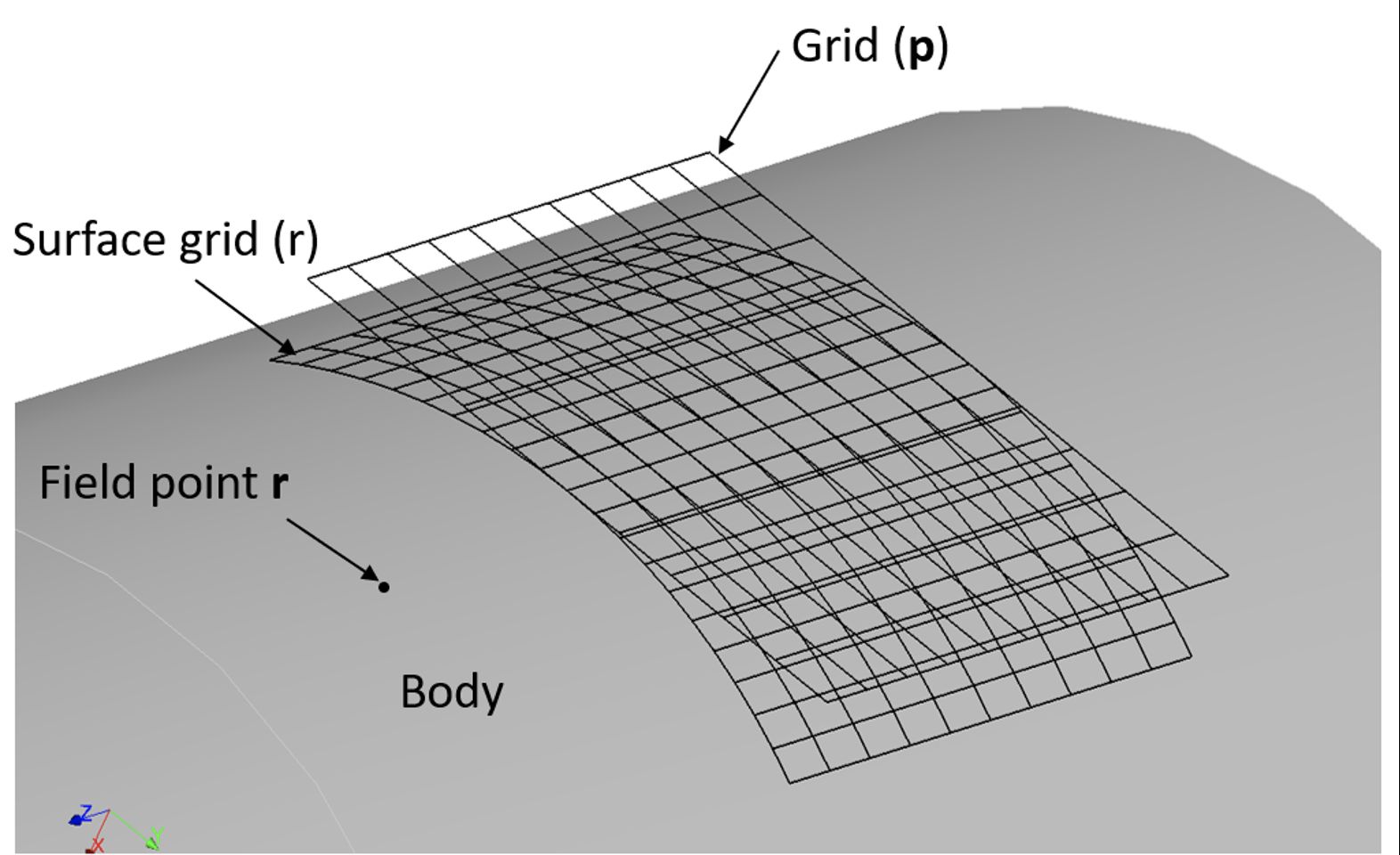
La griglia è quindi proiettata sulle superfici del corpo. Le pressioni di contatto calcolate non risultano essere sensibili alle dimensioni della griglia.
Lo spostamento u (rij; r) di un punto r a causa di un carico nel punto rij può essere espresso come
dove qq è un punto all’interno del corpo sufficientemente distante dalla superficie (Figura 5). Il primo termine, [u(rij; r) and u(rij; q)], viene valutato con un integrale di superficie, mentre il secondo, u(rij; q), viene calcolato numericamente (FEM) [14].
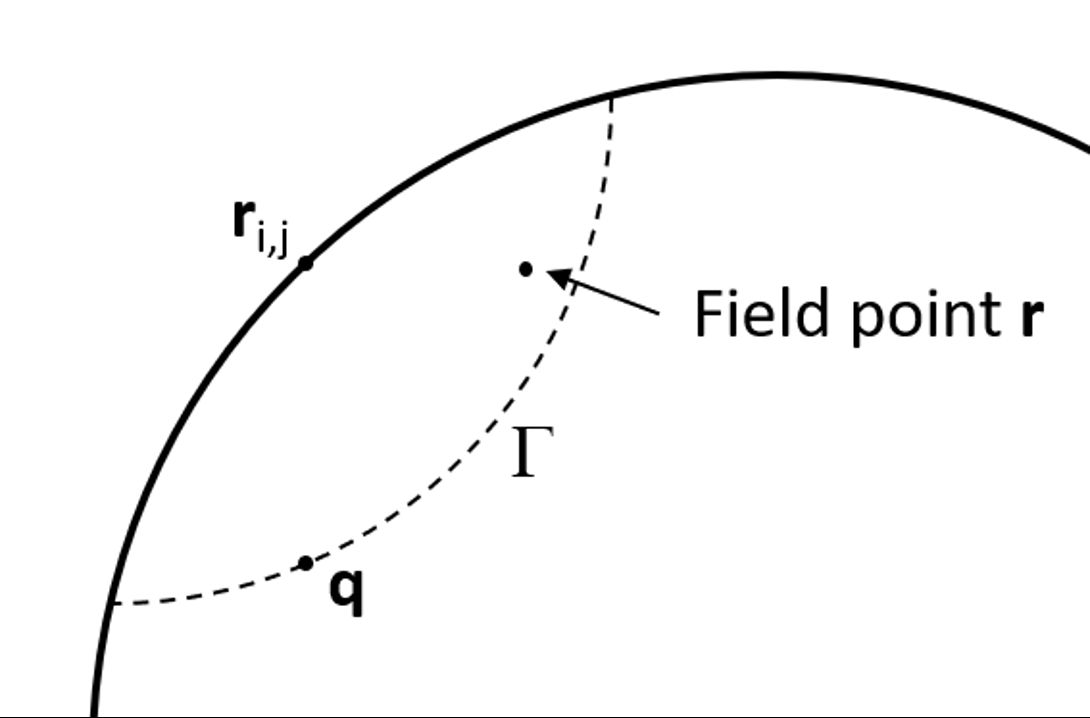
Il termine tra parentesi quadre rappresenta la deflessione di r rispetto al punto q. Questa componente relativa risulta stimata meglio usando la soluzione di Boussinesq [15] piuttosto che i risultati FE. La deformazione del corpo, infatti, non influirà in modo significativo su questo termine. D’altra parte, il termine rimanente u(rij; q) non è significativamente influenzato dalle sollecitazioni locali sulla superficie. Questo a patto che q sia abbastanza lontano dalla superficie. u(rij; q) è stimato tramite modello FE. La posizione di q è chiamata punto di “corrispondenza”. Per far corrispondere l’integrale di superficie e le soluzioni FE si può usare un insieme di punti G invece di un singolo punto q [16]. Ulteriori dettagli sono forniti in [17].
Sebbene questo approccio si sia dimostrato significativamente più efficiente dal punto di vista computazionale rispetto ai FEM tradizionali, sono possibili ulteriori miglioramenti: un modello ancora più snello è stato ottenuto sostituendo i cuscinetti con molle radiali equivalenti aventi una rigidezza equivalente ottenuta da simulazioni preliminari di stato stazionario.
Miglioramenti delle prestazioni
La configurazione planetaria utilizzata in questo studio è stata modellata anche con un approccio FEM tradizionale. Un confronto tra l’onere computazionale richiesto dall’approccio tradizionale e quello dell’approccio attuale sullo stesso hardware (115GFLOPS) ha evidenziato come quest’ultimo sia circa 700 volte più rapido se i cuscinetti vengono modellati e 2000 volte più veloce se vengono utilizzate le molle equivalenti. Mentre una simulazione quasi statica con l’approccio tradizionale richiede circa 30 ore, il tempo di simulazione di un singolo istante temporale richiede meno di un minuto con l’approccio ibrido.
Misure sperimentali
I test sul banco di prova back-to-back sono stati eseguiti a una velocità di rotazione di 3000 rpm (GMF17 / 18 = 850 e GMF34 / 36 = 1700 Hz) senza carico applicato. Un accelerometro montato sul riduttore di prova ha consentito la misurazione delle vibrazioni durante il funzionamento (Figura 1).
L’architettura planetaria è stata testata su un banco di prova elettrico a circuito chiuso composto da un motore elettrico, un generatore e due inverter. L’ingranamento dei denti (GMF = 1800 Hz) era la principale fonte di eccitazione. Le vibrazioni sono state misurate per mezzo di due accelerometri piezoelettrici (PCB M352C68) fissati sulla cassa del riduttore tramite supporti magnetici (Figura 2).
Validazione dei modelli
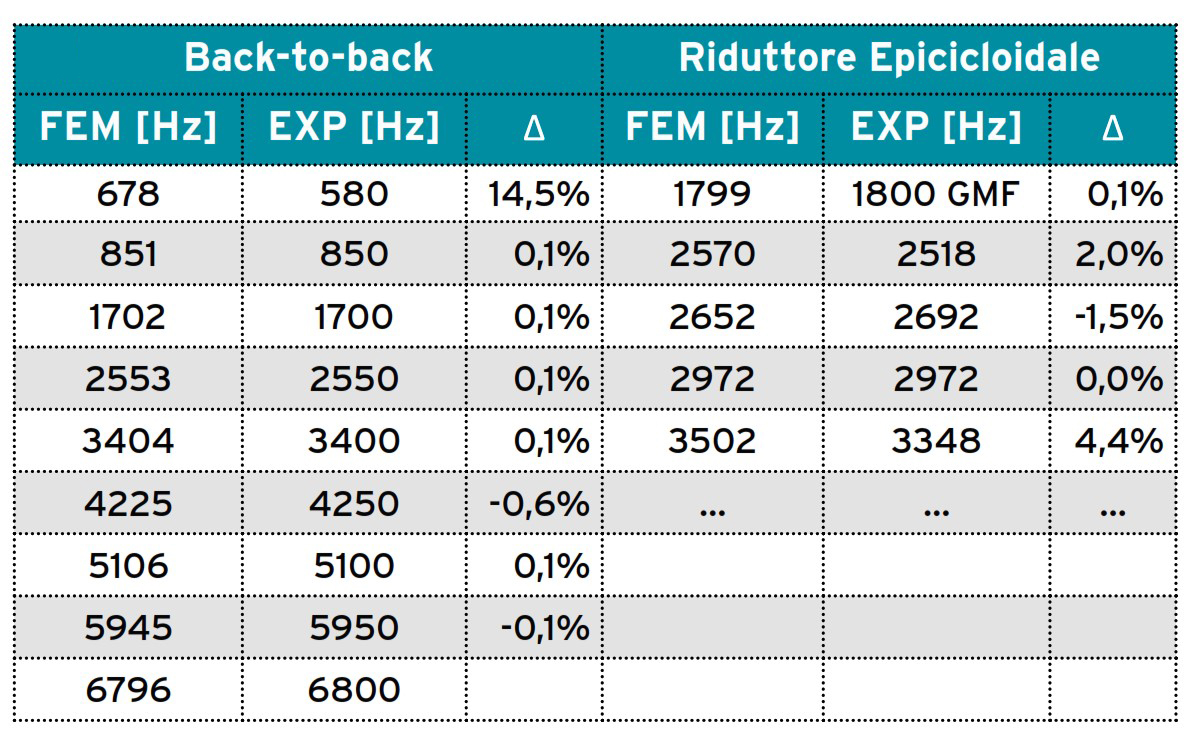
La tabella sottostante mostra il confronto tra i dati numerici e sperimentali per il banco prova back-to-back e per il riduttore epicicloidale.
Per l’architettura back-to-back, i picchi principali appaiono intorno a 850 Hz e 1700 Hz (frequenze di ingranamento delle due coppie di ingranaggi). Gli altri picchi sopra il GMF (2550, 3400 ecc.) sono armoniche delle frequenze di ingranamento. Il primo picco intorno a 600 Hz è una frequenza propria del banco. La concordanza tra le frequenze calcolate e misurate è buona, tranne per questa prima frequenza dove è stata osservata una discrepanza di circa il 15%. Ciò è probabilmente dovuto a una modellazione non perfetta dell’inerzia del motore elettrico.
Anche per il riduttore epicicloidale il confronto delle frequenze eccitate ha evidenziato la bontà del modello numerico.
Spettro vibrazionale in presenza di danneggiamenti
Dopo che l’approccio è stato validato, nei modelli numerici sono stati introdotti i danneggiamenti. Al fine di comprendere l’effetto di un danneggiamento superficiale sullo spettro vibrazionale, sono state eseguite simulazioni aggiuntive su entrambe le configurazioni includendo danneggiamenti che differivano per grado e posizione. In questa fase, il danneggiamento è stato modellato su un solo dente. La presenza di danneggiamenti produce una modifica del modello di contatto. A titolo di esempio, le pressioni di contatto risultanti sul fianco di un dente sono mostrate in Figura 6 sia per un fianco sano che per uno danneggiato.
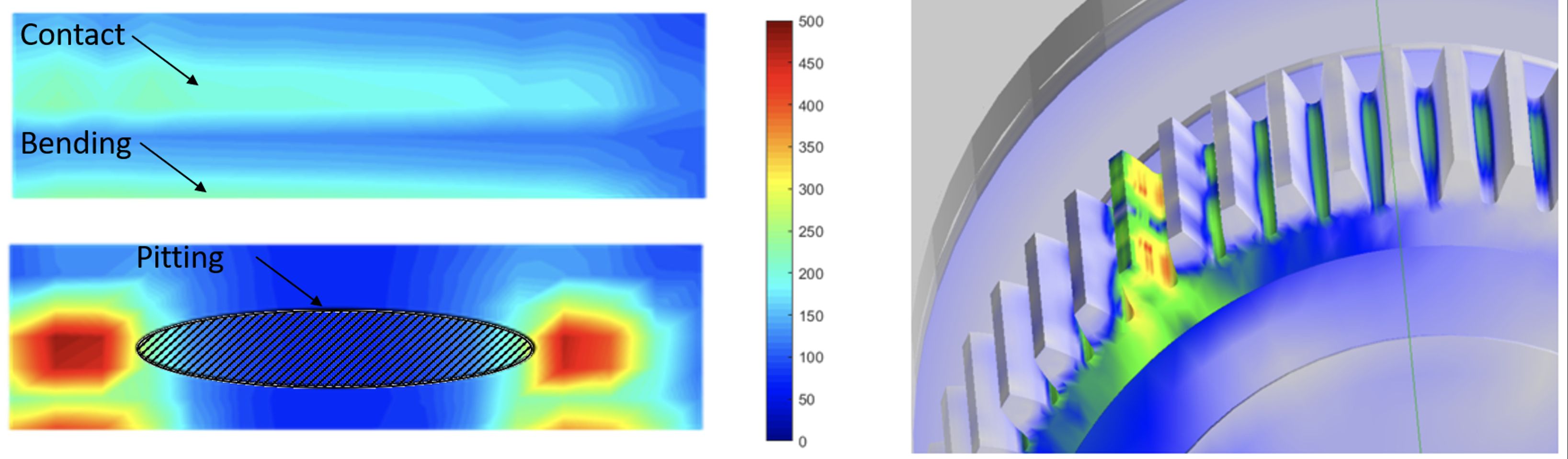
Nella parte superiore di Figura 6, che corrisponde a un dente non danneggiato, la regione sollecitata è dovuta al contatto dell’ingranaggio e legata allo sforzo di flessione. Le sollecitazioni sono abbastanza uniformi e le piccole differenze lungo la direzione assiale sono dovute alla deformazione del portatreno. La parte inferiore di figura 6, che corrisponde a un dente danneggiato, mostra una regione centrale non è caricata mentre la restante porzione del fianco è sovraccaricata.
Anche se lo stato di sollecitazione (e di deformazione) rappresenta un’indicazione del danneggiamento, in questa fase iniziale solo le vibrazioni, più facili da misurare, sono state considerate come trigger.
Figura 7 e 8 mostrano i risultati delle simulazioni numeriche transitorie del banco di prova back-to-back per due diversi livelli di danneggiamento e in condizioni integre in termini di accelerazioni (vibrazioni). I risultati sono riportati sia nel dominio del tempo che nel dominio della frequenza.
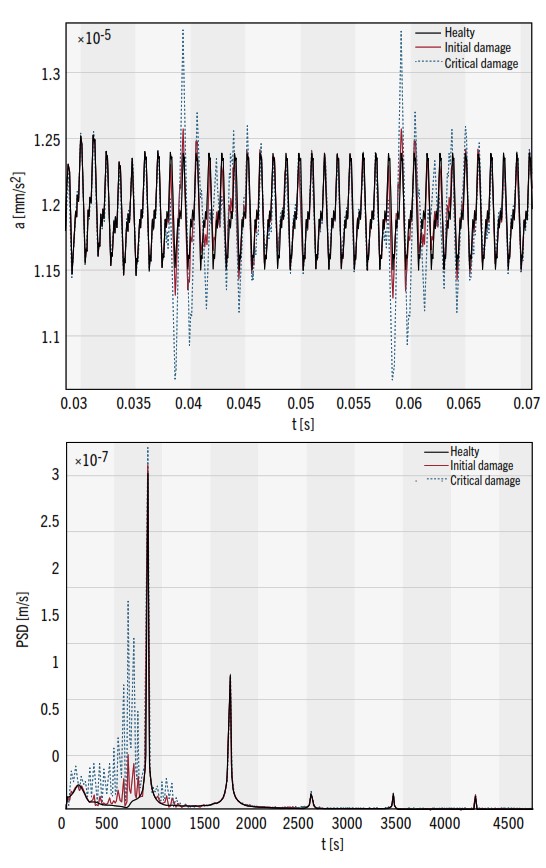
danneggiamento
Gli spettri mostrano come la presenza di pitting non moduli la frequenza di ingranamento e le sue armoniche: tuttavia la nucleazione e la progressione del danneggiamento favoriscono l’eccitazione di frequenze aggiuntive.
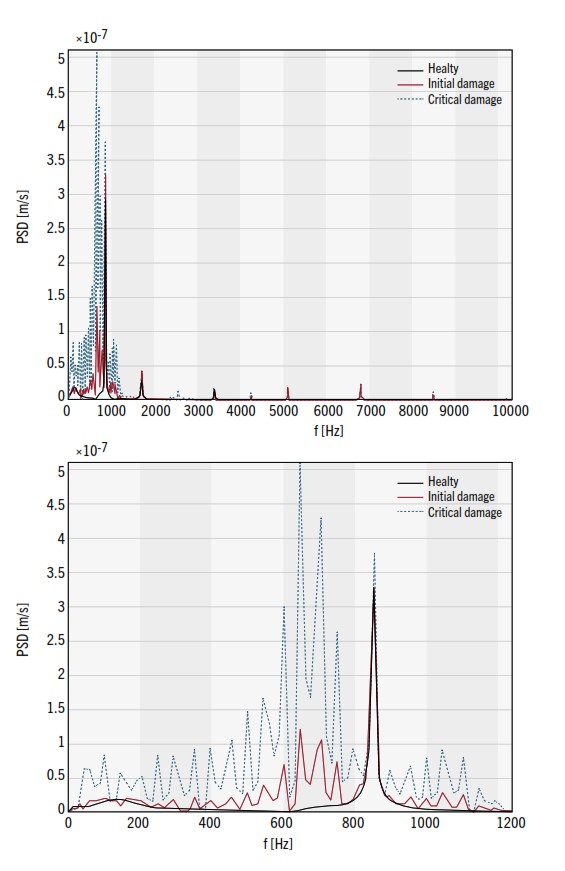
differenti livelli di danneggiamento
Questa evidenza può essere una caratteristica importante nello sviluppo di un algoritmo SHM per la valutazione dello stato di salute dei riduttori [18] – [21] ma, al fine di definire meglio la relazione quantitativa tra la gravità del danno e dell’effetto prodotto e definire le soglie corrispondenti, sono necessarie alcune attività aggiuntive.
Modellazione dinamica degli ingranaggi: conclusioni
È stato proposto un nuovo approccio ibrido analitico-FEM per la simulazione di sistemi ad ingranaggi, anche complessi. Sono state effettuate simulazioni iniziali della configurazione reale, ovvero comprensiva di cuscinetti, per calcolare le rigidezze dei supporti. Con questi risultati sono stati costruiti modelli più snelli in cui tutti i supporti sono stati sostituiti con molle radiali equivalenti utilizzati per modellare un banco prova back-to-back e un riduttore epicicloidale industriale.
I risultati delle simulazioni transitorie in termini di spettri vibrazionali sono stati confrontati con misurazioni sperimentali per entrambe le configurazioni, mostrando un buon accordo.
Per il banco di prova back-to-back, l’effetto della presenza di pit sugli spettri vibrazionali è stato studiato utilizzando un approccio numerico: le simulazioni hanno evidenziato come i difetti favoriscano l’eccitazione di frequenze aggiuntive (principalmente al di sotto del GMF). Questo fenomeno aumenta con la gravità del danno. Tuttavia, una relazione quantitativa deve ancora essere determinata. Per quanto riguarda il set di ingranaggi planetari, i risultati delle prime simulazioni in condizioni ”sane” sono promettenti, ma ancora da affinare.
Sono in corso ulteriori studi, al fine di completare l’attività, con l’obiettivo di mettere a punto i modelli numerici e di comprendere meglio la relazione quantitativa tra danno e spettri di frequenza. L’obiettivo finale è l’estensione di una strategia SHM per gli ingranaggi.
Riconoscimenti
Questo lavoro è supportato dal progetto RTD 2018 – SMOG Structural Health Monitoring of Mechanical gearboxes finanziato dalla Libera Università di Bolzano (PI: Franco Concli).
Gli autori desiderano ringraziare il Dr.Ing. PhD. Giorgio Bonori, responsabile di Transmission3D per l’Europa per l’aiuto fornito durante tutta la durata del progetto e per la licenza didattica del software.