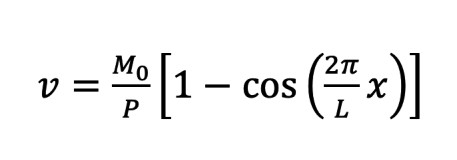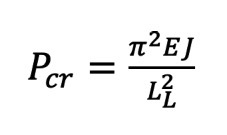L’instabilità elastica è un meccanismo caratteristico delle strutture snelle che porta a cedimenti anche quando le sollecitazioni nel componente sono ben al di sotto del limite elastico.
Un componente meccanico soggetto a carichi di tipo statico può cedere anche a fronte di un meccanismo differente da quello legato al superamento dei limiti di resistenza (snervamento o rottura) del materiale di cui è costituito. Un esempio in tal senso è quello di un cedimento tipico di strutture soggetti a carichi compressivi e detto per instabilità elastica.
Tale tipologia di cedimento è particolarmente gravosa in quanto si manifesta anche a carichi inferiori a quelli limite caratteristici del materiale in oggetto. Inoltre, questo tipo di cedimento avviene solitamente in modo improvviso. Esempi di componenti meccanici che storicamente manifestano questa tipologia di problema sono le bielle, le molle ad elica, gli ingranaggi a vite etc..
Ciò che accomuna questi organi di macchina è la loro caratteristica snellezza, per cui, in presenza di un sufficiente carico compressivo, si ha un’inflessione trasversale (fenomeno di sbandamento o buckling).
Il carico massimo che il componente può sopportare prima di cedere per instabilità è chiamato carico critico e solitamente indicato con Pcr. Ogni valore superiore a tale carico provoca, per quel componente, il cedimento per buckling.
Carico critico di Eulero per le travi snelle
Il caso più semplice di elementi che possono cedere per instabilità da carico di punta è rappresentato dalla cosiddetta asta di Eulero. Ipotizzando che la trave in oggetto risulti omogenea, isotropa e perfettamente rettilinea, che il carico (compressivo) sia perfettamente assiale, che lo stato di sollecitazione della trave sia puramente elastico e che l’inflessione si abbia su un unico piano, è possibile derivare una espressione matematica in grado di descrivere queta tipologia di cedimento. Si consideri lo schema questa figura
se il carico (P) rimane al di sotto del carico critico (Pcr), l’asta resterà rettilinea, in caso contrario si avrà una sua deflessione.
Si consideri ora la condizione limite per cui P è appena superiore al carico Pcr. In queste condizioni, anche una forza radiale F di piccolissima entità (disequilibrio) porta subito ad una deformazione della trave, che oltretutto rimarrà deformata anche a seguito della rimozione della forza F. Al contrario, una piccola riduzione del carico assiale P tale per cui P < Pcr, porterà subito al raddrizzamento della trave e scomparsa della deformazione.
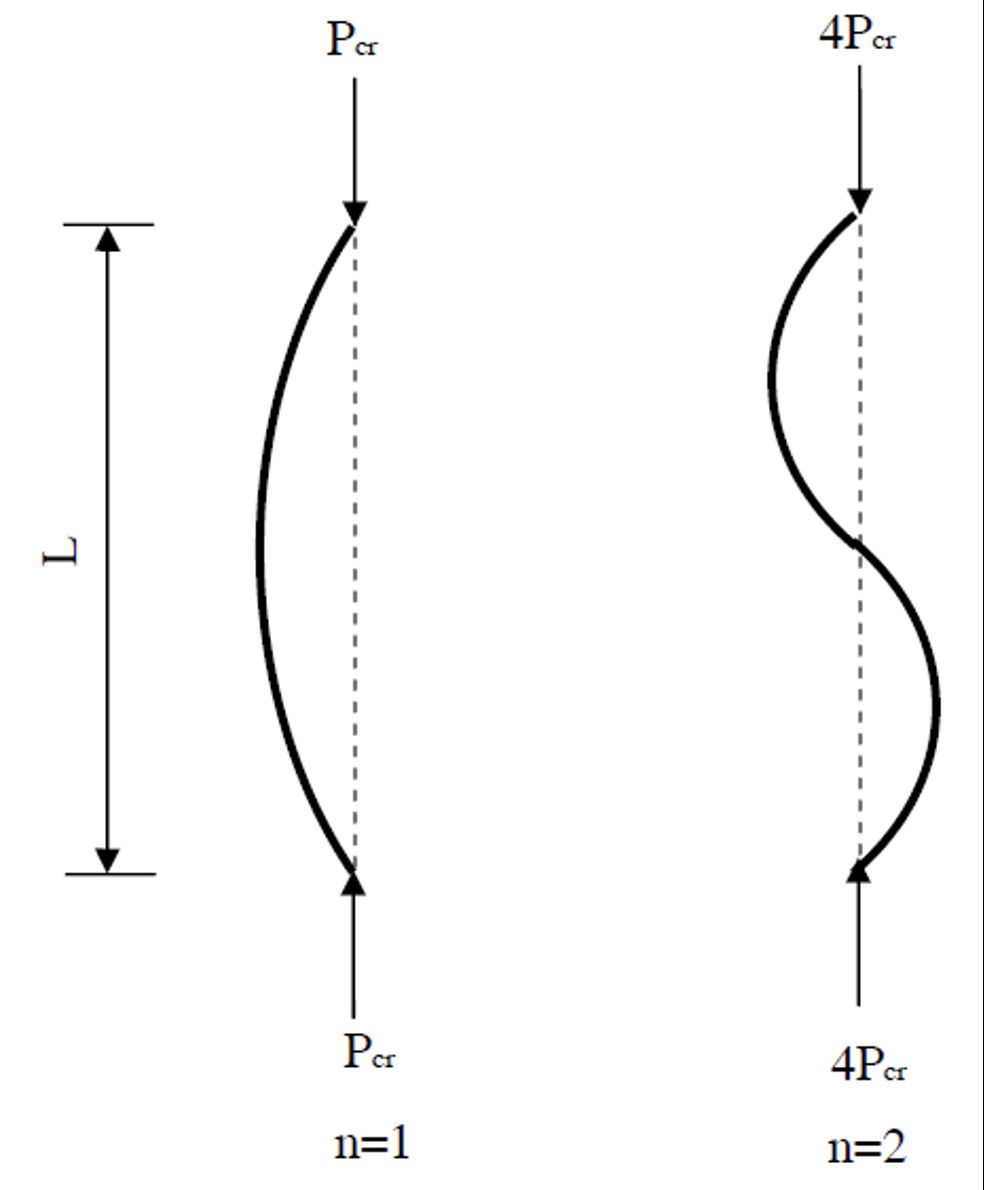
Per descrivere matematicamente questa evidenza è possibile basarsi sull’equazione della linea elastica. Per una trave sorretta da due appoggi (cerniera carrello) e caricata assialmente, tale equazione differenziale del secondo ordine ammette una soluzione per lo spostamento v che, considerando che in corrispondenza delle cerniere tale spostamento deve risultare nullo, risulta essere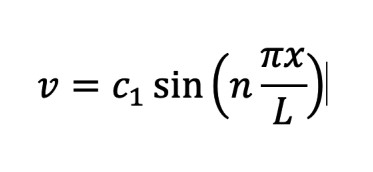
In cui L è la lunghezza della trave mentre n è un numero intero detto numero di semionde. La costante C1 rappresenta la massima inflessione della trave.
Il valore minimo di P, detto Carico Critico Euleriano, si ha con n=1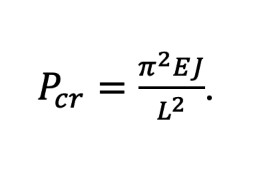 
Questo è il carico minimo per cui l’asta può risultare soggetta a deformazione per instabilità. n pari a 1 significa che la deformata sarà semplicemente un arco di cerchio passante per i due punti, ovvero formerà una sola semionda. Viceversa, con n=2, il valore del carico critico quadruplica ma si possono avere deformate con una doppia onda (sinusoide completa).
Si noti come il valore del carico critico non dipenda dalle caratteristiche di resistenza del materiale con cui è realizzata la trave ma solo da lunghezza L, dalle proprietà inerziali J e modulo di elasticità E. Dalla formula di Eulero è anche facile intuire come l’instabilità di avrà nel piano con proprietà inerziali minime. Da qui è immediato intuire come mai spesso le colonne abbiano sezione circolare (momenti di inerzia bilanciati).
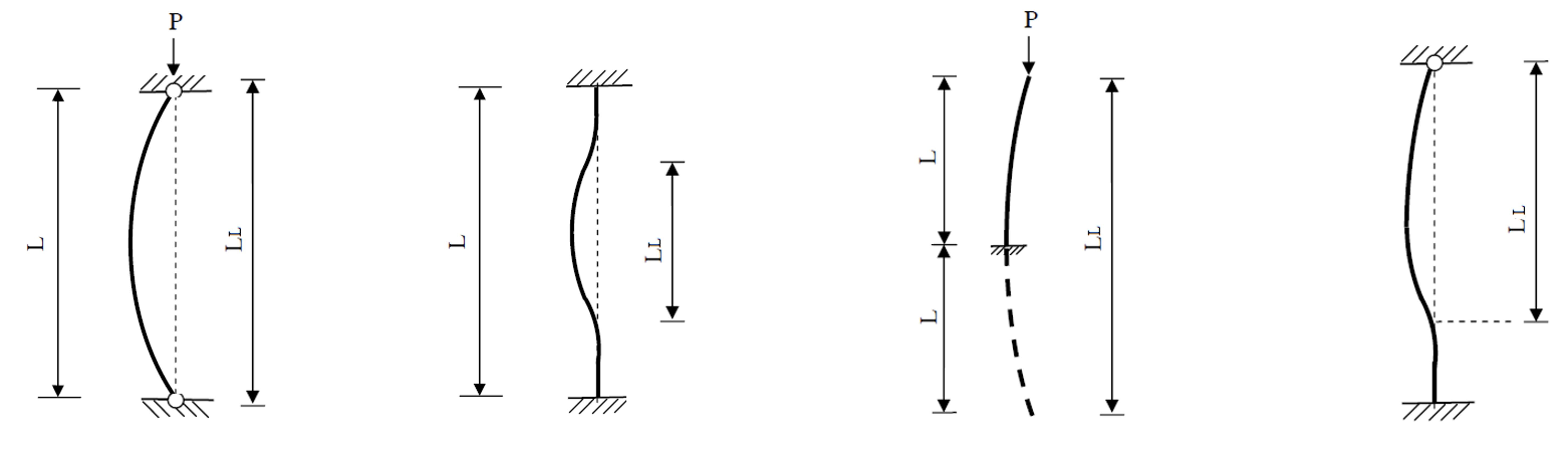
Allo stesso modo di quanto fatto per un’asta con doppio appoggio, è possibile, partendo dall’equazione della linea elastica, determinare la soluzione in termini di inflessione v per un’asta con doppio incastro che risulterà
in cui M0 è la relazione vincolare data dall’incastro. In questo caso, il carico critico risulta
con LL=½L. LL è detta lunghezza libera di inflessione, e rappresenta la distanza tra due punti in cui il momento flettente risulta nullo. Nel caso di trave incastrata ad un’estremità e appoggiata (libera di ruotare) all’altra, la lunghezza libera di inflessione risulta LL=L/√2. Infine, una trave incastrata solamente ad un’estremità avrà una lunghezza libera di inflessione pari a LL=2L.
Conclusioni
Sebbene l’instabilità sia un fenomeno che coinvolge solamente componenti snelli soggetti a carichi compressivi, è buona norma in fase di progettazione verificare che i carichi massimi non superino quelli critici e garantire alla struttura la stabilità.
