I nastri trasportatori sono impiegati in tutto il mondo per il trasporto di passeggeri, merci generiche e materiali da circa 250 anni. Sono impiegati in larga misura nel settore minerario, in cementifici, centrali elettriche, produzione chimica e movimentazione industriale in genere. Negli ultimi decenni lo sviluppo delle tecnologie di progettazione dei nastri trasportatori ne ha accresciuto velocità, portata e capacità.
di Giorgio De Pasquale, Elena Perotti, Giorgio Avanzato
Rispetto ad altri metodi di trasporto, i nastri trasportatori sono vantaggiosi nel caso di grandi volumi in modo rapido ed efficiente anche su lunghe distanze e in aree dove strade e infrastrutture ferroviarie sono insufficienti. Oggi sono utilizzati nastri trasportatori sia in ambito indoor sia come alternativa ai trasporti via terra in esterno. La maggior parte degli impianti ha lunghezza variabile fra 10 e 20.000 m e larghezza variabile fra 0.3 e 3.2 m. La velocità può raggiungere i 9 m/s e la portata può superare le 40.000 t/h.
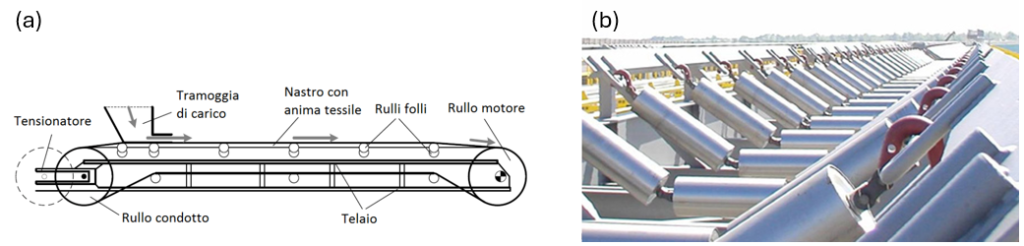
Il sistema è normalmente basato su un nastro in polimero rinforzato da un’anima tessile ed è possibile adottare rinforzi longitudinali mediante cavi d’acciaio per le applicazioni più critiche. Come si vede in Figura 1a, il nastro è montato fra due tamburi, uno motorizzato e uno trascinato; il nastro è poi supportato per tutta la sua lunghezza da rulli rotanti che ne mantengono la planarità e sostengono il peso del materiale trasportato. Un dispositivo mobile, detto tensionatore, applica il precarico longitudinale sul nastro per consentire la trasmissione senza strisciamento fra nastro e rullo motore e per evitare l’allentamento e abbassamento del nastro lungo la linea. Il nastro può essere arrestato mediante lo stesso motore oppure mediante un freno di emergenza. Le rulliere possono avere forme concave per il trasporto di materiali non compatti (Figura 1b).
Come per ogni sistema, anche per i nastri trasportatori l’affidabilità complessiva è data dalla combinazione delle affidabilità dei singoli componenti. Il malfunzionamento di uno dei componenti può portare a costosi tempi di fermo in caso di arresto totale del sistema, fino all’interruzione del processo di produzione dell’impianto industriale.
Il nastro rappresenta il componente con maggiore valore aggiunto del sistema (esso costituisce in media i 2/3 del valore complessivo) ed è anche il componente maggiormente soggetto a usura e deterioramento a causa del contatto con il materiale trasportato, alle sollecitazioni meccaniche e al contatto con i rulli per la trasmissione della potenza di avanzamento. Si evidenzia quindi, fin da subito, che l’incremento dell’affidabilità complessiva passa dalla implementazione di efficaci sistemi di monitoraggio dello stato di salute del nastro, i quali sono l’oggetto principale delle attuali attività di ricerca in questo settore, come quelle condotte presso lo Smart Structures and Systems Lab del Politecnico di Torino (www.s3laboratory.com).
Evoluzione della progettazione e delle normative
Le prime norme per il calcolo di potenza e forze
Nel dopoguerra, nonostante l’ampia diffusione dei nastri trasportatori, non esistevano norme condivise che definissero un metodo per il dimensionamento e la progettazione di questi impianti.
Fu per prima la Conveyor Equipment Manufacturer’s Association (CEMA) a sviluppare e pubblicare nel 1966 un documento che fornisse a tutto il mondo una guida per la progettazione dei trasportatori a nastro [1]. Essa consisteva in una serie di equazioni per il calcolo della potenza necessaria all’impianto e delle forze in gioco sul nastro, in funzione delle dissipazioni che si sviluppano all’interno del sistema quali, ad esempio, l’attrito dovuto al rotolamento dei rulli, il cambio di quota del materiale e del nastro in caso di dislivelli, gli attriti nelle varie pulegge e tenditori.
Successivamente in Europa furono diffuse altre due norme che indicavano procedure simili a quelle della CEMA. La prima fu la ISO 5048 nel 1979 e la seconda fu la DIN 22101 nel 1982. In queste norme il nastro viene considerato come un corpo rigido, pertanto, attraverso la dinamica del corpo rigido newtoniano, è possibile determinare le forze scambiate con i sistemi con cui entra in contatto [2]. L’obiettivo è quello di calcolare la forza necessaria per il moto del nastro attraverso una analogia elettrica. I punti di contatto del nastro con altri corpi, come ad esempio i rulli, o il dislivello da superare, rappresentano delle resistenze. Sommando tutte le resistenze si riesce a calcolare la forza massima per il movimento del nastro.
Le norme citate hanno come obiettivo quello di determinare in primis la forza effettiva e la potenza del motore necessaria, però ciò che le contraddistingue è l’uso differente dei coefficienti di attrito: la DIN utilizza un coefficiente globale mentre la CEMA dei coefficienti diversi per nastro, rulli e tamburi [3].
L’estensione alla dinamica e agli elementi finiti
L’approccio scelto dalle prime norme può essere considerato come “quasi-statico” poiché non prende in considerazione molti fenomeni dinamici che hanno luogo durante il normale funzionamento del nastro trasportatore. Nel caso di sistemi di piccole dimensioni e con bassi carichi, una ottica di progettazione di tale tipo può essere considerata accettabile poiché conduce a risultati in grado di descrivere discretamente il comportamento del sistema. In tutti gli altri casi sono invece presenti effetti che non è possibile trascurare in fase di progettazione.
Esempi di questi effetti sono, ad esempio, la variazione della coppia motrice e dell’accelerazione che influenzano gli sforzi sul nastro, i disallineamenti del nastro che comportano un aumento della resistenza all’avanzamento, il danneggiamento progressivo di alcuni componenti, le interruzioni non programmate del processo, etc. Per tutti questi casi, è stato necessario integrare alle norme originarie anche gli aspetti dinamici del sistema, in modo da analizzarne meglio il funzionamento e soprattutto potendo simulare transitori di non-stazionarietà come l’avviamento o l’arresto forzato del sistema che in alcuni casi sono proprio le fasi più critiche.
Nacque così la necessita di sviluppare dei modelli analitici dai quali fosse possibile estrarre informazioni più dettagliate sugli effetti dinamici sul nastro. In Germania tra gli anni ‘70 e ‘80 del Novecento fu sviluppato un primo modello ad elementi finiti [2]. La prima innovazione nel calcolo è stata rappresentata dalla divisione del tratto di andata e ritorno del nastro, mediante una discretizzazione in due elementi. Da questa considerazione, parallelamente allo sviluppo di metodi di calcolo più efficiente e rapidi, si osservò come la discretizzazione in più elementi portasse a risultati più accurati. I primi elementi erano monodimensionali e includevano sia le proprietà elastiche sia quelle viscose del nastro. Essi possono essere rappresentati attraverso l’analogia elettro-meccanica come una molla e uno smorzatore in parallelo [4].
Gli effetti trasversali sul nastro
I modelli monodimensionali citati erano in grado di interpretare gli effetti di deformazione statica e dinamica del nastro in direzione assiale, l’unico grado di libertà considerato. Altri effetti piuttosto importanti, come la flessione del nastro, la sua deformazione lungo il contatto con il tamburo, le sue vibrazioni in direzione trasversale sono stati studiati solo in seguito. Le vibrazioni trasversali del nastro possono ridurre le prestazioni del sistema o causare usura accelerata del nastro. Si comprende il notevole interesse nello sviluppo di modelli per la dinamica trasversale e per l’analisi dei parametri di funzionamento del sistema che più influenzino le vibrazioni trasversali del nastro [5].
Altri studi volti al miglioramento della progettazione sono stati orientati alla trasmissione del moto tra nastro e tamburo e ai fenomeni che ne regolano il meccanismo. In particolare, è stato notato che la trasmissione di potenza tra questi due elementi avviene grazie agli sforzi e alle deformazioni a taglio e non a causa di una semplice deformazione assiale come si pensava prima [6].
Un interessante ambito di ricerca dell’ultimo decennio è l’ottimizzazione energetica da affiancare alla progettazione. Dato l’elevato utilizzo in termini orari degli impianti a nastro trasportatore all’interno delle industrie, è essenziale contenere al massimo i consumi tramite un miglioramento progressivo della efficienza del sistema. Di conseguenza, analizzare il funzionamento dei sistemi a nastro e definire le condizioni di lavoro che permettano di ridurre i consumi di energia, sono attualmente gli obiettivi primari.
Modelli dinamici
La progettazione dell’impianto deve tenere conto degli aspetti inerenti la dinamica del sistema. Durante i transitori di avvio, arresto o sovraccarico, infatti si verificano le condizioni di lavoro più critiche che possono causare scorrimento indesiderato nastro-tamburo, rotture del nastro o altri problemi di funzionamento.
Per questo tipo di analisi, il progettista deve utilizzare modelli opportuni, basati su diagrammi di corpo libero di porzioni del sistema. Viene analizzato ogni elemento del sistema e la modalità attraverso cui avviene la trasmissione del moto tra un elemento e l’altro, in modo da ricavare le leggi fisiche che ne governano le relazioni. L’elemento più complesso da analizzare è sicuramente il nastro, poiché esso rappresenta allo stesso tempo l’elemento fondamentale del sistema, sia quello più critico in fase di funzionamento.
Dinamica del tamburo motore
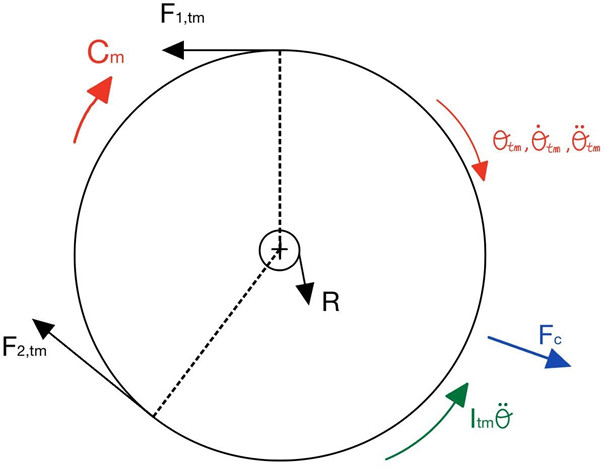
Per analizzare il comportamento dinamico dei tamburi e dei rulli, è necessario costruire il loro diagramma di corpo libero. In Figura 2 è rappresentato il diagramma di corpo libero del tamburo motore e del nastro avvolto su di esso. Nel diagramma sono riportati i carichi agenti sui due elementi, come di seguito dettagliato.
- F1,tm e F2,tmsono le tensioni relative a due sezioni del nastro. Con il pedice 1 si indica la forza “entrante”, corrispondente al primo punto di contatto tra nastro e tamburo. Con il pedice 2 si indica la forza “uscente”, il nastro in tale sezione lascia il tamburo motore e si dirige verso l’altro componente del sistema;
- R è la reazione vincolare al perno. Essa non è centrata rispetto al tamburo e per tale ragione produrrà un momento attorno al centro in verso opposto al verso di rotazione del tamburo. Tale coppia prodotta è Catt;
- Fc è la forza centrifuga agente sulla parte di nastro aderente al tamburo che ruota insieme ad esso con la medesima velocità angolare. Essa non genera una coppia rispetto al centro del tamburo ma influisce sul calcolo della reazione vincolare al perno;
- Cm è la coppia motrice applicata al tamburo dal motore;
- Itm è l’inerzia rotazionale del tamburo motore;
- θ è l’angolo di rotazione del tamburo motore;
Dunque, l’equazione di equilibrio alla rotazione rispetto al centro del perno è la seguente:

Il termine (F1,tm-F2,tm)rtm rappresenta la coppia trasmessa dal nastro al tamburo, che chiameremo Cn-tm.
Dinamica del tamburo condotto
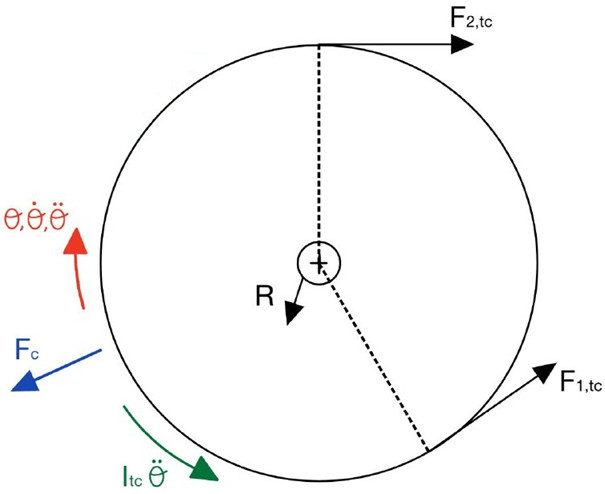
Le medesime considerazioni possono essere applicate agli altri componenti rotativi: il tamburo condotto e i rulli di supporto. Nel caso del tamburo condotto non vi è nessuna coppia esterna che fornisce al tamburo la potenza necessaria alla rotazione, la quale viene conferita dal nastro, il quale aderisce alla circonferenza esterna del tamburo causandone la rotazione. Con riferimento alla Figura 3 si riconoscono i seguenti contributi.
- F1,tc e F2,tc sono le tensioni relative a due sezioni del nastro, in questo caso poiché il nastro deve fornire una coppia concorde al verso di rotazione, la F2,tc è la maggiore delle due;
- Fc è la forza centrifuga agente sulla parte di nastro aderente al tamburo che ruota insieme ad esso con la medesima velocità angolare;
- R è la reazione vincolare al perno che genera la coppia di attrito Catt;
- Itc è l’inerzia rotazionale del tamburo condotto.
L’equazione di equilibrio dinamico alla rotazione attorno al centro del perno è la seguente:

Nastro: modello ad elementi finiti
Il nastro è l’elemento più complesso del sistema. Mentre per gli elementi precedenti, semplici equazioni differenziali di equilibrio di forze e momenti sono sufficienti per descrivere le variazioni di carichi e velocità nel sistema, non è così per il nastro. Infatti sono proprio le sue proprietà reologiche ad influenzare notevolmente la dinamica del sistema.
Nel corso degli anni tantissime analisi e metodi sono stati eseguiti per lo studio della fisica di questo elemento. I vari modelli utilizzati combinano sistemi di molle e smorzatori in serie e in parallelo, in modo da trovare la combinazione tra questi due elementi che meglio simuli il comportamento viscoelastico del materiale. Maggiore è il numero di elementi inseriti, maggiore è il numero di parametri, e quindi anche la complessità delle equazioni che ne derivano.
La tipologia di modello del nastro da considerare varia in base agli obiettivi dell’analisi che ci si pone. Si possono ad esempio considerare come trascurabili gli effetti flessioni e di taglio ed utilizzare un modello a due parametri composto da una molla e uno smorzatore in parallelo. È il modello di “Kelvin-Voigt”, il quale è mostrato in Figura 4.
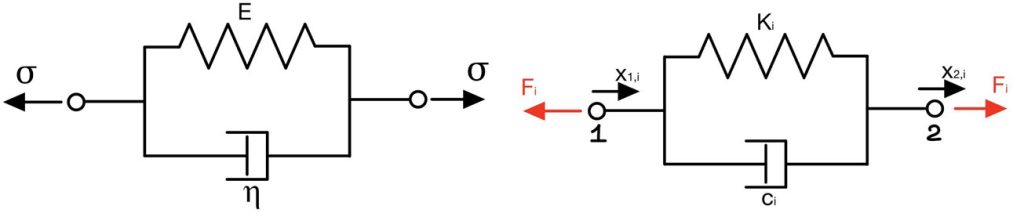
Tale modello considera sia l’effetto di una rigidezza assiale sia la dissipazione viscosa causato dal comportamento viscoelastico del nastro. In termini di forza, si può calcolare quindi, ai capi del tratto di nastro così modellizzato:

in cui ki rappresenta la rigidezza assiale del nastro, ci il coefficiente di smorzamento assiale del nastro e x è la coordinata assiale ai capi del tratto di nastro.
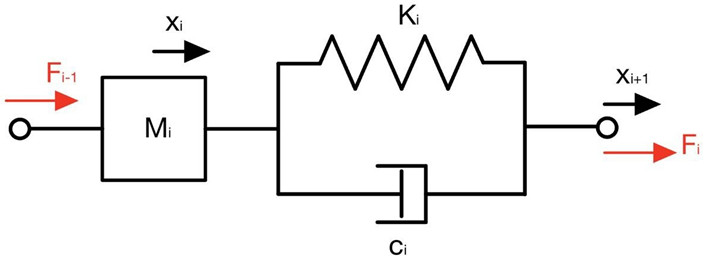
Finora, non si è fatto nessun riferimento alla massa del nastro, infatti i modelli precedenti erano relativi alla sola proprietà viscoelastica. È però consigliabile tenere in considerazione gli effetti inerziali della massa del nastro, per cui si può affiancare all’elemento visto prima una massa concentrata (mi), riferita ad un punto del generico tratto di nastro i-esimo, come mostrato in Figura 5.
Tale modello è una sorta di “elemento finito” con il quale è possibile modellizzare un tratto di nastro con proprietà identiche. È altresì possibile affiancare più elementi finiti di questo tipo ogni volta che si riscontrino differenti proprietà di rigidezza, smorzamento o massa (del nastro ovvero del materiale trasportato dal nastro stesso). L’equazione matematica differenziale dell’elemento finito di nastro è la seguente:

Coppia di attrito al perno
Nel caso di funzionamento a regime del sistema, è opportuno prendere in considerazione due fonti principali di attrito: l’attrito Coulombiano e l’attrito viscoso. Il primo non ha alcuna dipendenza dalla velocità ma solo dalla forza normale che si scambiano i due corpi in contatto. Il secondo è invece legato alle proprietà fisiche del lubrificante utilizzato, e produce una variazione del corrispondente coefficiente in base alle proprietà fisiche del lubrificante stesso come la viscosità. Il secondo contributo di dissipazione è quindi funzione anche della velocità di scorrimento fra i corpi.
Nel caso di modelli che debbano simulare fenomeni di transitorio, come ad esempio avvio, arresto o in generale condizioni di passaggio dalla condizione statica a una dinamica (o viceversa), entrano in gioco anche effetti di attrito a bassissime velocità. Si parla in questo caso di “effetto Stribeck”, il quale osservò sperimentalmente che, partendo da una condizione di attrito statico, il coefficiente progressivamente diminuisce fino al valore dell’attrito di Coulomb per basse velocità di scorrimento. L’unione dei tre fenomeni descritti, ovvero viscoso, Coulombiano e Stribeck, è chiamato attrito di Stribeck.
Modello per i transitori di funzionamento
Un modello che sia in grado di descrivere la dinamica di un impianto deve essere costruito attorno al componente principale, ovvero il nastro. E’ opportuno quindi rappresentare correttamente la complessità di questo componente, in particolare dal punto di vista dinamico. A tal fine è molto efficace l’approccio basato sul metodo degli elementi finiti impostato prima. Tutti gli altri componenti come tamburi e rulli possono essere considerati come fonte di sollecitazioni addizionali al nastro stesso, attraverso i punti di contatto; essi contribuiscono ad accrescere localmente l’inerzia del sistema. L’interazione tra nastro e tamburo può essere descritta in maniera semplificata considerando uno scambio diretto di forze tra i due componenti.
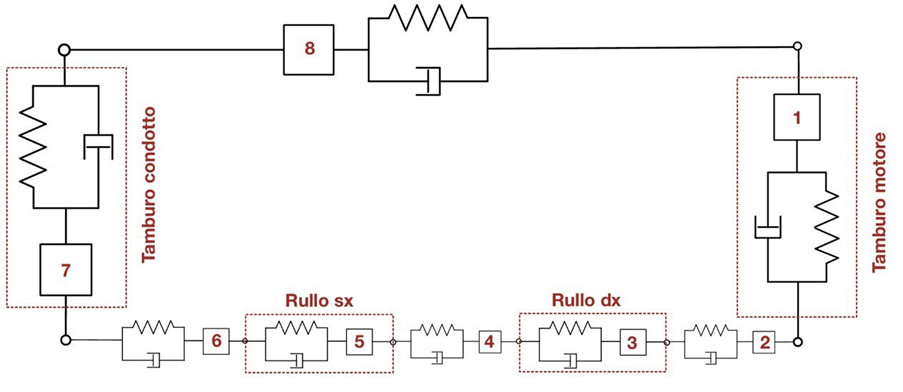
Un esempio di modello dinamico del sistema complessivo è riportato in Figura 6. Come si vede, in questo caso si è scelto di utilizzare otto elementi finiti per la modellazione del nastro, ciascuno comprendente un valore specifico di massa, smorzamento e rigidezza, distribuiti nel seguente modo:
- un elemento per ogni tratto di nastro a contatto con tamburi e rulli (elemento 1, elemento 3, elemento 5, elemento 7);
- un elemento per ogni tratto di nastro libero compreso tra i componenti rotativi (elemento 2, elemento 4, elemento 6, elemento 8).
La numerazione degli elementi parte dal tamburo motore e procede in senso antiorario fino al numero 8, corrispondente al tratto di nastro compreso tra i due tamburi.
I modelli matematici
Il modello matematico utilizzato per gli elementi non è esattamente il medesimo per tutti. Per gli elementi di nastro liberi, ovvero non a contatto con altri elementi, l’equazione di base è quella riportata in precedenza (Eq. 4). Invece, per gli elementi di nastro a contatto con tamburo e rulli, si considera un contributo di sollecitazione aggiuntivo causato dalla forza scambiata (Fsc) tra i due componenti. L’equazione in questi casi diventa:

Come visto in precedenza, le forze agenti sul nastro dipendono dalle proprietà reologiche del materiale di cui è costituito e dalle dimensioni del tratto di nastro a cui esse si fa riferimento. L’equazione di base per il calcolo di questa forza è:

Una volta scelti il numero di elementi finiti in cui suddivide il nastro, si può passare al calcolo dei parametri mi, ci e ki. Il primo dato da calcolare è la lunghezza a riposo (L0,i) di ogni tratto di nastro i- esimo. Una volta sottoposto al carico di tensionamento, la deformazione del nastro si può considerare in prima approssimazione costante in ogni tratto. I parametri di rigidezza e smorzamento possono essere calcolati come:

In cui ρlin è la densità lineare del nastro, En è il modulo elastico in direzione assiale del nastro e An è la sezione resistente del nastro.
L’ultimo step, che conclude la definizione del modello dinamico, consiste nella definizione delle condizioni iniziali. Queste corrispondono all’istante in cui il sistema è già stato pre-caricato e ha raggiunto una condizione di equilibrio. Una possibile definizione delle condizioni iniziali consiste nell’utilizzare un sistema di riferimento ortogonale alla sezione trasversale del nastro e nel fissare lo zero in corrispondenza della posizione iniziale della massa dell’elemento 1, ovvero quello a contatto con il tamburo motore.
Fonti
[1] CEMA. Belt conveyors for bulk materials. Conveyor Equipment Manufacturers Association, 1966. [2] Gabriel Lodewijks. «Two decades dynamics of belt conveyor systems». In: Bulk Solids Handling 22.2 (2002), pp. 124–132. [3] Iman Satria e Meifal Rusli. «A comparison of effective tension calculation for design Belt conveyor between CEMA and DIN Standard». In: MATEC Web of Conferences. Vol. 166. EDP Sciences. 2018, p. 01007. [4] Kevin T Andrews, Meir Shillor e S Wright. «On the dynamic vibrations of an elastic beam in frictional contact with a rigid obstacle». In: Journal of elasticity 42 (1996), pp. 1–30. [5] Piotr Bortnowski, Lech Gładysiewicz, Robert Król e Maksymilian Ozdo- ba. «Models of Transverse Vibration in Conveyor Belt—Investigation and Analysis». In: Energies 14.14 (2021), p. 4153. [6] TC Firbank. «Mechanics of the belt drive». In: International Journal of Mechanical Sciences 12.12 (1970), pp. 1053–1063.




