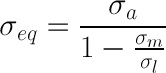di Francesco Chichi
Nell’articolo introduttivo pubblicato sul numero precedente abbiamo visto cosa siano le tensioni residue (tensioni presenti all’interno di un corpo in condizioni di equilibrio termico e meccanico), e come la loro categorizzazione più significativa sia quella che prende in considerazione la “lunghezza caratteristica” , ossia la dimensione spaziale entro cui lo stato tensionale interno si sviluppa e si equilibra.
In base a questo criterio si hanno:
- Tensioni residue del primo tipo: sono quelle che si sviluppano su scala macroscopica, tanto da poter essere analizzate utilizzando i tradizionali modelli continui, ossia senza tenere in considerazione le caratteristiche cristalline o multifasi del materiale
- Tensioni residue del secondo tipo : sono quelle collegate a stati tensionali generati da fenomeni di interfaccia o da disomogeneità fisica o metallurgica tra grandi adiacenti (es coesistenza di fasi nell’acciaio, orientamenti casuali di grani a comportamento anisotropo, ecc)
- Tensioni residue del terzo tipo: sono le tensioni residue la cui lunghezza caratteristica e’ inferiore alla dimensione del grano. Sono quindi stati tensionali generati da disomogeneità interne al grano (es dislocazioni, vacanze, imperfezioni del reticolo, ecc) e che si equilibrano all’interno di esso.
Piu’ in generale possiamo dire che le tensioni residue del III e del II tipo vengono accomunate nella definizione di “micro tensioni residue”, mentre quelle del I tipo vengono indicate come “macro tensioni residue” . Dopo aver visto cosa sono, non ci resta che capire quale impatto possano avere queste tensioni residue sul comportamento di un componente, e in che modo queste tensioni si vengano a creare all’interno di un corpo. Iniziamo quindi nell’affrontare il problema di come le tensioni residue influenzino il comportamento meccanico di un materiale.
Gli effetti delle tensioni residue
In termini generali si ha che dal punto di vista dell’interazione con le altre tensioni presenti, le tensioni residue devono essere trattate come ogni altra forma di tensione statica presente all’interno del corpo, e considerate in combinazione con tutte le altre tensioni presenti. Questo concetto si applica sia in senso microscopico , ossia quando si tratta di determinare l’effetto cumulativo delle tensioni residue del I, del II e del III tipo per dare la tensione residua complessiva, sia in senso macroscopico, ossia quando deve essere calcolato l’interazione delle tensioni residue con le altre tensioni statiche e/o dinamiche presenti sul componente. Ovviamente nella combinazione delle tensioni residue con le altre tensioni applicate è necessario ricordarsi come non necessariamente i sistemi di tensioni residue e applicate hanno gli stessi assi principali, per cui diventa fondamentale trasformare le tensioni residue nel sistema di assi principali delle tensioni applicate. Nel caso di uno stato di sollecitazione piano , detto
Q = angolo relativo formato tra il sistema di riferimento delle tensioni applicate e delle tensioni residue
sx , sy, txy = componenti dello stato tensionale residuo nel sistema di riferimento delle tensioni residue
sx’ , sy’, tx’y’ = componenti dello stato tensionale residuo nel sistema di riferimento delle tensioni applicate
Si ha che
v\:* {behavior:url(#default#VML);}
o\:* {behavior:url(#default#VML);}
w\:* {behavior:url(#default#VML);}
.shape {behavior:url(#default#VML);}
A questo punto, dopo aver convertito le tensioni residue nel sistema di riferimento principale delle tensioni applicate, e’ quindi possibile quantificare direttamente il contributo delle tensioni residue allo stato di sollecitazione complessiva del componente, utilizzando un qualsiasi criterio di resistenza .
Utilizzando ad esempio il criterio della energia di distorsione, indicando con
![]() le componenti della tensione applicata secondo gli assi principali
le componenti della tensione applicata secondo gli assi principali
![]() le componenti della tensione residua secondo gli assi principali
le componenti della tensione residua secondo gli assi principali
![]() la componente tangenziale della tensione applicata
la componente tangenziale della tensione applicata
![]() la componente tangenziale della tensione residua
la componente tangenziale della tensione residua
Si ha che la tensione complessivamente equivalente risulta
Abbiamo così definito quale sia il “peso” delle tensioni residue sulla resistenza meccanica di un componente .
Dall’equazione precedente è facile riconoscere come la presenza di tensioni residue abbia effetti migliorativi o peggiorativi sulle caratteristiche di resistenza di un componente , a seconda della natura trattiva o compressiva che esse assumono.
Considerazioni particolari devono essere fatte quando si devono considerare unicamente gli effetti di tensioni residue integranulari (II° tipo), come ad esempio quando si volesse prendere in considerazione effetti come la “stress corrosion” integranulare : in questo caso infatti la stessa natura microscopica delle tensioni residue e la loro orientazione “random” conseguente all’orientamento dei grani renderebbe privo di significato un approccio analitico come quello appena illustrato.
In questo caso l’esperienza insegna come l’approccio più valido sia quello di considerare il “worst case” costituito dalla coassialità della massima tensione residua con l’asse principale delle tensioni applicati, una condizione statisticamente presente con sicurezza e corrispondente alla più probabile condizione di innesco del fenomeno.
Chiusa questa “parentesi”, ritorniamo al caso più generale in cui le tensioni residue abbiano comunque una risultante macroscopica.
In termini di caratteristiche statiche (carico di rottura e/o snervamento), in pratica solo nel caso dei materiali fragili è possibile riconoscere un effetto diretto delle tensioni residue in essi presenti a riposo.
Probabilmente l’esempio più famoso (o perlomeno quello con cui tutti noi più spesso abbiamo a che fare) e’ costituito dal vetro temprato.
In questo materiale un rapido raffreddamento che investa la superficie esterna causa su questa superficie uno stato tensionale compressivo dell’ordine dei 100MPa ,a cui ovviamente deve corrispondere uno stato tensionale complessivamente equivalente nella parte più interna del materiale.
Tuttavia, visto che la profondità della zona temprata è indicativamente 1/20 dello spessore complessivo, ne risulta che comunque lo stato tensionale trattivo e’ trascurabile in senso assoluto (pochi MPa) .
I materiali con un comportamento plastico non riescono invece a beneficiare di questo tipo di miglioramento in termini di carico di rottura ( o di snervamento) , in quanto l’approssimarsi della condizione di plasticizzazione in esercizio porta comunque ad un “riazzeramento” degli stati tensionali interni.
Completamente diverso il discorso per quanto riguarda il comportamento a fatica, dove invece gli effetti delle tensioni residue non sono mai trascurabili, tutt’altro….
Le esperienze sperimentali dimostrano senza ombra di dubbio come l’influenza degli stati tensionali residui dipenda non tanto dal tipo di materiale da dal profilo di utilizzo del componente che con quel materiale è realizzato: l’influenza degli stati tensionali residui è massima quando il profilo di servizio del componente prevede un alto numero di cicli di ampiezza ridotta, mentre diventi progressivamente minore quanto più il profilo di servizio preveda cicli ad alta deformazione.
Anche in questo caso la giustificazione risiede nel fatto che in quest’ultimo caso sono sempre più presenti zone di deformazione plastica che tendono ad annullare o comunque a rendere inefficaci le tensioni residue presenti nel componente.
Stante la loro natura statica, il modo più semplice per tenerle in considerazione e’ ricorrere all’utilizzo di modelli tradizionali come quelli di Goodman, Gerber o Haigh.
Un efficace rappresentazione di quanto accade può essere fatta utilizzando un diagramma di Haigh, ossia un diagramma che, prendendo come riferimento la durata a fatica, riporti l’effetto della tensione statica sull’ampiezza della tensione alternata.
In altri termini, supposto che in assenza di una componente di sollecitazione statica la sollecitazione alternata che garantisca una vita utile infinita ( o di N cicli) abbia ampiezza sf , il diagramma di Haigh permette di calcolare quale sia l’ampiezza sf’ della sollecitazione alternata che, in presenza di una sollecitazione statica di ampiezza sm , permetta la stessa vita utile.
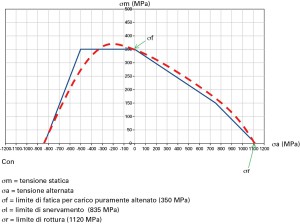
Facendo riferimento al diagramma di Haigh della curva limite di fatica per un acciaio da cementazione 16 CrNi4 riportata in figura 2, è facile osservare come
Tensioni residue di tipo trattivo comportino sempre una significativo peggioramento del limite di fatica
Tensioni residue di tipo compressivo comportino un medio miglioramento del limite di fatica per bassi valori delle stesse, mentre per valori piu’ elevati l’effetto sia comunque peggiorativo
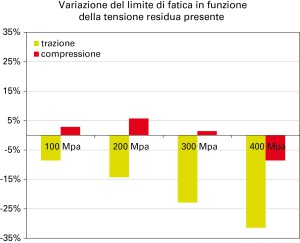
Nella figura 3 e’ riportata una quantificazione numerica di tale effetto per valori via via crescenti di tensioni residue trattive e compressive via via crescenti.
In termini generali, nel caso di tensioni residue trattive e’ possibile definire approssimativamente la tensione alternata pura equivalente alla combinazione della tensione alternata e della tensione statica effettivamente presenti ricorrendo all’espressione numerica dei criteri indicati in apertura di paragrafo, come ad esempio Goodman (eq 5) per materiali fragili e Sodenberg ( eq 6) per materiali duttili.
Dove
om = tensione statica effettivamente presente
oa= tensione alternata effettivamente presente
oeq= tensione puramente alternata equivalente alla combinazione di tensione statica e alternata effettivamente presenti
ol= limite di snervamento
or= limite di rottura
In questo approccio, delle tensioni residue si viene a tenere in considerazione soprattutto l’effetto macroscopico: in realtà le tensioni residue hanno un peso altrettanto importante anche nella determinazione dei diversi parametri correttivi che vengono introdotti nel passaggio tra il materiale ed il componente (sensibilità all’intaglio, fattori di forma, fattore di concentrazione delle tensioni, ecc)
Tuttavia per questi parametri non sono ancora disponibili modelli generalizzati come quelli appena descritti, ed in fase progettuale è necessario ricorrere a modelli numerici specifici per i diversi materiali, geometrie e condizioni di utilizzo.
Come nascono le tensioni residue
Adesso che abbiamo illustrato sul perché una progettazione “non conservativa” non possa fare a meno di tenere in considerazione le tensioni residue in un componente, l’aspetto da affrontare diventa quello di comprendere quali siano i meccanismi attraverso cui si generano le tensioni residue all’interno di un componente , e quali ne siano le cause.
Secondo una sintetica definizione spesso ripresa in molte pubblicazioni , le tensioni residue nascono da una “disomogeneità” delle caratteristiche meccaniche o metallurgiche di zone adiacenti all’interno di uno stesso materiale.
Questa disomogeneità può essere in termini di coefficiente di espansione termica, modulo elastico , limite di snervamento od altro, e può essere presente al momento della misura oppure essere una “memoria” dei trattamenti precedentemente ricevuti dal componente.
L’origine di queste “disomogeneità” possono essere ricondotte a 4 tipi di causa, molto spesso tra interagenti all’interno dello stesso processo:
– Termica
– Meccanica (deformazione plastica)
– Chimica
– Metallurgica (transizione di fase)
Tensioni residue termicamente indotte
I meccanismi attraverso cui si vengono a creare tensioni residue per via termica sono essenzialmente due:
– per variazioni di temperatura in materiali multifasici le cui fasi abbiano coefficienti di espansione termica distinti;
– per processi di raffreddamento non omogenei che portano a deformazioni differenziali tra le diverse zone dello stesso componente.
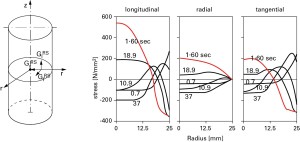
In rosso la condizone all’equilibrio termico finale (dati rielaborati a partire dalla pubblicazione “introduction to residual stress” di E. Macherauch)
Quest’ultima è una delle principali cause di nascita di tensioni residue all’interno di componenti massivi, con relativa rottura di numerosi componenti durante il rafffreddamento.
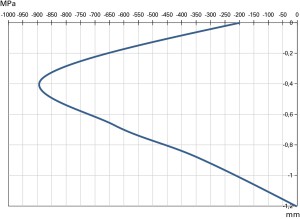
Tanto per dare un idea dell’ordine di grandezza delle tensioni residue indotte da processi di raffreddamento non omogenei, in fig. 4 è riportato l’andamento delle tensioni residue rilevate all’interno di un piccolo cilindro acciaio (lunghezza 150mm e diametro 50mm) raffreddato da 600°c a 0 con tempra in acqua : anche in assenza di tensioni applicate, in termini di energia di distorsione (eq la sollecitazione equivalente supera i 600 MPa!
Tensioni residue indotte da cause meccaniche
Anche nel caso delle tensioni residue indotte da cause meccaniche è possibile individuare due tipologie di causa
Le lavorazioni meccaniche per asportazione;
Le lavorazioni meccaniche per deformazione plastica.
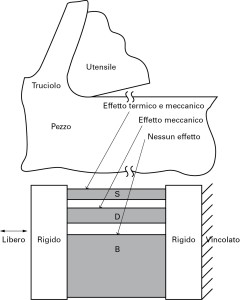
La natura fortemente localizzata della lavorazione meccanica per asportazione di truciolo permette di considerare il resto del componente come un vincolo rigido esterno
Relativamente alle lavorazioni meccaniche per asportazione, in realtà non è possibile pensare di tenere in considerazione solo il meccanismo puro e semplice dell’asportazione meccanica, in quanto in questa lavorazione i meccanismi che portano alla formazione delle tensioni residue sono molteplici.
Tra i diversi modelli , quello che attualmente viene ritenuto il più soddisfacente e’ il cosiddetto “modello termodinamico di Morrow” (fig 5) che vede nell’utensile una sorgente di sollecitazione elastica, plastica e termica, via via decrescente in funzione della profondità
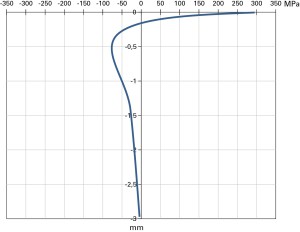
Conformemente a questo modello, in fig. 6 e’ riportato un tipico andamento delle tensioni residue in funzione della profondità
Generalizzare l’entità delle tensioni residue indotte dalle lavorazioni per asportazione è praticamente impossibile, stante la molteplicità dei parametri d lavorazione personalizzabili (velocità angolare dell’utensile, verso di rotazione, profondità della passata, velocità dell’avanzamento, ecc….)
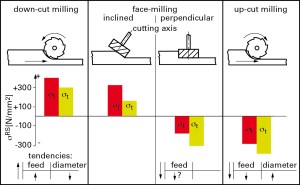
A titoli indicativo , nella figura 7 sono riportati l’andamento delle tensioni residue secondo i due assi principali per diverse impostazioni di lavorazione: e’ facile vedere come si possano ottenere indifferentemente tensioni residue trattive o compressive semplicemente combinando la direzione di rotazione dell’utensile e la direzione di avanzamento.
Relativamente alle lavorazioni per deformazione plastica, nel caso di trafilatura, estrusione e laminazione l’intensità delle tensioni residue diventa funzione di un “parametro di forma” D , costituito dal rapporto tra la sezione del materiale e la sua superficie di contatto con l’elemento deformante (bocca di estrusione , trafila o rulli di laminazione).
Per valori di D pari o inferiori a 1 (ossia forti rapporti di riduzione ) la deformazione risulta omogenea nella sezione, con conseguente omogenietà anche delle deformazioni plastiche e quindi assenza di tensioni residue
Aumentando il valore di D questa omogeneità viene persa e nascono le tensioni residue, che generalmente risultano di trazione sulla superficie e di compressione al cuore.
Ulteriori aumenti del valore di D (ossia per bassissimi rapporti di riduzione ottenuti operando su ampie sezioni di materiale, con deformazioni che non arrivano al cuore del grezzo ) possono far arrivare all’inversione del profilo delle tensioni, ottenendo uno stato compressione sulla parte esterna (lavorazione “skin pass”, migliorativa delle caratteristiche del prodotto)
Nel caso di queste tipologie di lavorazione è particolarmente pericoloso il caso di distribuzione delle tensioni residue asimmetriche rispetto all’asse di simmetria del prodotto finito (es per trafilatura con cilindri a diversa velocità o diverso diametro): in questo caso anche piccole asportazioni di materiale da una delle superfici possono comportare fenomeni di distorsione geometrica.
Tensioni residue indotte da reazioni chimiche
In questo caso le tensioni residue possono essere indotte da cambiamenti di volume conseguenti a reazioni chimiche , precipitazioni o trasformazione di seconde fasi.
Tra i processi espressamente utilizzati per la loro capacità di generare tensioni residue compressive si possono indicare la cementazione e la carbonitrurazione (fig 8).
Tensioni residue da transizione di fase
Ogni qualvolta una trasformazione di fase implica una variazione nella struttura cristallina del materiale, questo comporta variazioni volumiche dei singoli grani, che all’interno di un contesto piu’ o meno rigidamente vincolato porta alla nascita di tensionamenti elasto-plastici nel materiale.
Tale effetto è ancora più accentuato nel caso di leghe multifasiche , nelle quali oltre alla variazione di volume intrinseca dei singoli grani si devono anche gestire la differenza di variazione di volume tra le diverse fasi.
Ricordiamo che i meccanismi attraverso cui si arriva ad un cambiamento di fase possono sostanzialmente ricondotti a due modelli:
– Diffusivo (o distorsivo)
– Ricostruttivo
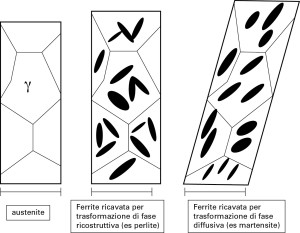
Esemplificazione delle variazioni geometrico-dimensionalisubite da una struttura policristallina di ferro-che subisca una trasformazione ricostruttiva o diffusiva
Nel caso di trasformazioni diffusive , ossia quelle in cui la trasformazione avviene per spostamento coordinato a breve raggio di singoli atomi, la struttura cristallina finale risulta dalla deformazione ordinata della struttura cristallina iniziale. In questo caso la variazione di volume indotta risulta anisotropa e prevede la presenza di un piano “invariante” (habit plane) e di una variazione dimensionale perpendicolare a tale piano. (incidentalmente, e’ questo il caso tipico delle strutture martensitiche, dove sono proprio le tensioni residue intergranulari a giustificare le elevate caratteristiche meccaniche dei materiali aventi questa struttura).
Nel caso di trasformazioni ricostruttive , ossia quelle in cui l’intera massa degli atomi subisce una diffusione casuale , la struttura cristallina finale risulta non correlata con quella iniziale. In questo caso la variazione volumica risulta isotropa . Nel caso degli acciai questa e’ la struttura tipoca della ferrite presente nell’austenite residua.
È quindi facile comprendere come in una lega bifasica costituita da grani aventi diversa struttura successivamente al raffreddamento siano presenti forti stati tensionali interni: caso tipico sono gli acciai ad elevato tenore di austenite residua.
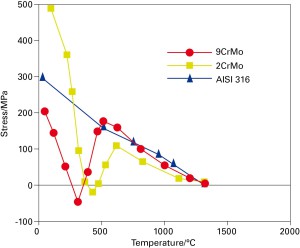
AISI 316 non subisce trasformazioni di fase
2CrMo subisce una trasformazione bainitica
9CrMo subisce una trasformazione martensitica
Mentre per l’AISI 316 si osserva un andamento lineare, che conferma la natura puramente termica delle tensioni residue che si instaurano nel materiale, per gli altri due acciai al di sotto dei 700°C si evidenziano gli effetti delle transizioni di fase
Un interessante esempio di come le transizioni di fase e la presenza di sistemi multifase comportino la nascita di tensioni residue , si possono confrontare le tensioni residue presenti in 3 diverse leghe di acciaio al variare della temperatura, così come riportate nella figura 10.
Mentre per l’AISI 316 si osserva un andamento lineare, che conferma la natura puramente termica delle tensioni residue che si instaurano nel materiale, per gli altri due acciai al di sotto dei 700°C si evidenziano gli effetti delle transizioni di fase.
Conclusioni
Le tensioni residue nascono dalla presenza all’interno di materiale di “disomogeneità” , o dalla memoria di disomogeneità presenti nel corso delle lavorazioni precedenti e poi bloccate durante le successive trasformazioni.
Tali disomogeneità possono riguardare tutte le caratteristiche meccaniche o metallurgiche di un materiale, e in pratica ogni passaggio meccanico, metallurgico, chimico o termico agisce da innesco per le tensioni residue: facile comprendere come ogni manufatto industriale ne sia affetto, in maniera maggiore o minore.
In termini quantitativi le tensioni residue possono raggiungere anche i limiti di rottura o di snervamento di un materiale, e anche se solitamente rimangono confinate in pochi mm di profondità , le tensioni residue sono quindi in grado di influenzare pesantemente le caratteristiche di resistenza di un materiale, soprattutto dal punto della resistenza a fatica.