La grande semplicità delle interfacce dei software di simulazione integrati nei CAD e la rapidità con cui vengono svolti i calcoli porta spesso il progettista a dare per scontato che, nel momento in cui si imposta una condizione al contorno, il software abbia implicitamente interpretato in maniera corretta il comportamento che lui vorrebbe dare al modello, e che così otterrà dalla simulazione esattamente i risultati che si aspetta. Nonostante che l’evoluzione delle interfacce dei software di calcolo abbia automatizzato e reso estremamente semplice l’impostazione di un’analisi, il progettista è tenuto a svolgere dei controlli, documentandosi sul funzionamento delle condizioni al contorno utilizzabili nel proprio software in modo per poter effettuare delle scelte consapevoli e coerenti. A differenza dei calcoli manuali, le simulazioni operano su modelli tridimensionali in cui i gradi di libertà dei corpi sono 6, e dove possono esserci più carichi applicati contemporaneamente con diverse direzioni nello spazio. In queste condizioni, anche facendo scelte apparentemente ponderate, non è semplice essere certi a priori di aver eseguito una impostazione corretta del calcolo e quindi si suggerisce di svolgere dei controlli a posteriori valutando attentamente i risultati ottenuti:
– Se precedentemente è stata fatta una prova di collaudo sulla struttura è possibile capire molto facilmente se le condizioni al contorno che si sono inserite siano corrette confrontando l’entità delle frecce e la deformata con i dati sperimentali
– Se si sta effettuando una simulazione su un progetto nuovo si suggerisce di raccogliere delle informazioni dai risultati per ottenere delle utili indicazioni sulla correttezza del calcolo: valutare attentamente se la deformata è verosimile, controllare se le reazioni vincolari coincidono col carico totale che si pensa di aver applicato alla struttura sommato al peso proprio, valutare se l’entità delle frecce e la zona dove è localizzato il loro valore massimo sono verosimili, identificare le zone dove le sollecitazioni sono più alte per capire se corrispondono alle zone dove, in base alla propria esperienza di progettazione la struttura è più plausibile che entri in crisi.
– Se si hanno dei dubbi sul funzionamento di una condizione al contorno (es. un carico o un vincolo), costruire un modello semplificato verificabile con calcoli manuali: eventuali differenze tra i risultati della simulazione e quelli del calcolo manuale indicheranno che sarà senz’altro da rivedere la propria scelta su una delle condizioni applicate.
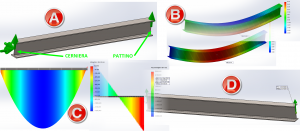
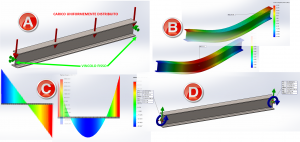
La figura 1 illustra un esempio pratico di una trave IPE, in cui una scelta sui vincoli fatta istintivamente e non supportata dai riscontri riportati sopra, possa portare ad ottenere dei risultati non corretti. La figura 2 mostra invece come si possano ottenere i risultati attesi modificando opportunamente le condizioni di vincolo.
Un’altra applicazione molto comune del calcolo strutturale è la determinazione della freccia massima di una vasca contenente un liquido (ad esempio una vasca per galvanica, fig. 3). In questo caso è importante conoscere in anticipo il comportamento della struttura per guidare la scelta sugli spessori delle lamiere, le sezioni dei profili di rinforzo che verranno utilizzati, il loro numero ottimale e la loro distribuzione. La difficoltà principale nell’impostare un calcolo di questo tipo è come applicare correttamente il carico per simulare l’azione del fluido sulle pareti. E’ necessario infatti tenere conto che il liquido esercita una azione di tipo idrostatico, con una pressione che cresce linearmente dal pelo libero al fondo della vasca.
In genere i software di calcolo strutturale hanno la possibilità di definire delle pressioni non uniformemente distribuite descrivendole con una equazione polinomiale rispetto ad un sistema di coordinate di riferimento.
Per descrivere la pressione idrostatica è sufficiente quindi costruire nel modello CAD un sistema di coordinate di riferimento con l’origine sul pelo libero, e fare in modo che l’asse y abbia la direzione della gravità (verso il basso) e verso positivo nella direzione in cui si aumenta la pressione (verso il fondo del serbatoio). Il valore di pressione da utilizzare, espresso in unità del SI (cioè N/m2) sarà il prodotto della densità del liquido per l’accelerazione di gravità. Poiché la pressione idrostatica è descritta da una relazione di tipo lineare in cui la pressione aumenta con la quota di altezza della vasca (y), i coefficienti dell’equazione avranno tutti valore zero, tranne C, che sarà pari ad 1.
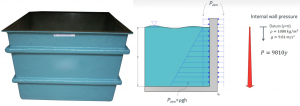
In figura 3 viene mostrata una schematizzazione delle condizioni di carico e dell’equazione che descrive il carico di pressione non uniforme. L’utente quindi deve costruire sul modello CAD un sistema di coordinate in corrispondenza del pelo libero con l’asse y rivolto verso il basso e poi applicare il carico di pressione variabile.
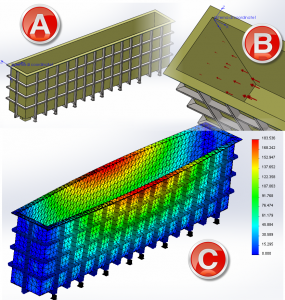
La figura 4 mostra la distribuzione dello spostamento nella vasca e l’andamento della deformata che forniscono già un riscontro positivo che la condizione impostata sia corretta: volendo effettuare una ulteriore verifica si suggerisce di controllare se le reazioni vincolari siano pari alla somma del peso totale del battente di liquido più il peso proprio della struttura.





