La fluidodinamica computazionale (CFD) rappresenta uno strumento essenziale per l’analisi dei sistemi complessi in numerosi settori, dall’ingegneria industriale a quella aerospaziale. Tuttavia, la simulazione della geometria completa, comprensiva di tutti i componenti, risulta spesso proibitiva in termini di costi computazionali. Questo articolo esplora un approccio ibrido in cui componenti complessi – quali filtri, pompe e ugelli – vengono semplificati mediante formule analitiche o analisi ridotte, mantenendo una affidabilità elevata e garantendo un livello di dettaglio comparabile a quello della simulazione completa.
di Carlo Augusto Pasquinucci
Introduzione
La fluidodinamica computazionale (CFD) si è affermata come una disciplina imprescindibile per l’analisi e la progettazione di sistemi che coinvolgono flussi di fluidi. Applicazioni pratiche spaziano dall’ingegneria aerospaziale, dove la simulazione del flusso attorno a strutture complesse è critica per la progettazione degli aerei, fino ai processi industriali, dove il controllo della circolazione dei fluidi è fondamentale per l’efficienza dei sistemi di produzione.
Nonostante i progressi tecnologici e l’incremento delle capacità computazionali, la simulazione della geometria completa di un sistema – con l’inclusione di ogni componente fisico – può risultare eccessivamente onerosa. In particolare, componenti la cui geometria o comportamento può essere predeterminato, come filtri, pompe o ugelli, costituiscono un nodo critico nel bilanciamento tra accuratezza della simulazione e risorse computazionali disponibili.
Questo articolo propone una strategia di semplificazione dei componenti complessi, che tramite modelli analitici o analisi ridotte, permette di integrare tali elementi in simulazioni CFD complete, riducendo il carico computazionale senza sacrificare l’accuratezza dei risultati. Nei paragrafi seguenti, verranno analizzati i fondamenti della CFD, le tecniche di semplificazione e alcuni esempi applicativi, evidenziando i vantaggi e le limitazioni di questo approccio ibrido.
Introduzione alla fluidodinamica computazionale
Alla base della CFD vi sono le equazioni di Navier-Stokes, che descrivono il comportamento dei fluidi in moto. Queste equazioni, unite alle leggi di conservazione della massa e dell’energia, forniscono un quadro matematico completo per la simulazione dei flussi:
- Equazione di continuità: garantisce la conservazione della massa.
- Equazione di quantità di moto: descrive il bilancio delle forze agente sul fluido.
- Equazione di energia: consente di monitorare lo scambio termico e le variazioni di energia.
La risoluzione numerica di tali equazioni richiede la discretizzazione dello spazio utilizzando delle celle volumetriche. Tuttavia, geometrie particolarmente grandi e complesse richiedono un grande numero di celle. Perciò, spesso, si rende necessario sviluppare metodologie che possano ridurre la complessità computazionale senza compromettere l’accuratezza dei risultati.
In particolare, nel caso di grandi geometrie contenenti diversi componenti, si cerca di semplificare il comportamento del flusso all’interno di essi, o attraverso dei modelli di complessità ridotta o direttamente con formule analitiche.
Analisi a parametri concentrati
Lo scopo di questo metodo è quello di sostituire la geometria di un componente con un metodo che permetta comunque di descrive la sua influenza sul moto del fluido e le sue caratteristiche.
In effetti, ci sono diversi componenti che presentano comportamenti che possono essere stimati a priori. Filtri, pompe e ugelli, ad esempio, operano in regime relativamente stabile e rispondono a leggi fisiche ben note. Questi elementi, se analizzati in dettaglio, potrebbero richiedere una mesh molto fine, ma la loro influenza principale sul fluido può essere descritta mediante:
- Formule analitiche: curve caratteristiche o informazioni fornite dal costruttore
- Modelli ridotti: utilizzando correlazioni empiriche integrano le proprietà principali del componente.
Una delle tecniche più utilizzate nei solver CFD è quella di introdurre un termine di perdita di carico nell’equazione della quantità di moto. Questo viene fatto aggiungendo un termine sorgente nella direzione del flusso.
Un altro metodo consiste nel correggere direttamente la pressione nelle celle adiacenti alla zona in cui è presente la perdita di carico. Il solver impone una riduzione della pressione tra due celle consecutive secondo l’equazione analitica del componente. Nel caso in cui si sostituisca a una pompa il suo effetto principale sul fluido e quindi l’aumenta di pressione nelle celle a valla di essa si compie un’approssimazione che in molti casi è in linea con le approssimazioni generali della simulazione. Stessa cosa può essere fatta con un filtro. Le celle a valle di questo componente avranno una pressione ridotta in funzione della legge di filtraggio, in base quindi alla velocità in ingresso.
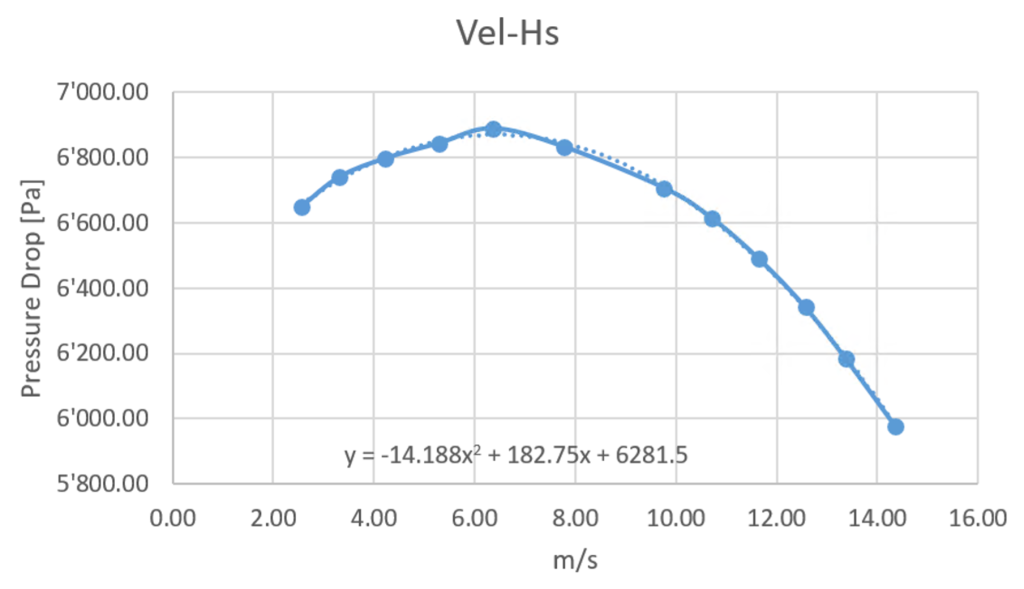
L’uso di formule analitiche per approssimare componenti in simulazioni CFD è spesso ostacolato dalla difficoltà nel reperire dati affidabili direttamente dai costruttori: molti produttori considerano le curve caratteristiche di pompe, filtri e ugelli come informazioni riservate. Per questo, non sempre forniscono tutte le informazioni, spesso poi solo tramite grafici e quindi non sempre facilmente fruibili. Spesso poi, le curva caratteristiche non sono facilmente approssimabili con equazioni di primo o secondo grado, creando quindi un ulteriore errore.
Analisi Monodimensionale (1D)
L’analisi monodimensionale considera il flusso come funzione di una sola coordinata spaziale, assumendo trascurabili le variazioni nelle altre due direzioni. In pratica, il comportamento del fluido viene descritto attraverso grandezze medie di sezione (come pressione, velocità e temperatura) lungo la direzione principale del flusso. Questo approccio risulta particolarmente efficace per lo studio di tubazioni e condotti, dove si vogliono prevedere perdite di carico e distribuzioni di portata senza risolvere il dettaglio tridimensionale del campo di moto.
Applicazioni tipiche includono:
Circuiti idraulici e pneumatici: in cui le equazioni di continuità, quantità di moto ed energia vengono risolte lungo il percorso del fluido per valutare pressioni, portate e comportamenti dinamici.
- Condotti e tubazioni: in cui si utilizza l’equazione di Darcy-Weisbach o correlazioni analoghe per stimare le perdite di carico.
- Scambiatori di calore: trattati con equazioni differenziali lungo la direzione principale del flusso, consentendo di valutare il trasferimento termico senza una modellazione completa in 3D.
Inoltre, l’analisi 1D può integrare componenti a parametri concentrati, utili per rappresentare in modo semplice elementi complessi (ad esempio pompe, valvole o serbatoi) senza la necessità di dettagli geometrici. Il vantaggio principale di questo metodo è la riduzione del numero di equazioni da risolvere, che consente di eseguire simulazioni più rapide ed efficienti. D’altro canto, l’approccio monodimensionale non cattura fenomeni trasversali o tridimensionali (come vortici e separazioni di flusso), il che ne limita l’applicabilità ai casi in cui tali effetti non siano significativi.
Analisi Bidimensionale (2D)
Nell’analisi CFD bidimensionale, il campo di moto del fluido è rappresentato su un piano, considerando soltanto due coordinate spaziali e trascurando le variazioni nella terza direzione. Questo approccio risulta particolarmente vantaggioso quando la geometria o le condizioni al contorno suggeriscono che le variazioni in una direzione siano trascurabili o poco rilevanti, come per esempio, problemi assialsimetrici. Sebbene semplifichi il problema rispetto a una modellazione tridimensionale, l’analisi 2D permette comunque di ottenere risultati significativi in termini di distribuzione di pressione, velocità e scambio termico.
Applicazioni comuni:
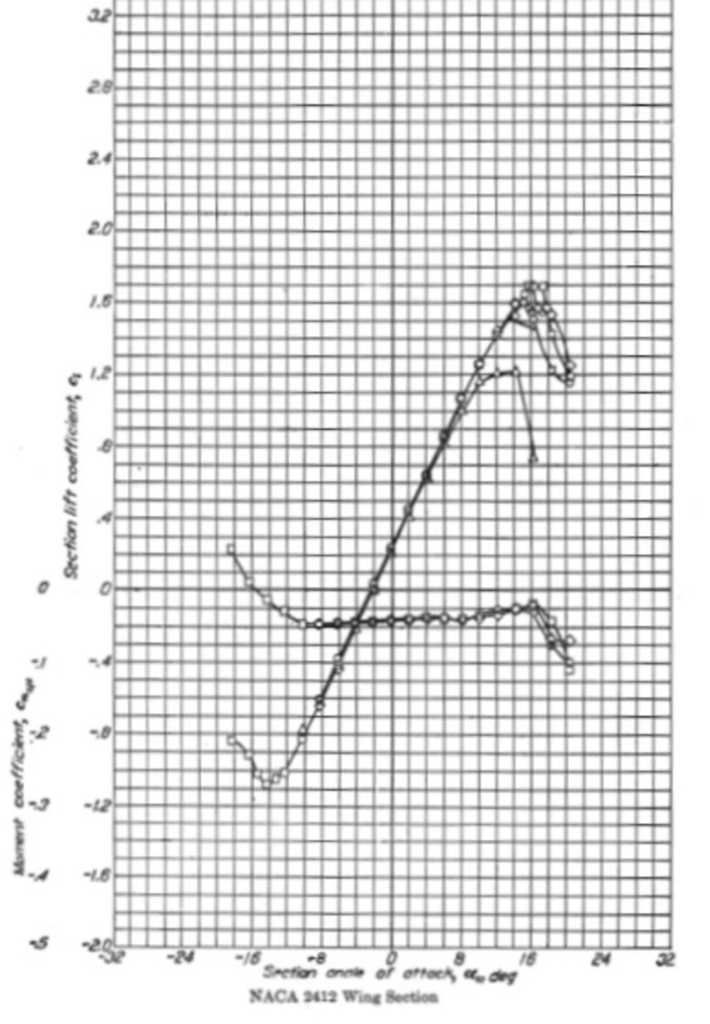
- Profili alari e superfici sommerse: in aerodinamica e idrodinamica, si studiano le sezioni di ali o di scafi in 2D per valutare portanza, resistenza e fenomeni di separazione dello strato limite, trascurando ovviamente la resistenza indotta e gli effetti di bordo.
- Ugelli e diffusori: i condotti convergenti-divergenti sono analizzati su una sezione piana per valutare il campo di pressione e velocità. Essendo spesso assialsimmetrici, questo comporta un errore minimo, in quanto ogni sezione avrà un comportamento identico.
- Scambiatori di calore a piastre: molti scambiatori industriali possono essere schematizzati in 2D, in particolare quelli a canali paralleli.
Le simulazioni 2D offrono quindi un buon compromesso tra accuratezza e costo computazionale, risultando ideali per studi preliminari, test di fattibilità e ottimizzazioni iniziali. In molti casi, dopo aver validato i risultati in 2D, si procede con un’eventuale analisi 3D per approfondire i fenomeni tridimensionali più complessi.
Un esempio applicativo
Per fare un esempio, è possibile simulare un ugello in tutti i 4 i modi:
Modello a parametri concentrati: in questo approccio, l’ugello viene rappresentato mediante modelli semplificati, basati su dati che il costruttore fornisce. Questi modelli catturano il comportamento complessivo dell’ugello attraverso una serie di equazioni che descrivono, in maniera globale, le proprietà come la portata e la perdita di carico, senza dover ricorrere a una rappresentazione dettagliata della geometria.
Analisi Monodimensionale (1D): qui il flusso viene considerato solo lungo la direzione principale, ovvero la coordinata longitudinale, assumendo che le variazioni nelle direzioni radiale e trasversale siano trascurabili. In questo modo, si calcolano le perdite di carico usando formule analitiche, riducendo significativamente il numero di equazioni da risolvere e semplificando il problema, pur ottenendo informazioni utili sul comportamento del flusso.
Simulazione Bidimensionale (2D): con questo metodo, si simula una sezione assialsimmetrica dell’ugello, ottenendo una rappresentazione più dettagliata del campo di pressione e della distribuzione della velocità lungo un piano. Pur non catturando l’intero comportamento tridimensionale, l’analisi 2D offre un buon compromesso tra dettaglio e costo computazionale, utile soprattutto in fase preliminare di valutazione.
Simulazione Tridimensionale (3D): infine, si può eseguire una simulazione completa che considera l’intera geometria dell’ugello. Questo approccio è il più esigente in termini di risorse computazionali, ma permette di analizzare con la massima precisione tutti i fenomeni complessi del flusso, inclusi effetti turbolenti e interazioni dettagliate con le pareti.
Svantaggi delle formulazioni semplificate
Le formulazioni analitiche, 1D e 2D comportano diverse semplificazioni numeriche oltre che geometriche.
In primo luogo, il flusso è orientato lungo la direzione principale e non ha quindi componenti trasversali. Questo implica che tutti gli effetti di swirl o comunque di rotazione del fluido vengo trascurati. Questa approssimazione può essere fonte di errore, in particolare all’uscita delle pompe o di valvole o ugelli che spesso vengono utilizzati apposta per creare questo effetto rotante e miscelare o nebulizzare meglio il fluido.
Un’altra approssimazione significativa riguarda la turbolenza e le perdite ad essa associata. In effetti, questo fenomeno è prettamente tridimensionale e quindi non catturabile attraverso simulazioni di ordine inferiore. All’uscita del componente semplificato, quindi, il flusso non avrà una turbolenza simile a quella reale.
Un altro problema riguarda il trattamento della variabile tempo, in particolare nelle simulazioni che includono componenti simulati a parametri concentrati. In effetti, trascurando o comunque approssimando le dimensioni dell’oggetto, il tempo di attraversamento dello stesso, ossia il tempo che ci metterebbe il fluido ad attraversarlo, risulta non correttamente calcolato.
Questo può avere un impatto significativo soprattutto nelle analisi transitorie, dove appunto si vogliono analizzare i cambiamenti del moto del fluido nel tempo.

Conclusioni e Prospettive Future
L’adozione di un approccio ibrido, che combina modelli semplificati per le componenti la cui dinamica può essere stimata in anticipo, rappresenta una strategia molto efficace per affrontare la simulazione CFD di sistemi complessi. Questo metodo, infatti, consente di sfruttare il meglio dei due mondi: da un lato si utilizzano modelli ridotti che permettono di ottenere risposte rapide, e dall’altro si integra una simulazione più dettagliata nei punti critici in cui è necessaria una maggiore accuratezza.
Uno dei vantaggi principali di questo approccio è la notevole riduzione dei tempi di calcolo. Grazie all’impiego di modelli semplificati, è possibile eseguire analisi in maniera molto più veloce, il che si traduce in iterazioni progettuali più efficienti e in una maggiore rapidità nell’ottenere risultati preliminari. Allo stesso tempo, non si sacrifica l’accuratezza: validazioni approfondite e accoppiamenti numerici ben definiti garantiscono che, nonostante la semplificazione, i modelli siano in grado di riprodurre fedelmente il comportamento reale del sistema.
Inoltre, questo approccio si presta a una vasta gamma di applicazioni, spaziando dall’ingegneria aerospaziale a quella industriale, e può essere adattato a molteplici settori tecnologici. La sua flessibilità lo rende uno strumento prezioso per chi deve affrontare problemi di fluidodinamica in contesti diversi e complessi.
Guardando al futuro, le prospettive di sviluppo sono molto interessanti. Ad esempio, la ricerca potrebbe concentrarsi sullo sviluppo di algoritmi di accoppiamento sempre più sofisticati, in grado di integrare in modo dinamico e armonioso domini semplificati e simulazioni dettagliate. Un ulteriore passo avanti potrebbe essere rappresentato dall’adozione di tecniche di machine learning, che permetterebbero di calibrare automaticamente i modelli semplificati basandosi sui dati in tempo reale, migliorandone così la precisione senza aumentare il carico computazionale.
Infine, c’è un grande potenziale nell’applicazione di questo approccio in scenari multi-fisici, dove la fluidodinamica si combina con altri fenomeni come la trasmissione del calore o le reazioni chimiche. In tali contesti, la capacità di integrare diverse discipline attraverso modelli ibridi può portare a soluzioni innovative e altamente efficienti.
In sintesi, questo lavoro apre la strada a una nuova generazione di simulazioni CFD, in cui una semplificazione mirata consente di coniugare efficienza e precisione. È una soluzione che risponde perfettamente alle esigenze di un mondo sempre più orientato verso soluzioni rapide, flessibili ed economicamente sostenibili.
Tabella 1 Analisi comparativa dei diversi metodi di analisi
| Livello di Analisi | Descrizione | Vantaggi | Svantaggi | Esempi di Applicazione |
| Parametri Concentrati | Il sistema è rappresentato da equazioni algebriche globali senza considerare distribuzioni spaziali di pressione, velocità o temperatura. | – Modelli semplici e veloci da risolvere – Basso costo computazionale – Facile implementazione in software di simulazione di rete | – Nessuna distribuzione spaziale delle variabili – Applicabile solo a sistemi altamente idealizzati | – Reti idrauliche e pneumatiche – Pompe e ventilatori modellati con curve caratteristiche – Perdite di carico concentrate in tubazioni |
| Analisi 1D | Il flusso è considerato funzione di una sola variabile spaziale (lungo un asse principale), trascurando variazioni trasversali. | – Buon compromesso tra accuratezza e velocità – Utile per circuiti idraulici e termici – Facile integrazione con modelli di rete | – Non cattura dettagli tridimensionali del flusso – Non adatto per geometrie complesse con vortici o separazioni | – Flusso in tubazioni e condotti – Scambiatori di calore a flusso controcorrente – Analisi preliminare di ugelli e venturi |
| Analisi 2D | Il flusso è modellato in un piano, considerando due dimensioni spaziali e trascurando le variazioni nella terza dimensione. | – Modello più dettagliato rispetto all’1D – Minore costo computazionale rispetto a un’analisi 3D – Utile per flussi in geometrie estese e sottili. | – Non rappresenta completamente effetti tridimensionali – Può introdurre errori nelle condizioni di bordo | – Flusso attorno a profili alari (aerodinamica) – Simulazione di ugelli in sezione – Flusso in canali aperti e scambiatori di calore a piastre |
| Analisi 3D | Il flusso è completamente tridimensionale, con tutte le equazioni di Navier-Stokes risolte nello spazio. | – Massima accuratezza e dettaglio – Cattura fenomeni complessi (turbolenza, separazione, vortici) – Essenziale per componenti con geometrie intricate | – Elevato costo computazionale – Richiede una mesh dettagliata e tempi di calcolo lunghi | – Simulazione di pompe e compressori – Flusso attraverso filtri con dettagli interni – Studi di aerodinamica e combustione |




