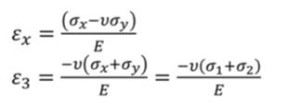Si definiscono “tensioni residue” tutte quelle tensioni presenti all’interno di un corpo in equilibrio meccanico e termico con il contesto che lo circonda. Si tratta quindi di tensioni che si equilibrano completamente all’interno del corpo, e che in pratica costituiscono un “residuo” della sequenza di trasformazioni meccaniche, chimiche e fisiche a cui il materiale di quel corpo e’ stato sottoposto. L’effetto delle tensioni residue su un componente prescinde dalla causa che le ha indotte, e la vera, unica discriminante tra le diverse tensioni residue è la dimensione spaziale su cui tale stato tensionale si sviluppa, dimensione spaziale che prende il nome di “Lunghezza caratteristica”.
Del resto, ogni tensione residua è inevitabilmente collegata ad una qualche forma di discontinuità all’interno del materiale, come ad esempio il diverso grado di plasticizzazione del cuore di un estruso rispetto alla sua parte superficiale, o il diverso comportamento in termini di espansione termica dei grani austenitici e martensitici in un acciaio, e cosi via: in pratica la “lunghezza caratteristica” di una tensione residua coincide con la dimensione spaziale entro cui si sviluppano le disomogeneità sopra esposte.
Limitando la nostra attenzione ai materiali metallici, si definiscono “macro” tensioni residue quelle in cui la lunghezza caratteristica e’ di ordine superiore a quella del grano, fino ad arrivare a coincidere con le dimensioni dell’interno componente. Si tratta quindi di tensioni il cui andamento si presenta comunque omogeneo su porzioni di materiale dimensionalmente significative, e la cui analisi puo’ essere svolta utilizzando i tradizionali modelli continui, ossia senza tenere in considerazione le caratteristiche cristalline o multifasi del materiale
Si parla invece di “micro” tensioni residue quando le tensioni residue sono generate da fenomeni di interfaccia o da disomogeneità fisica o metallurgica tra grandi adiacenti (es coesistenza di fasi nell’acciaio, orientamenti casuali di grani a comportamento anisotropo, ecc) , o addirittura sono dovute a disomogeneità interne al grano (es dislocazioni, vacanze, imperfezioni del reticolo, ecc).
In figura 1 è possibile osservare una sezione di un estruso di alluminio , in cui è facile riconoscere le differenze metallurgiche tra lo strato superficiale, quello intermedio e il cuore del materiale, differenzea cui ovviamente corrispondono stati tensionali variabili con la profondità
Le macro tensioni residue vengono solitamente prese in considerazione per determinare le prestazioni meccaniche complessive di un componente (come il carico di rottura o lo stato di danneggiamento), mentre le micro tensioni residue sono invece fondamentali per la verifica dello stato del materiale e della bontà di eventuali trattamenti meccanici, termici o metallurgici eseguiti sul materiale, anche se la loro presenza e’ in grado comunque di influire anche sulla prestazione complessiva del componente, almeno per quanto riguarda la fase di innesco di fenomeni puntuali (enucleazione della cricca da fatica, innesco di stress corrosion, ecc)
Anche se le tensioni residue sono un fenomeno cosi diffuso e concettualmente noto, non per questo possiamo dire che esse siano solitamente tenute in considerazione in forma esatta in sede di progettazione e di verifica, sopratutto per il fatto che esse sono difficilmente modellizzabili e quindi non predicibili per via analitica.
E’ quindi ovvio che la considerazione delle tensioni residue all’interno dello sviluppo progettuale o della verifica analitica non può prescindere dalla loro misurazione: del resto già un secolo e mezzo fa Lord Kelvin ci diceva che possiamo dire di conoscere solo ciò che sappiamo misurare….
La misura delle tensioni residue
Tralasciando tutte quelle tecniche che, per la loro complessità o costo , non hanno un reale utilizzo in ambito industriale, possiamo dire che in pratica le tecniche per il rilievo operativo delle tensioni residue si suddividono in due gruppi:
– Tecniche basate sul principio della diffrattometria
– Tecniche basate sull’utilizzo di sensori estensimetrici
Le prime sono tecniche assolutamente non distruttive , caratterizzate dal fatto di poter operare su volumi di materiale di poche centinaia di mm ^3, fatto che le rende ottimali per il rilievo delle micro tensioni residue superficiali
Le seconde sono invece tecniche basate su una (di solito minima) asportazione di materiale , asportazione che permette al materiale stesso un rilassamento rilevabile mediante una opportuna disposizione di estensimetri.
In considerazione del fatto che l’asportazione del materiale non può mai scendere sotto l’ordine del mm², e analogamente la superficie coperta da un estensimetro non è mai inferiore a qualche decina di mm², ne consegue che questa tecnica è invece applicabile al rilevamento delle macro tensioni residue.
Iniziamo quindi ad esporre le applicazioni delle misure delle micro tensioni residue mediante tecniche diffrattometriche.
Le misure diffrattometriche
Il principio fisico che sta alla base della misura delle tensioni residue è abbastanza semplice.
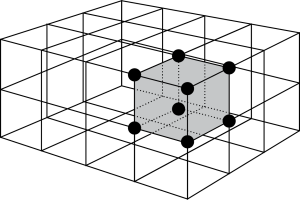
In ogni materiale con struttura cristallina (come lo sono tutti i metalli, ma non solo essi…) gli atomi occupano nello spazio posizioni che si ripetono con regolarità geometrica, dando luogo ad una struttura che può essere pensata come la ripetizione di un modulo base , modulo solitamente indicato come “cella elementare” : tale struttura prende il nome di “reticolo cristallino” (figura 2).
All’interno di un reticolo cristallino è sempre possibile individuare famiglie di piani paralleli tra loro su cui giacciano gli atomi del reticolo, e per i quali si definisce distanza interplanare “d” la distanza intercorrente tra due piani adiacenti appartenenti alla stessa famiglia.
Come ben illustrato nella figura 3, per ogni reticolo tali famiglie di piani possono essere molteplici, eventualmente ciascuna con una sua propria distanza interplanare “d”
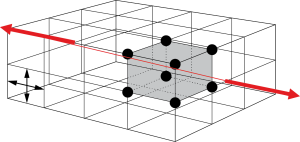
Nel caso in cui il materiale venga sottoposto ad una sollecitazione, esso subirà una deformazione coassiale alla direzione della sollecitazione conformemente alla legge di Hook, e una deformazione perpendicolare alla suddetta direzione secondo l’effetto Poisson (figura 4).
Poichè la distanza interplanare “d0” per un materiale non sollecitato e’ una grandezza che possiamo considerare nota a priori , è ovvio che dalla misura della distanza interplanare “d1 ” presente in un determinato momento è possibile risalire alla deformazione del materiale e quindi alla sollecitazione a cui è sottoposto .
Il problema diventa ora quello di misurare la distanza interplanare appena menzionata, ed è qui che entra in gioco la diffrattometria…..
La tecnica diffrattometrica prevede di colpire il materiale con un fascio di raggi X con una componente monocromatica dotata di energia sufficiente da poter interagire con gli atomi posizionati sui piani reticolari interni del materiale.
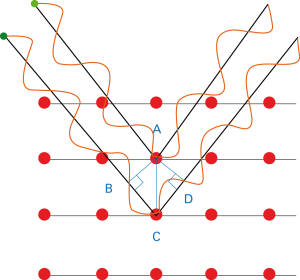
Come illustrato in figura 5, quando il fascio incidente colpisce il materiale esso e’ in grado di eccitare gli atomi appartenenti ai diversi piani reticolari , che a loro volta emettono una radiazione con lunghezza d’onda identica a quella della radiazione che li ha colpiti.
reticolari.
In base a semplici considerazioni trigonometriche, illustrate anche nella figura 6, e’ facile capire come le radiazioni emesse dagli atomi appartenenti a piani reticolari diversi risultino tra loro sfasate in maniera dipendente da:
l=lunghezza d’onda della radiazione
q=angolo di incidenza
d=distanza interplanare
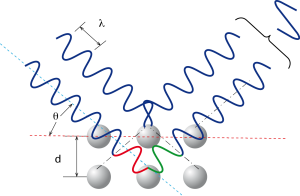
In particolare, come scoperto dai Braggs nel 1913 (che dalla scoperta guadagnarono, oltre all’onore di poter definire con il loro nome la suddetta legge, anche il premio Nobel) , data una radiazione di lunghezza d’onda nota l0, l’interferenza tra le radiazioni emesse dal materiale e’ costruttiva quando l’angolo di incidenza q risulta tale che
2*d*sin θ
————- = n
λ
Dove “n” rappresenta un numero intero.
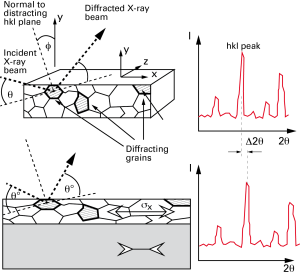
A questo punto, essendo nota la distanza interplanare dei diversi materiali in assenza di tensione interna e la frequenza del fascio diffratto, dal rilevamento della differenza dell’angolo di diffrazione reale rispetto a quello ideale è possibile quantificare lo stato tensionale interno presente (vedi figura 7)
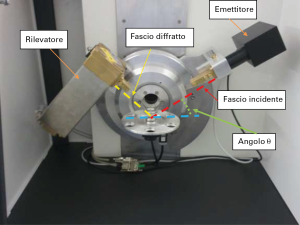
L’esecuzione pratica di questa misura è ben illustrata nella figura 8 , dove e’ rappresentato un diffrattometro fisso da laboratorio in cui i possono distinguere il generatore del fascio incidente e il rilevatore del fascio diffratto.
Generatore e rilevatore vengono fatti ruotare in maniera sincrona così da variare con continuità l’angolo q e riuscire ad individuarne l’ampiezza per cui risulti massima la radiazione diffratta: una volta determinato tale angolo, dalla legge di Braggs è immediato risalire alla distanza interplanare, da questa alla deformazione presente e da qui alla sollecitazione imposta.
Poiché ovviamente l’orientamento dei piani interni non necessariamente è allineato con la superficie esterna del componente, ne consegue che i valori misurati risulteranno orientati nello spazio con direzioni individuate come da convenzione in figura 9, dove “R” indica la perpendicolare alla superficie esterna.
In tale condizione la ricostruzione spaziale dello stato di sollecitazione e a partire dalla deformazione misurata s e’ ottenibile tramite le equazioni
v\:* {behavior:url(#default#VML);}
o\:* {behavior:url(#default#VML);}
w\:* {behavior:url(#default#VML);}
.shape {behavior:url(#default#VML);}
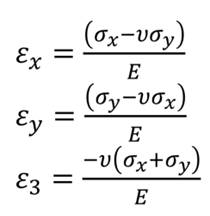Dove “n” indica il coefficiente di Poisson
Mentre la ricostruzione spaziale della sollecitazione è data dalla relazione
Dove
e “n” continua ad indicare il coefficiente di Poisson
Come è facilmente intuibile, le misure mediante tecniche diffrattometriche costituiscono un metodo assolutamente puntuale, in grado di analizzare volumi spaziali dell’ordine del centinaio di mm cubi, in quanto lo spot del fascio incidente ha un raggio inferiore al mm ed anche la profondità di penetrazione non supera i 10 – 30 mm a seconda del materiale analizzato.
Tale estrema risoluzione nel senso della profondità costituisce sicuramente un vantaggio in termini di capacità di discriminare le tensioni superficiali rispetto al cuore, ma anche una limitazione quando ci sia la necessità di svolgere analisi negli strati immediatamente sottostanti quelli superficiali.
Tale limite può essere superato asportando progressivamente lo strato superficiale mediante un aggressione elettrochimica controllata, esponendo via via gli strati interni del materiale senza indurre perturbazione negli stati tensionali, come avverrebbe con una asportazione meccanica.
L’uso operativo delle misure diffrattometriche
(per gentile concessione di 2Effe Engineering Srl).
Note nei loro principi basilari fin dalla metà del secolo scorso, le misure diffrattometriche ono diventate uno strumento industriale solo negli ultimi anni, prima grazie ad una serie di diffrattometri da laboratorio di semplice utilizzo, e successivamente grazie ad una nuova generazione di diffrattometri finalmente portatili, che hanno permesso di far uscire la tecnica dai laboratori per portarla sul campo.
Come già anticipato, il principale utilizzo delle informazioni in merito alle micro tensioni residue è per la verifica dello stato metallurgico di un materiale e della bontà di eventuali trattamenti meccanici, termici o metallurgici eseguiti su quel materiale.
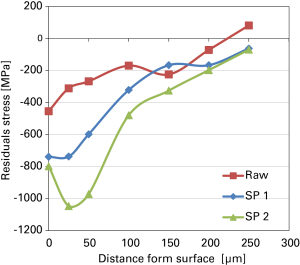
Senza ombra di dubbio possiamo dire che le misure diffrattometriche sono l’unico vero strumento di messa a punto e di controllo per i trattamenti di shot peening: come esempio, in figura 11 sono riportati gli andamenti delle tensioni residue in funzione della profondità prima su un ingranaggio “grezzo” e poi su ingranaggi analoghi sottoposti a trattamento di shot peening utilizzando due set up aventi la stessa intensità nominale (in almen).
È evidente come a due set up equivalenti in termini di energia complessiva di impatto ma diversi in termini velocità, flusso e tipologia di sfere finiscano per generare distribuzioni spaziali delle tensioni residue ben diversi: un informazione ricavabile solo attraverso le tensioni residue.
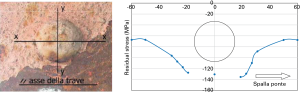
Ma la flessibilità operativa dei diffrattometri ha trovato applicazione anche in settori impensati, come ad esempio il restauro del Ponte Longo alla Giudecca, a Venezia.
Questo ponte, realizzato nel 1895 utilizzando piatti metallici e profili angolari uniti tra loro per chiodatura ribattuta a caldo, nel 2005 è stato sottoposto ad un completo restauro conservativo.
Proprio nell’ottica di svolgere un restauro massimamente conservativo, da parte della committenza venne deciso di procedere alla rimozione e sostituzione solo di quelle chiodature che avessero ormai perso il loro pensionamento.
Conclusioni
Essendo un fenomeno ancora troppo complesso da modellizzare, in pratica la conoscenza delle tensioni residue può passare solo attraverso la loro misura operativa.
Vista le enormi differenze che possono esistere in termini di lunghezza caratteristica, non esiste una tecnica di misura “universale” in grado di misurare indifferentemente le diverse tipologie di tensioni residue: nel caso delle micro tensioni residue misurazioni su volumi di materiale dell’ordine del centinaio di micron cubi possono essere eseguite mediante tecniche che sfruttano la diffrazione dei raggi X intepretata attraverso la legge di Braggs.
Mediante tale applicazione è possibile controllare lo stato metallurgico di un materiale e la bontà dei trattamenti termici e superficiali a cui è stato sottoposto: in tal senso particolarmente significativo è l’uso delle misure diffrattometriche per la messa a punto e il controllo di trattamenti di shot peening.
La realizzazione di una nuova generazione di diffrattometri portatili ha ulteriormente ampliato le possibilità operative con misure anche su impianti fissi o u su componenti comunque di dimensioni incompatibili con le misure di laboratorio (turbine Pelton, reattori chimici, ecc….).
