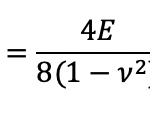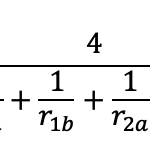Molti dei sistemi meccanici che ci circondano sono composti da più componenti aventi le più disparate forme. In molti casi poi, tali corpi interagiscono tra loro, si toccano e si caricano vicendevolmente. Come calcolare dunque lo stato tensionale di un corpo a contatto con un altro?

di Franco Concli

Sembra strano ma il contatto tra corpi è un aspetto molto importante e più diffuso di quanto si pensi nei sistemi meccanici. Esempi se ne trovano in moltissimi ambiti, dagli ingranaggi che fanno funzionare l’orologio da polso, ai cuscinetti del frullatore per non parlare del contatto ruota-binario del tram che molti di noi usano per recarsi al lavoro. C’è chi potrebbe obiettare che preferisce la macchina. Ed anche qui, tralasciando i cuscinetti delle ruote e gli ingranaggi del cambio, si hanno molti altri contatti, come ad esempio tra camme e punteria del motore.

Immaginando i corpi come infinitamente rigidi, il contatto avviene puntualmente o al più lungo una linea (in funzione della curvatura delle superfici a contatto). I copri reali però hanno una loro rigidezza finita e quindi si deformano. Il contatto si distribuirà pertanto su una superficie. Sempre rimanendo nel campo teorico, due sfere idali deformabili avranno un’area di contatto circolare, mentre due cilindri paralleli formeranno un’area di contatto rettangolare.

Il problema della distribuzione della pressione all’interno di tali aree è stato studiato in modo approfondito dal fisico tedesco Heinrich Hertz. La teoria formulata dallo scienziato si applica a materiali isotropi omogenei che operino in campo elastico, ipotizzando di avere superfici ideali con raggi di curvatura molto maggiori rispetto alle dimensioni delle superfici a contatto, trascurando di fatto l’effetto della rugosità e gli attriti.

Teoria del contatto sfera-sfera

Come accennato in precedenza, due sfere ideali a contatto aventi diametri d₁ e d₂ formeranno un’area di contatto circolare avente raggio pari ad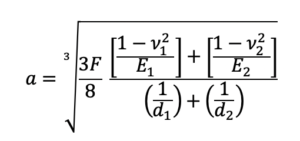

a viene detta semi-ampiezza del contatto. Il valore massimo della pressione si ha al centro dell’area di contatto ed assume un valore pari a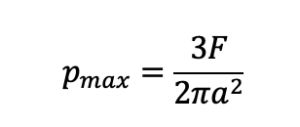

La presenza di uno stato tensionale multiassiale anche nel caso di un carico (F) monoassiale è dovuto al fatto che il materiale, compresso nella direzione di applicazione della forza tenda ad espandersi nelle altre due direzioni in cui è però presente altro materiale che ne contrasta la deformazione. Di fatto viene quindi a generarsi uno stato tensionale di compressione in cui tutte le tensioni principali sono negative.

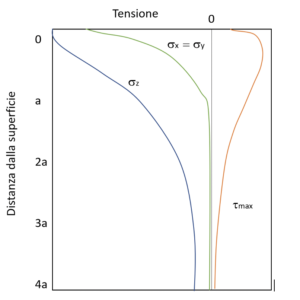
Figura 1 mostra l’andamento delle tensioni all’interno del materiale. La tensione normale di compressione  assume valore massimo assoluto in superficie e tende a decrescere allontanandosene. Il massimo dello sforzo di taglio  si ha al di sotto della superficie. Questo, come si vedrà nel seguito, sarà la principale causa di cedimento dei sistemi soggetti a contatto.

Teoria del contatto rullo-rullo

Analogamente a quanto visto per il contatto sfera-sfera, è possibile determinare la semi-ampiezza dell’area di contatto tra due rulli secondo la teoria di Hertz. L’area di contatto rettangolare avrà dimensioni  in cui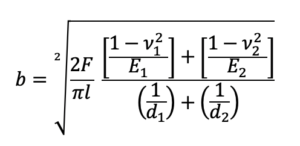

Anche in questo caso, l’andamento delle tensioni interne prevede un massimo della componente radiale in prossimità della superficie. Lo sforzo di taglio avrà un massimo in corrispondenza di una profondità pari a 0.75b.

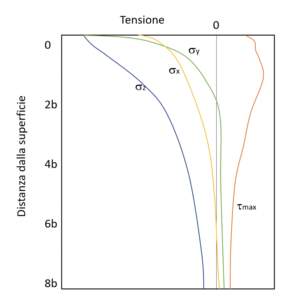
Cedimento per fatica da contatto

Come accennato precedentemente, è opinione comune che i cedimenti per fatica da contatto siano causati principalmente dalla presenza di uno sforzo di taglio  che, se presenta un andamento ciclico (questo lo si ha sia nelle ruote dentate che nei cuscinetti o nel contatto ruota rotaia), possa portare alla nucleazione e successiva propagazione di cricche sub-superficiali. La propagazione e unione di più cricche superficiali può portare al distacco di porzioni di materiale dalla superficie (cosiddetti pit). Innescato il fenomeno, si ha un repentino peggioramento dovuto al fatto che l’area effettiva di contatto risulta ridotta a causa delle zone danneggiate che non entrano più in contatto, facendo aumentare le pressioni Hertziane e le sollecitazioni. Inoltre, nel caso di contatto lubrificato, si ha un effetto di pompaggio per cui nella cricca penetra del lubrificante che al ciclo successivo la manda in pressione facendola propagare ancor più velocemente.

Figura 3 mostra un esempio di superficie danneggiata a pitting. Si riescono ad individuare in modo chiaro i punti di nucleazione delle cricche e le direzioni di propagazione.

Teoria del contatto fra corpi a doppia curvatura

Nei capitoli precedenti si sono trattati i casi di contatto tra sfere e tra rulli. Più in generale la teoria di Hertz è applicabile a superfici con curvatura generica. Per semplificare la trattazione successiva, d’ora in poi si assumerà che i corpi a contatto siano fatti dello stesso materiale per cui  e . Le due superfici a contatto potranno essere descritte ognuna dai due raggi di curvatura. Si avranno quindi  ed  per la prima superficie e  per  per la seconda.

I semiassi  e dell’area di contatto risulteranno pari a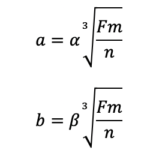

in cui

 

Esempio applicativo

Sebbene i cuscinetti volventi siano altamente standardizzati e difficilmente un progettista necessiti di calcolare la pressione effettiva nel contatto, sono un ottimo esempio per mostrare gli step di calcolo.

Si supponga di avere un cuscinetto con sfere di diametro  = 19.2 mm che rotolino su una pista con scanalatura avente raggio  pari a 9.98 mm. L’anello interno ha un raggio pari a  = 33.6 mm mentre quello esterno ha un raggio  = 52.8 mm. Il cuscinetto ha 12 sfere ed è caricato con una forza radiale  pari a 60000 N.

Il carico supportato dalla sfera più caricata è noto essere, in accordo alla formula di Stribeck pari a

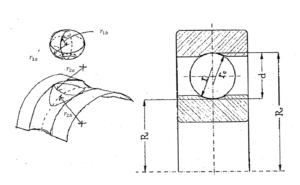
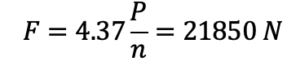
Con riferimento al contatto sfera – pista interna, si ha (per un acciaio)

Da tabella 1 si possono quindi ricavare  e  che risultano pari a 1.438 e 0.735 rispettivamente.

I semiassi dell’ellisse risulteranno quindi pari a  = 2.01 mm e  = 1.03 mm e la pressione di contatto 5039 MPa.

Conclusioni

 

I contatti sono un aspetto fondamentale in molti sistemi meccanici. La teoria di Hertz, seppur con delle approssimazioni, è uno strumento utile per calcolare le pressioni tra superfici a curvatura generica soggette a forze esterne ed in contatto tra loro.

Bibliografia

[1] Robert Errichello How to analyze gear failures, Journal of Failure Analysis and Prevention 2(6):8-16

[2] Giovanni Nerli, Costruzione di Macchine, Noccioli Editore