Analisi Statica FEM o il modo più semplice per analizzare una struttura

Come verificare qualsiasi situazione di carico in maniera semplice e rapida.

di Francesco Grispo

Introduzione

L’analisi statica FEM rappresenta un approccio fondamentale nell’ambito dell’ingegneria moderna, rivoluzionando il modo in cui si comprendono e progettano strutture e componenti soggetti a carichi statici.

Nel contesto di un’analisi statica, ci si concentra esclusivamente sulla condizione di equilibrio di un sistema, ignorando le variazioni nel tempo delle grandezze coinvolte. Questo include la considerazione di forze applicate, vincoli e proprietà dei materiali come costanti.

In questo articolo, verranno esplorati i principali aspetti da tenere in considerazione per condurre un’analisi statica mediante il Metodo degli Elementi Finiti e come massimizzarne l’utilità pratica. Inoltre, verrà utilizzato un esempio applicativo per illustrare concretamente l’applicazione di questa metodologia.

I 6 punti fondamentali dell’analisi statica

Si analizzano ora i 6 dati fondamentali necessari per un’analisi agli elementi finiti:

1. Geometria da Analizzare: La geometria in oggetto costituisce il focus primario dell’analisi. In genere, questa rappresenta una versione semplificata rispetto ai disegni di progettazione, e talvolta è possibile trascurare dettagli specifici.
2. Caratteristiche del Materiale: Il materiale svolge un ruolo fondamentale nella simulazione. In un’analisi statica, è essenziale disporre di informazioni riguardanti il modulo di Young, il coefficiente di Poisson, la densità, la tensione di snervamento, la tensione di rottura e la deformazione di rottura. Questi parametri permettono di creare un modello semplificato della risposta del materiale, noto come modello bilineare, che rappresenta un’analisi non lineare. Inoltre, la densità consente di considerare i carichi inerziali, come la gravità e le accelerazioni.
3. Generazione della Mesh: È fondamentale suddividere la geometria in piccoli elementi noti come “elementi finiti”. Questa discretizzazione finita è necessaria perché rappresenta un’approssimazione della geometria continua. Ciascun elemento finito è caratterizzato da una formulazione matematica specifica, che è essenziale per applicare i parametri appropriati. Ad esempio, per gli elementi di tipo piastra, è necessario tenere conto dello spessore, mentre per gli elementi trave occorre considerare area ed inerzia. Gli elementi di tipo molla richiedono l’utilizzo di costanti di elasticità, e così via.
4. Carichi e Vincoli: È essenziale avere una comprensione chiara delle forze che agiscono su un oggetto e dei vincoli che lo limitano. I carichi possono derivare dalla meccanica dell’oggetto in questione o da specifiche normative. I vincoli sono determinati dalla modalità di ancoraggio della struttura all’ambiente circostante.
5. Combinazione dei Diversi Carichi: I vari carichi e vincoli possono essere combinati in modi diversi. Ad esempio, se consideriamo un aereo in volo livellato e desideriamo valutare la resistenza dell’ala, comprendiamo che un singolo caso di carico coinvolge la forza di portanza sull’ala, il peso dell’aereo, la spinta del motore e il momento generato dal motore. Inoltre, è importante considerare le condizioni di vincolo dei longheroni all’ala. Un singolo “caso di carico” può quindi comprendere diversi carichi e vincoli.
6. Normative per il Post-Processing: I risultati di questa analisi tipicamente includono campi di stress, campi di spostamento e forze localizzate in punti specifici. Tuttavia, senza normative di riferimento, questi dati possono risultare privi di significato. È importante disporre di regole e normative che guidino l’interpretazione dei risultati e il confronto con i valori limite. Anche se una struttura può sopportare il carico fino al punto di snervamento, è buona pratica non progettare sistematicamente al limite di questo valore. Le normative forniscono indicazioni su quanto ci si possa discostare da tale limite senza sovradimensionare eccessivamente la struttura.

Se anche solo uno di questi punti è assente, non è possibile condurre un’analisi adeguata. Ad esempio, immaginate di non avere informazioni sul tipo di materiale da utilizzare. La scelta tra alluminio e polietilene per una struttura può avere un impatto significativo sulla sua prestazione. Allo stesso modo, se non si conoscono i fattori di sicurezza da applicare in base alle normative di riferimento, è impossibile stabilire se la struttura soddisfa i requisiti di accettabilità richiesti dall’ente di certificazione.

È importante ricordare la “regola d’oro” delle simulazioni: “inaccuratezza in ingresso, inaccuratezza in uscita”. Se i dati inseriti nell’analisi sono inesatti o inventati, i risultati ottenuti saranno altrettanto inaffidabili.

Pertanto, è fondamentale comprendere che l’analisi FEM non è una semplice operazione di “premere dei tasti e vedere che cosa accade”, come in un videogioco. Le decisioni basate su una simulazione hanno un impatto significativo sulle scelte progettuali e possono portare al fallimento di un progetto, con tutte le conseguenze che ne derivano.

Esempio applicativo dell’analisi FEM

Per una migliore comprensione del processo di analisi statica, si esamina un caso applicativo concreto. Si considera un piccolo UAV (Veicolo Aereo Non Pilotato) ad ala fissa. Si supponga pertanto che la struttura dell’UAV pesi circa 0,3 kg e che debba trasportare un payload di 1 kg.

Nel contesto di questa simulazione, l’obiettivo sarà valutare come la struttura dell’UAV reagirà ai carichi dovuti al peso proprio e al carico utile. Questo esempio pratico ci consentirà di applicare i principi dell’analisi statica in modo concreto e vedere come i risultati influenzeranno le decisioni di progettazione per garantire che il veicolo possa svolgere il suo compito in modo sicuro ed efficiente. Ipotizzando un volo livellato, si devono calcolare le forze da applicare alla struttura alare.

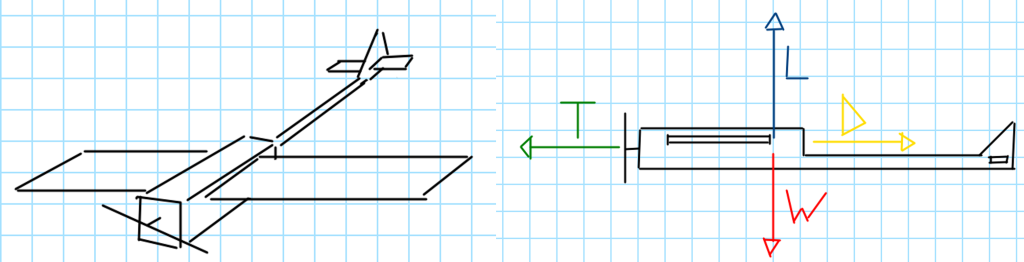
Per semplificare, si ipotizza che l’intera portanza sia generata dall’ala, anche se in realtà questa non rappresenta una condizione accurata, ma funziona bene come prima approssimazione. In fondo, si sta effettuando una fase di predimensionamento.

Dall’analisi del diagramma di corpo libero, si ottiene:

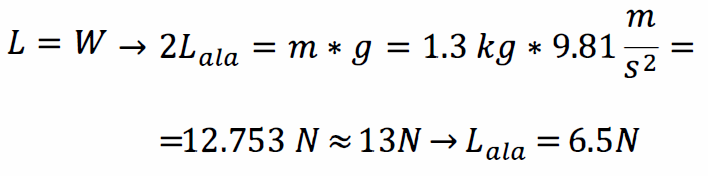
È possibile trascurare la forza di resistenza, poiché solitamente è molto più piccola. Un altro carico da considerare è il peso proprio dell’ala, al quale è necessario applicare l’accelerazione di gravità.

Materiale e geometria

Il materiale utilizzato per l’ala è una lega di alluminio 2024, con un modulo di Young di 70 GPa, un coefficiente di Poisson di 0.27 e una densità di 2700 kg/m³. Dai dati di bibliografia, risulta che il valore dello snervamento è di 290 MPa.

In figura è riportata la geometria semplificata della semiala soggetta all’analisi. Poiché la copertura non costituisce una componente strutturale, l’attenzione è rivolta esclusivamente alla resistenza della struttura portante. In questa fase di predimensionamento, non viene preso in considerazione il peso delle pannellature di copertura o di eventuali correntini. Le dimensioni della struttura sono, b_/2 = 0.450 m e c = 0.120. 

La struttura è modellata mediante elementi shell di tipo piastra, il che implica che lo spessore è unicamente un parametro numerico. Gli spessori delle centine e dei longheroni sono impostati a 1 mm.

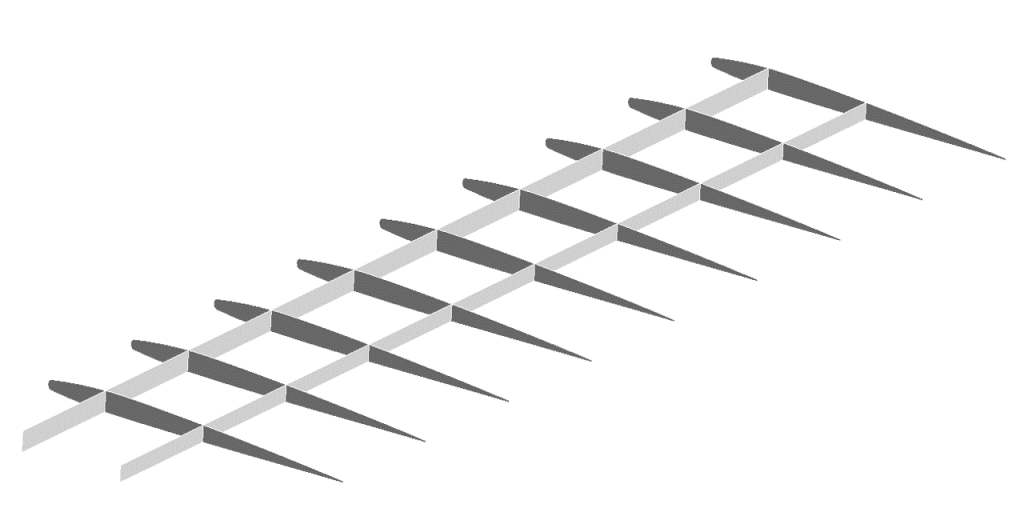
Il carico di portanza è applicato ai bordi esterni dell’ala, simulando il suo trasferimento dalla copertura direttamente alla struttura stessa. Inoltre, è applicata l’accelerazione di gravità verso il basso. La parte radicale dell’ala è soggetta a un vincolo di incastro, che blocca sia le traslazioni che le rotazioni.

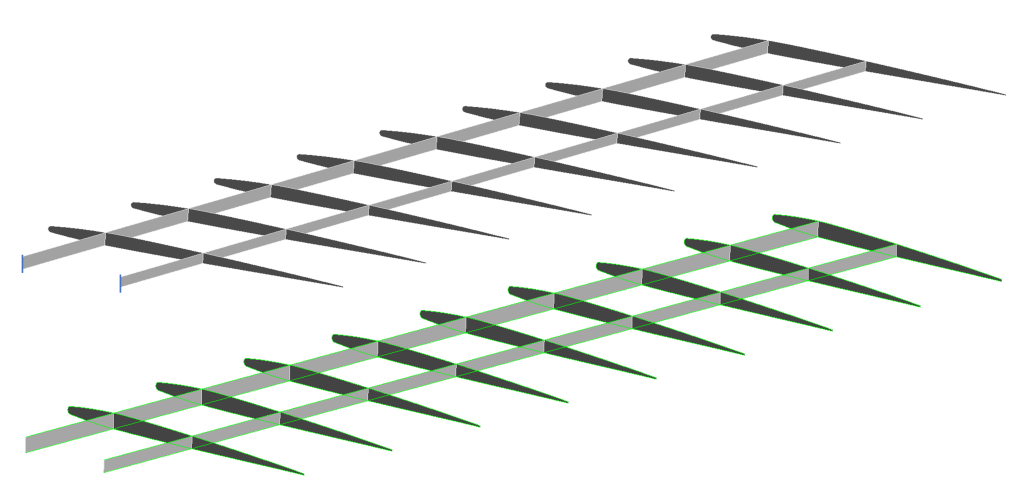
La geometria è stata discretizzata utilizzando elementi quadratici con dimensioni di 0,5 mm. Ciò ha generato una mesh molto densa poiché una griglia di calcolo più fitta fornisce risultati più precisi. Tuttavia, è importante notare che ciò comporta tempi di calcolo più lunghi e richiede una maggiore quantità di memoria.

Risultati

Alla conclusione dell’analisi, si ottengono i seguenti campi di spostamento e stress. Come limite massimo, si considera una deformata pari a L/20 mentre come riferimento per lo stress, si adotta il valore di snervamento ridotto di un fattore 1.5, seguendo il tipico coefficiente di sicurezza aeronautico.

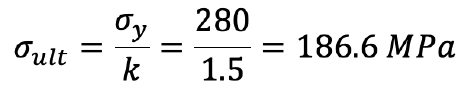
In tabella sono riportati i valori ottenuti:

	Valore ottenuto	Riferimento	MoS	Stato
Stress (MPa)	204 MPa	186.6 MPa	-0.08	No
Deformata (mm)	18 mm	22.5 mm	0.25	Ok

Si può ben intendere che la struttura non risulta verificata dal punto di vista degli stress

Una soluzione è quella di aumentare lo spessore dei longheroni da 1 a 3 mm, tenendo lo spessore delle centine a 1 mm.

Si ottengono i seguenti risultati:

	Valore ottenuto	Riferimento	MoS	Stato
Stress (MPa)	50.8 MPa	186.6 MPa	2.67	Ok
Deformata (mm)	4.3 mm	22.5 mm	4.23	Ok

Con questa nuova modifica la struttura risulta verificata e si può procedere allo step successivo della progettazione.

Conclusioni

Attraverso l’esempio applicativo precedentemente presentato, è stato possibile comprendere cosa comporti effettuare un’analisi FEM e quali parametri siano coinvolti, insieme alle possibili approssimazioni e all’interpretazione dei risultati.

Naturalmente, esistono molti altri concetti che richiedono spiegazione. Alcuni esempi includono:

1. La menzione di un’analisi lineare suggerisce l’esistenza di un’analisi non lineare. Quali sono le differenze?
2. Perché è stata scelta una semplificazione tramite elementi shell invece di una modellazione solida?
3. Cosa significa un “elemento quadratico” e quali tipi di elementi esistono?
4. In che modo la densità della mesh influisce sui risultati?
5. Se esiste un’analisi statica, esisterà anche un‘analisi dinamica? Come funziona?
6. Come si utilizzano efficacemente le condizioni di vincolo e reazione?

Queste rappresentano solo alcune delle domande che verranno affrontate e discusse nella rubrica CAE Academy.