In un progetto, lo snervamento non è l’unico caso possibile di rottura. È importante tenere conto anche della possibilità di collasso o di instabilità di buckling.
di Francesco Grispo
Per comprendere al meglio il fenomeno di instabilità di buckling viene presa in esame un’azione che tutti noi abbiamo fatto almeno una volta. Si considera uno stuzzicadenti tenuto tra pollice e indice. Quando si inizia a premere, lo stuzzicadenti si incurva fino a rompersi a metà.
Ma come mai, a fronte di un carico puramente compressivo, avviene una rottura che può essere ricondotta a flessione?
A differenza di quanto esposto dalla teoria, dove tutto è perfetto, nella realtà esistono le imperfezioni. Tali imperfezioni possono essere dovute al materiale (potrebbe essere che una parte è leggermente più densa o più rigida di un’altra) oppure dovute al modo con cui si applica il carico, che nella realtà presenterà sempre una piccola eccentricità rispetto al centro della sezione.
A fronte di questi difetti, da quello che doveva essere un profilo di stress a compressione, si ottiene un profilo di stress tipico della flessione (ossia asimmetrico), che porta l’oggetto a muoversi fuori dal piano di riferimento, rendendo critica una situazione di carico che in realtà non lo era.
Questo scostamento fuori dal piano, se il carico è eccessivo, può portare all’instaurarsi di un fenomeno di instabilità (il braccio generato dalla deformata genera un momento che a sua volta genera una deformata più elevata che a sua volta genera un momento e così via).
Ipotizziamo di analizzare una colonna tramite un modello a parametri concentrati. Si ipotizza di modellare la colonna come una trave incernierata con tutta la rigidezza flessionale concentrata alla cerniera.
Effettuando l’equilibrio dei momenti, si può scrivere:
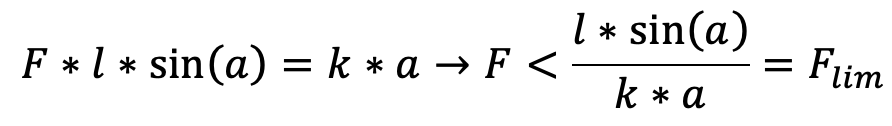
Si può vedere come, se il valore di forza supera il valore di forza limite, la struttura non è più in grado di resistere al carico.
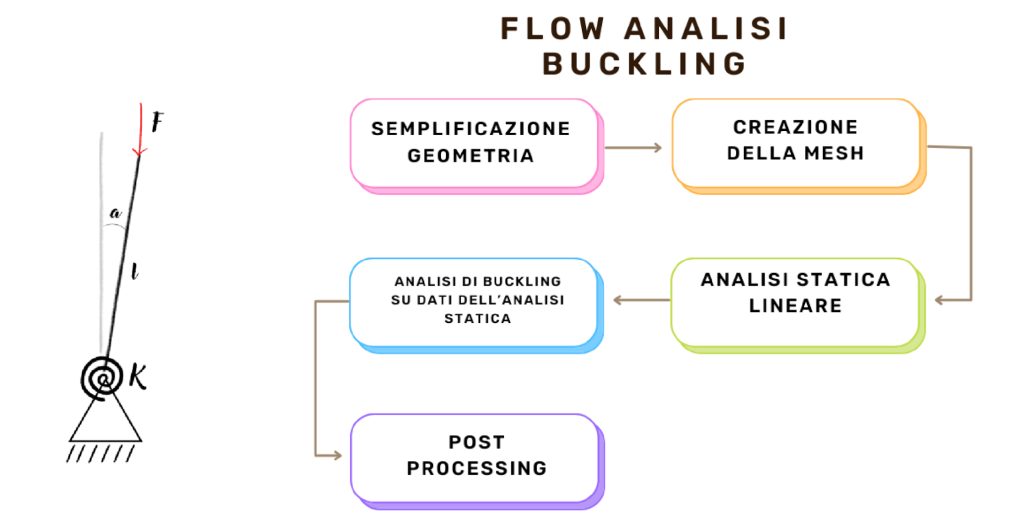
Come analizzare il buckling tramite il FEM?
Per simulare questo comportamento si utilizzano due strade:
- Approccio LBA (Linear Buckling Analysis, ndr);
- Approccio non lineare in cui ad ogni iterazione aggiorno utilizzo la configurazione deformata dell’iterazione precedente per calcolare la nuova matrice di rigidezza.
In questo articolo si andrà a studiare solamente la metodologia LBA, essendo l’approccio non lineare una tecnica molto avanzata che richiede la conoscenza e la padronanza delle metodologie non lineari.
La tecnica LBA prende in considerazione ha due scopi principali:
- Calcolare il carico critico;
- Indicare la deformata dovuta al carico critico.
Dal punto di vista teorico, queste grandezze prendono il nome rispettivamente di fattore di sicurezza e modo proprio di buckling.
Metodologia di risoluzione delle analisi di buckling
Per la metodologia di risoluzione, essa è simile all’analisi modale.
Questo è possibile perché dal punto di vista matematico, il problema di buckling lineare è simile al problema di analisi modale.
La differenza in questo caso sta nell’utilizzo delle matrici. Se nell’analisi modale le matrici utilizzate sono la matrice di massa e la matrice di rigidezza, in questo caso l’autoproblema da risolvere è:
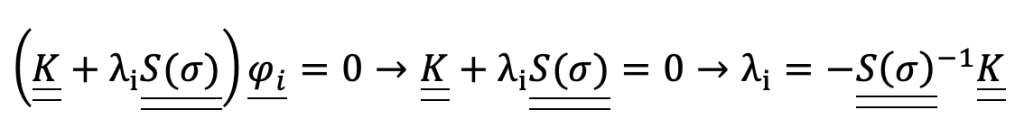
Dove compaiono la matrice di rigidezza e la matrice di rigidezza geometrica che è funzione del campo di stress a cui è sottoposto il materiale.
I simboli utilizzati hanno il seguente significato: K è la matrice di rigidezza, S è la matrice di rigidezza geometrica dipendente dagli sforzi, λ è il fattore di buckling, φ è la deformata modale.
Pertanto, il solutore impiegato altro non farà che risolvere l’inversione della matrice di rigidezza geometrica. Il problema vero deriva dal calcolo di questa matrice.
Essa è funzione del carico applicato e delle condizioni al contorno utilizzate e pertanto non si può effettuare un’analisi di Buckling senza effettuare un’analisi statica.
Così come l’analisi modale fornisce risultati a diversi valori di frequenza, così l’analisi LBA fornisce diversi valori di carico di buckling, ma bisogna analizzarli con attenzione:
- L’unico valore di interesse è il primo valore di “frequenza” di buckling, in quanto i valori successivi indicano un carico per cui già avvenuto il collasso della struttura.
- Se si dovesse ottenere un valore negativo, significa che il carico sarà critico se orientato in maniera opposta. La ricerca, perciò, dovrà sempre essere rivolta, in prima battuta, ai soli valori.
- I valori ottenuti tendono a essere sovrastimati rispetto al valore reale, il che permette di essere in sicurezza ma potrebbe portare ad un sovradimensionamento non necessario della struttura.
Guardando la deformata di buckling, essa sarà solamente qualitativa, non riuscendo a cogliere il vero verso in cui avverrà e non sarà in grado di dirci come si comporterà la struttura dopo il collasso.
Un esempio applicativo
Si analizza un caso reale di una struttura complessa, studiando una struttura di carpenteria sottoposta a peso proprio concentrato nella parte superiore dell’impalcato.
Si confrontano pertanto i risultati dell’analisi statica con i risultati derivanti dall’analisi di buckling.
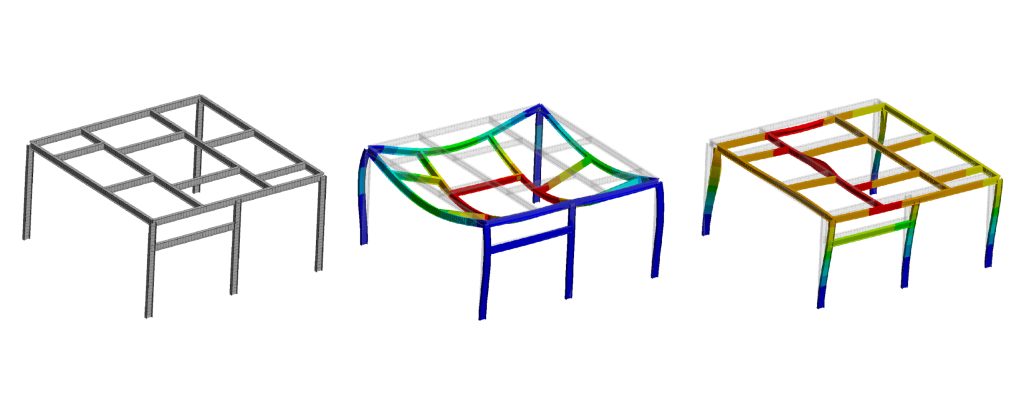
Il primo aspetto che si può cogliere è la diversa tipologia di deformata a cui si giunge. Nel caso dell’analisi statica si può notare come la deformata sia la classica freccia derivante dallo studio statico. Nel caso invece dell’analisi di buckling, si vede come la deformata ricordi quella di un’analisi modale, con la presenza di diverse onde e semionde. Inoltre, si può vedere come la struttura collassi lateralmente invece che centralmente, in quanto la parte meno rigida della struttura sono proprio le colonne.
Analizzando il valore di carico critico, in questo caso si è ottenuto un valore di 63. Questo numero sta a significare la seguente cosa:
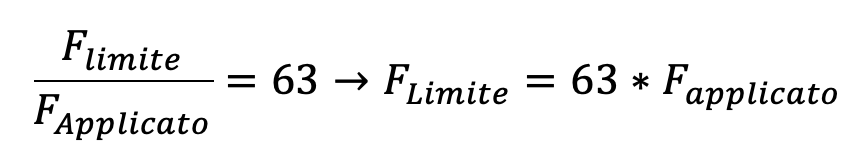
Significa che il numero trovato è effettivamente un fattore di sicurezza e che in questo caso la struttura è in grado di reggere 63 volte il carico prima di presentare instabilità di buckling (significa che si romperà prima a taglio).
Se invece il carico applicato fosse stato unitario, il valore trovato sarebbe stato effettivamente il carico di buckling:
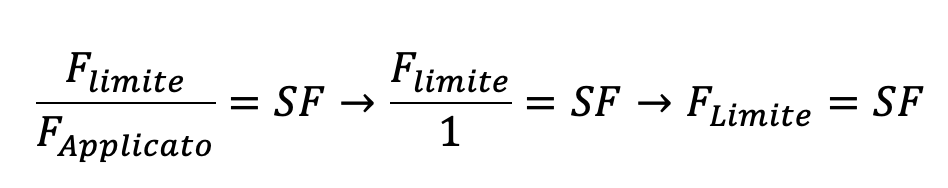
Da notare che i valori sono sempre uguali a coppie di 2 (o comunque molto simili). Questo deriva dal fatto che la deformata è qualitativa e perciò uno rappresenta il movimento in direzione positiva mentre l’altro il movimento con il vettore cambiato di segno.
Si deve infine tenere a mente che la LBA è utile per effettuare un dimensionamento preliminare della struttura e che il suo utilizzo non permette di conoscere il comportamento post collasso.
Questa tipologia di comportamento è studiabile tramite analisi non lineari, dove, passo dopo passo, si calcola la deformazione della struttura fino ad arrivare alla configurazione deformata finale.





