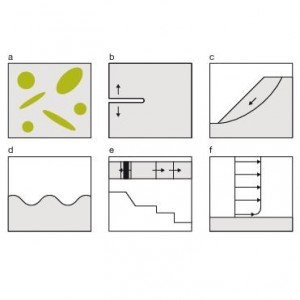
Ci sono molti problemi ingegneristici che presentano la necessità di modellare e risolvere discontinuità: è il caso delle cricche della meccanica della frattura, dell’interfaccia tra materiali differenti, dell’interazione fluido-struttura. In tutti questi casi la tradizionale modellazione ad elementi finiti presenta limiti e difficoltà. Tali problemi possono essere superati adottando il metodo XFEM, eXtended Finite Element Method.
Nel presente contesto industriale, caratterizzato dalla definizione di prodotti in grado di ridurre l’utilizzo dei materiali e garantire una maggiore efficienza energetica, è sempre più comune il dover fronteggiare situazioni una volta definite estreme e che sono divenute “di routine”, grazie alla possibilità di modellare molti problemi con il metodo degli elementi finiti.
In alcuni casi, tuttavia, l’applicazione degli elementi finiti presenta alcuni limiti, legati sia a problemi di modellazione (in quanto le geometrie da modellare sono complesse e danno luogo a mesh con elementi distorti con, conseguentemente, risultati meno accurati) sia a risultati poco accurati (in quanto le approssimazioni introdotte per modellare il campo delle grandezze che definisce il problema non sono in grado di garantire una loro adeguata rappresentazione). E’ questo il caso delle cosiddette discontinuità, situazioni comuni in molte applicazioni d’interesse tecnico. Un classico esempio di discontinuità sono le fessure o cricche, analizzabili con i concetti della Meccanica della Frattura, caratterizzate da una singolarità numerica e da un elevato gradiente degli sforzi attorno all’apice della cricca stessa. Tale singolarità non può essere colta dagli usuali elementi finiti e solo introducendo opportune distorsioni (con la tecnica del “1/4 point”) è possibile ritrovare un’adeguata descrizione del campo di spostamenti nella vicinanza dell’apice. Anche in questo caso, tuttavia, rimangono problemi di modellazione, in quanto, ad esempio, se si vuole seguire lo sviluppo della cricca è necessario rimodellare volta per volta l’elemento con la cricca e questo, soprattutto il tre dimensioni, può risultare poco agevole.
Altre situazioni che presentano discontinuità possono essere l’interfaccia tra materiali differenti (un tale caso si presenta, ad esempio, nelle strutture ibride), oppure nei problemi in cui è importante modellare l’interazione fluido-struttura. In tutti questi casi il metodo degli elementi finiti si basa su mesh attentamente definite con tecniche particolari che permettono di cogliere, in qualche modo la discontinuità, ma richiedono un onere di modellazione che può divenire importante.
L’XFEM (eXtended Finite Element Method)
Per ovviare a tali problematiche è possibile utilizzare un approccio di modellazione e calcolo numerico che riprende e modifica il FEM e permette la corretta modellazione delle discontinuità senza che queste siano introdotte nel mesh, non richiedendo, quindi, manipolazioni. Grazie a tali proprietà e alla sempre maggiore popolarità di problemi tecnici che includono l’analisi di questi aspetti, questo metodo, chiamato XFEM, è oggetto di sempre più numerose attenzioni in molti settori industriali ed è stato introdotto in alcuni software commerciali di simulazione a elementi finiti.
Il metodo XFEM (eXtended Finite Element Method), introdotto nel 1999 (T. Belytschko, T. Black, Elastic crack growth in finite elements with minimal remeshing, International Journal for Numerical Methods in Engineering, Volume 45, Issue 5, pages 601–620)
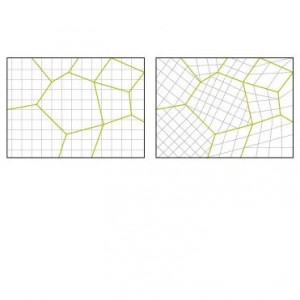
XFEM è caratterizzato da un arricchimento locale delle funzioni di forma del metodo degli elementi finiti, in modo tale da seguire correttamente l’andamento delle grandezze che governano la discontinuità proprio in prossimità di tale discontinuità. Il concetto alla base del metodo è, quindi, una migliore approssimazione del campo di spostamenti che è localmente modificato aggiungendo termini orientati alla soluzione di un problema specifico. Ad esempio, nel caso della modellazione di una cricca, viene introdotta la funzione di Heaviside (funzione e gradino) per arricchire i nodi che vengono attraversati dalla propagazione della cricca, mentre le funzioni analitiche che descrivono il campo di spostamenti in prossimità della della cricca vengono utilizzate per i nodi che definiscono l’apice della cricca.
Ma il vantaggio più significativo, almeno dal punto di vista dell’utilizzatore, dell’XFEM è che permette di modellare le discontinuità e il loro sviluppo senza che sia richiesta, per ogni avanzamento o modifica, la definizione di una nuova mesh. Tuttavia, bisogna pure ricordare che l’integrazione numerica degli elementi che vengono attraversati dalla discontinuità richiede una particolare trattamento. Il metodo più utilizzato a tal fine è quello di dividere l’elemento di interesse in due sottodomini rispetto alla linea della discontinuità. Tuttavia questo modo di procedere, pur flessibile, non è appropriato per materiali “history dependent”, per i quali la proiezione delle variabili dai vecchi ai nuovi puti di Gauss è inevitabile: sebbene siano stati proposti metodi alternativi al riguardo, manca ancora un approccio di validità generale che permetta di superare il problema. Un altro problema legato al XFEM è il fatto che, a causa dei gradi di libertà che vengono aggiunti, non è di facile implementazione nei codici commerciali. Sebbene siano state trovate soluzioni al riguardo e la necessità di introdurre nuovi gradi di libertà sia stata eliminata, i metodi elaborati risultano essere molto onerosi computazionalmente e ciò limita la loro appetibilità.
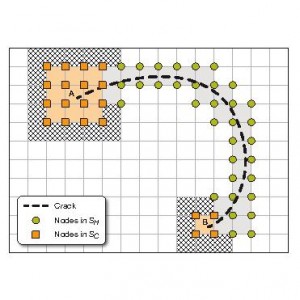
Alcune applicazioni
Come già sottolineato, aspetto peculiare del XFEM è il fatto che non è necessario modellare la discontinuità, il che lo rende particolarmente appetibile in tutti quei casi in cui si ha una geometria complessa insieme a una discontinuità, il che rende particolarmente arduo l’ottenimento di una mesh a elementi finiti adeguata e senza elementi eccessivamente distorti nelle zone critiche, requisito essenziale per ambire a risultati accurati. Proprio in questi casi spicca la peculiarità del XFEM, che non ha bisogno di modellare materialmente la discontinuità ma la implementa con il già menzionato arricchimento delle funzioni che descrivono il campo di spostamento.
Molti sono i problemi che sono stati affrontati e risolti con questo metodo: la propagazione quasi statica di fratture, in due e tre dimensioni, casi di frattura dinamici, cricche intersecantesi o che presentano biforcazioni. In figura 3 si vede un elemento criccato modellato con XFEM: si può mostrare che si ottengono risultati accurati senza dover infittire il modello in corrispondenza della discontinuità.Un altro interessante campo di applicazione sono le analisi fluidodinamiche, in cui all’interfaccia tra fluidi differenti possono nascere discontinuità. In Figura 4 è mostrato l’esempio un’onda raggiunge una struttura elastica. Il dominio fluido è separato in due aree (acqua e aria) che differiscono per viscosità e densità: in questo caso è il cambiamento repentino e discontinuo delle diverse grandezze di campo attraverso l’interfaccia viene considerata implicitamente nell’XFEM. Per l’interfaccia tra i fluidi e la struttura si definisce esplicitamente la mesh a la si considera nel modo usuale.
Infine, alcune recenti applicazioni mostrano un proficuo utilizzo dell’XFEM per modellare le interfacce tra giunzioni ibride, in cui i materiali sono compositi a matrice polimerica e metali).

Conclusioni
Il metodo XFEM rappresenta oggi un approccio maturo per la simulazione di problemi che includono discontinuità. A fronte di una complessità matematica superiore, dal punto di vista dell’utilizzatore risulta essere molto più semplice, in quanto non richiede di modellare la discontinuità stessa, elemento spesso causa di problemi nella tradizionale modellazione a elementi finiti. Oggigiorno i più diffusi codici commerciali a elementi finiti già hanno la possibilità di utilizzare routine che fanno riferimento a questo metodo, il cui utilizzo, verosimilmente, è destinato ad aumentare insieme alla complessità dei problemi ingegneristici.





