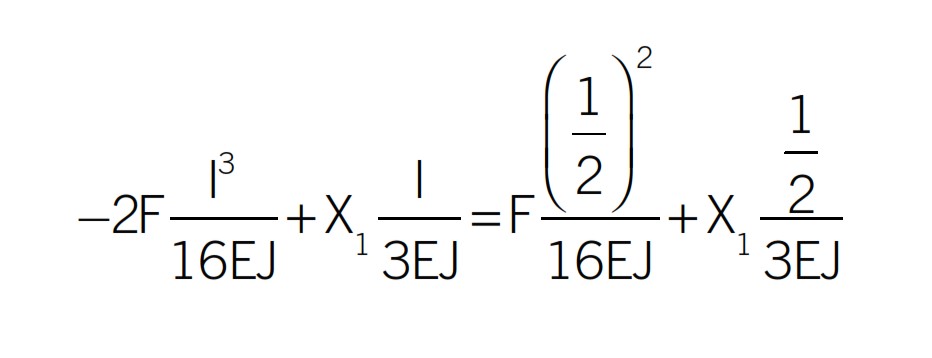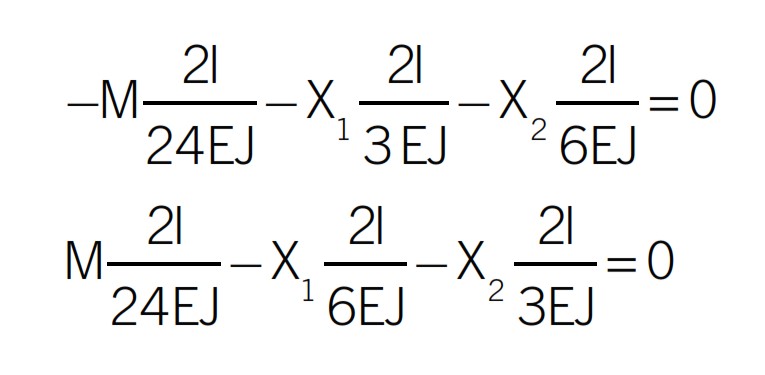Il metodo delle forze per la soluzione di strutture iperstatiche in questa puntata dei Quaderni di Progettazione di Franco Concli.
Sebbene le regole della buona progettazione raccomanderebbero di progettare ogni struttura come isostatica, nella pratica spesso si hanno strutture iperstatiche. Sebbene oggigiorno le tecniche numeriche come gli elementi finiti ne premettono comunque la soluzione in modo relativamente semplice, può essere utile conoscere anche un metodo analitico: il metodo delle forze.
Il metodo delle forze è uno strumento molto potente che permette non solo di risolvere strutture una o più volte iperstatiche, ma anche di calcolarne spostamenti, rotazioni ecc.
Il metodo si basa sul principio dei lavori virtuali. Esso completa le equazioni di equilibrio statico mediante condizioni ausiliarie che permettono di compensare l’indeterminazione che si avrebbe a causa del numero di incognite maggiore del numero di equazioni indipendenti a disposizione. Il metodo fu introdotto nel XIX secolo da Mueller-Breslau.
Il metodo usa una formulazione in termini di sforzi e ricerca la soluzione tra tutti i possibili campi di tensioni generalizzate in equilibrio con i carichi esterni a cui corrispondono deformazioni generalizzate e spostamenti compatibili con i vincoli cinematici del sistema.
Il metodo delle forze per le strutture iperstatiche
Il metodo si basa sul principio di sovrapposizione degli effetti. Nel caso di sistema iperstatico, a questo viene associato un secondo sistema, detto virtuale, che, a differenza del primo, deve essere staticamente determinato.
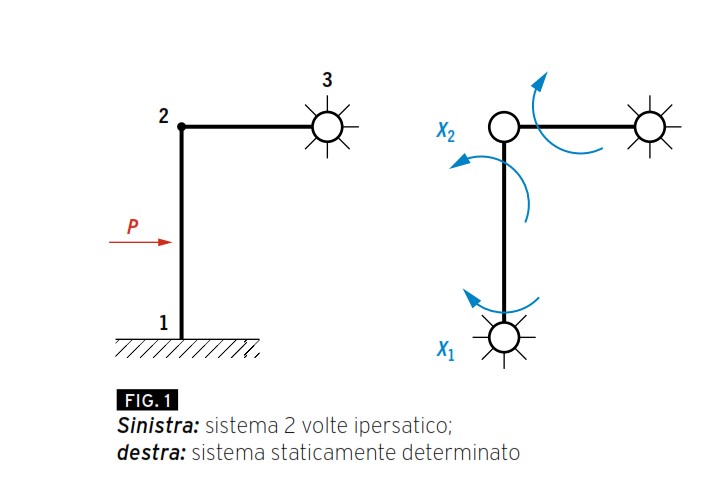
In Figura 1 viene mostrato un esempio di sistema due volte iperstatico (una asta nel piano = 3 gdl, un incastro = 3 gdv, una cerniera = 2 gdv) e come questo possa essere trasformato in un sistema staticamente determinato mediante l’introduzione di una cerniera interna e degradazione dell’incastro a cerniera. In viola vengono messe in evidenza le incognite iperstatiche.
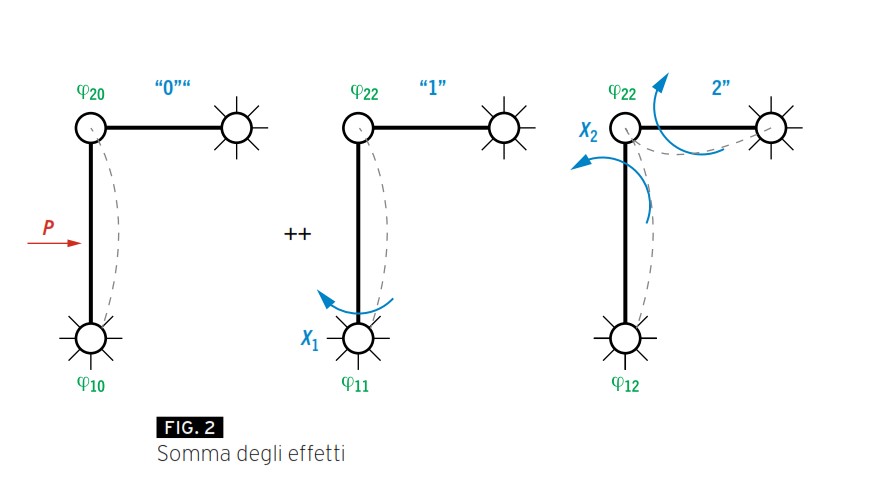
Figura 2 mostra il sistema reso staticamente determinato visto come la somma degli effetti delle forze esterne P e delle due incognite iperstatiche X1 ed X2.
In verde in Figura 2 sono mostrate le rotazioni dovute ai vari carichi. φ12, ad esempio, rappresenta la rotazione dell’asta al nodo 1 (si veda Figura 1) per effetto della incognita iperstatica X2 (presa unitaria).
Dati M0, M1 ed M2 (azioni interne) per effetto rispettivamente di P, X1 ed X2, le azioni interne M che agiscono sulla struttura reale possono essere calcolate come la somma di M0, M1 ed M2.
M = M0 + M1 + M2
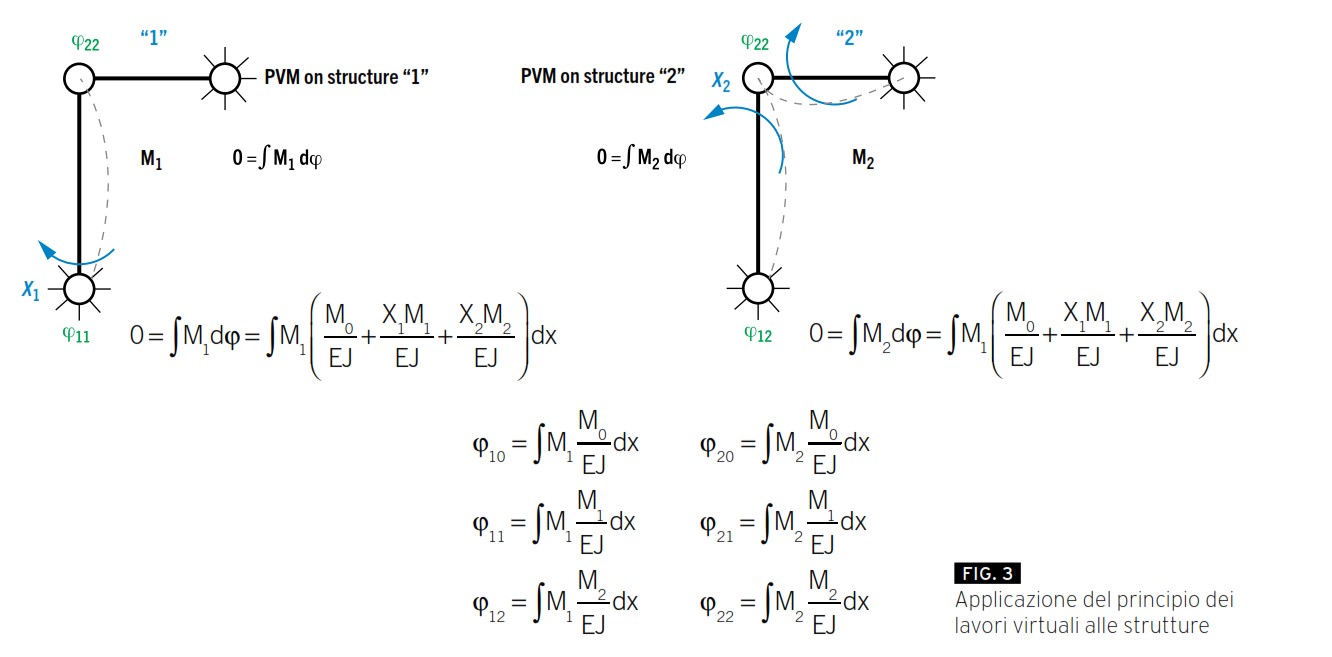
Per il calcolo di M1 ed M2 ci si potrebbe basare sull’applicazione del principio dei lavori virutali sapenso che la somma dei lavori esterni deve essere uguale a quella dei lavori interni.
Come si vede da Figura 3, l’applicazione del principio dei lavori virtuali porta a dover scrivere equazioni la cui risoluzione non è banale.
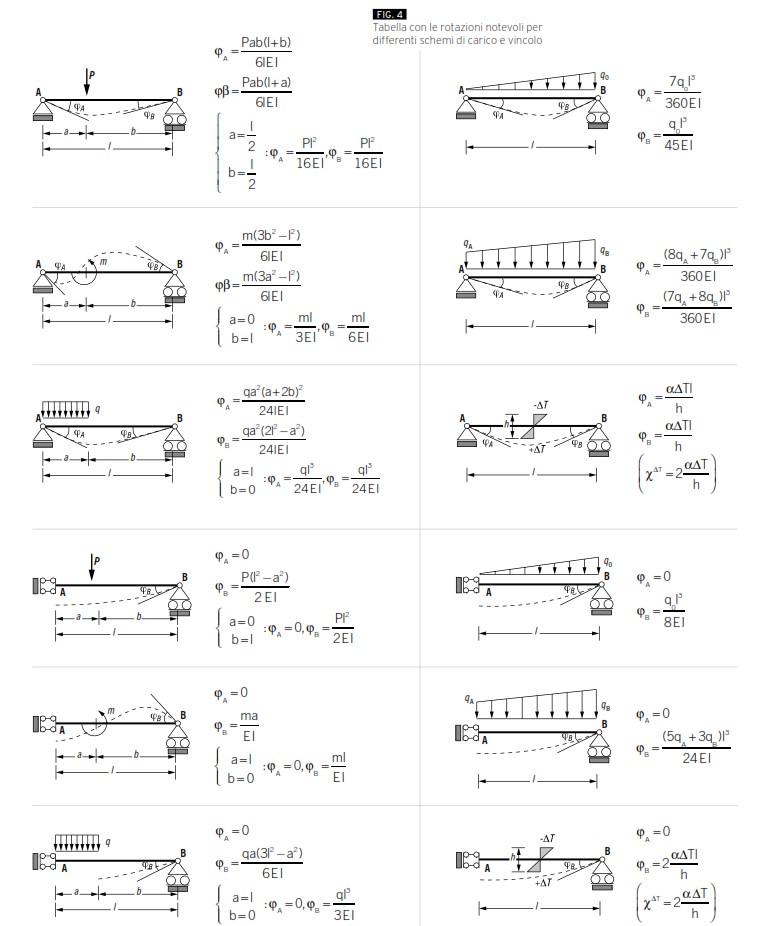
Nella pratica quindi, risulta più comodo prendere valori tabellati per quanto riguarda le rotazioni φ. Esistono infatti tabelle che riportano le rotazioni notevoli Ψ per differenti condizioni di vincolo e per carichi unitari.
Sarà quindi possibile scrivere semplicemente
φ10 = φ11 + φ12 = Ψ11X1 + Ψ12X2
φ20 = φ21 + φ22 = Ψ21X1 + Ψ22X2
in cui i valori Ψ sono presi da tabella.
Utilizzo pratico del metodo
Per meglio spiegare l’utilizzo pratico del metodo si introdurranno un paio di esempi.
Esempio 1x iperstatica
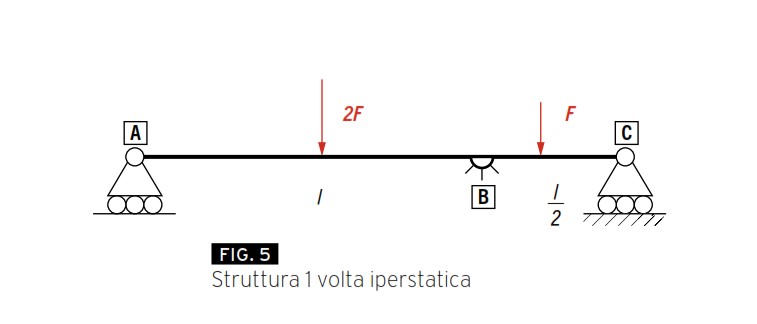
La Figura 5 mostra una trave di lunghezza 3/2l supportata da due carrelli ed una cerniera.
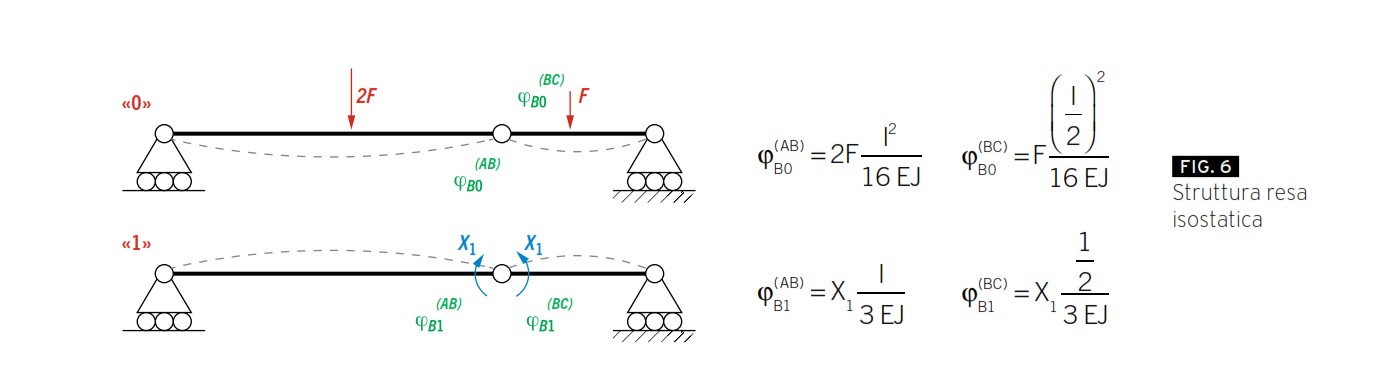
La procedura di soluzione prevede il passaggio dalla struttura iperstatica alla struttura virtuale resa isostatica. Figura 6 mostra la struttura virtuale caricata una volta con i soli carichi esterni F e 2F e una volta con la sola incognita iperstatica X1.
Le rotazioni agenti nei vari nodi e sulle varie aste sono messe in evidenza in verde. Il pedice fa riferimento al nodo e al carico, l’apice all’asta (ad esempio φB1(AB) fa riferimento alla rotazione indotta dal carico 1, ovvero l’incognita iperstatica X1 sul nodo B e sull’asta AB). I valori riportati in Figura 6 son presi dalla tabella di Figura 4. La trave AB, ad esempio, è supportata da cerniera e carrello. Se sottoposta ad una coppia m (nel nostro caso X1) agente nel nodo di destra ruoterà corrispondentemente del valore l/3EJ in cui l è la lunghezza della trave, E il modulo elastico del materiale e J le proprietà inerziali della sezione (figura nella seconda riga a sinistra in Figura 4). Note le rotazioni è possibile scrivere l’equazione di congruenza del nodo B.
da cui
X1 = 9/32 Fl
Esempio 2x iperstatica
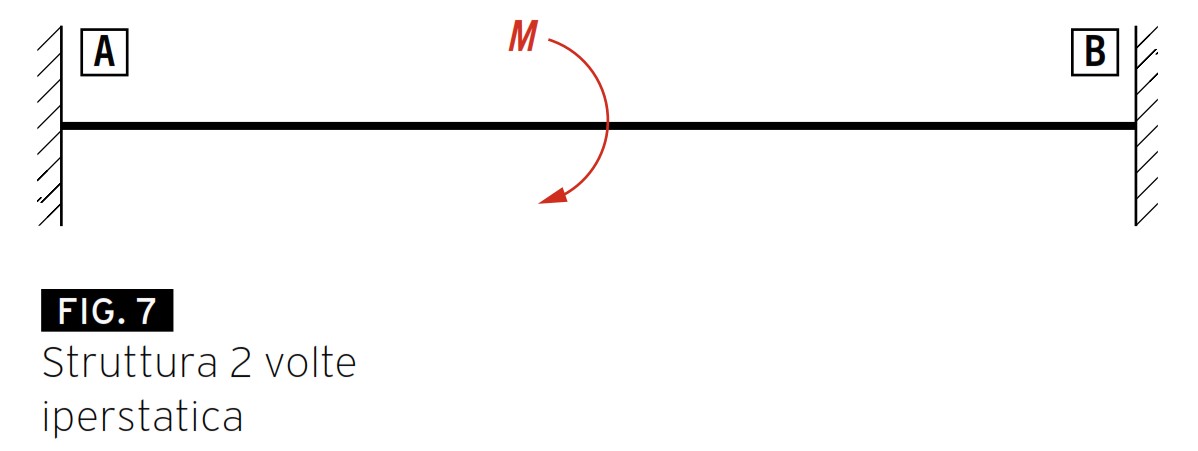
Figura 7 mostra un altro esempio. Questa volta la struttura risulta due volte iperstatica e pertanto sarà necessario degradare due vincoli.
Nello specifico i due incastri sono stati sostituiti da due cerniere. Si avranno pertanto tre strutture isostatiche, una su cui agiranno i soli carichi esterni (M), una su cui agirà l’iperstatica X1 ed una su cui agirà l’iperstatica X2.
Anche in questo caso le rotazioni notevoli per carichi unitari Ψ possono essere prese dalla tabella in Figura 4. Moltiplicate per M, X1 o X2 daranno le relative rotazioni φ. Note tutte le rotazioni si passa alla scrittura delle equazioni di conseguenza nei due nodi.
che portano a
X1=-M/4
X2=M/4
Esempio 2x iperstatica con cedimento di vincolo e carico termico
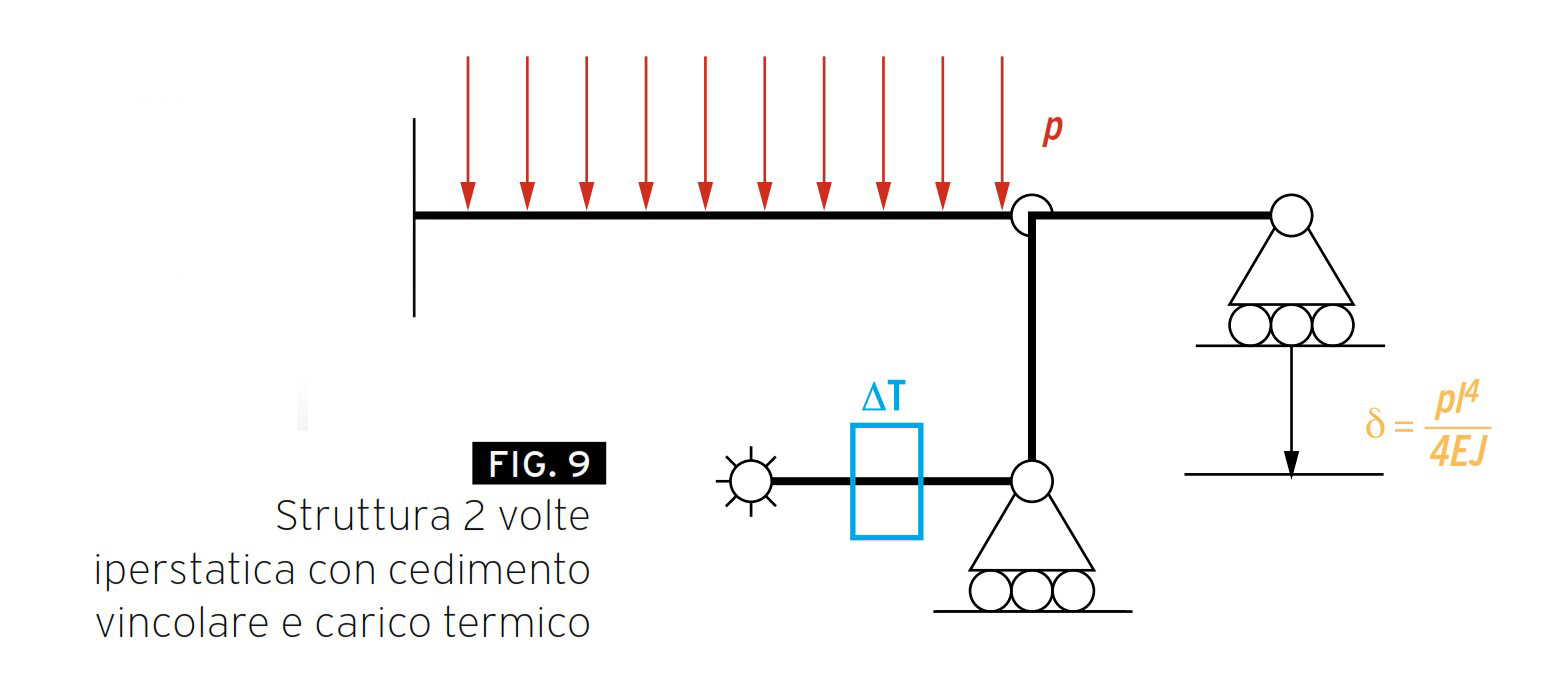
Come ultimo esempio si consideri la Figura 9. Si tratta di una struttura 2 volte iperstatica con un cedimento vincolare δ noto e pari a pl4/4EJ ed un carico termico ΔT.
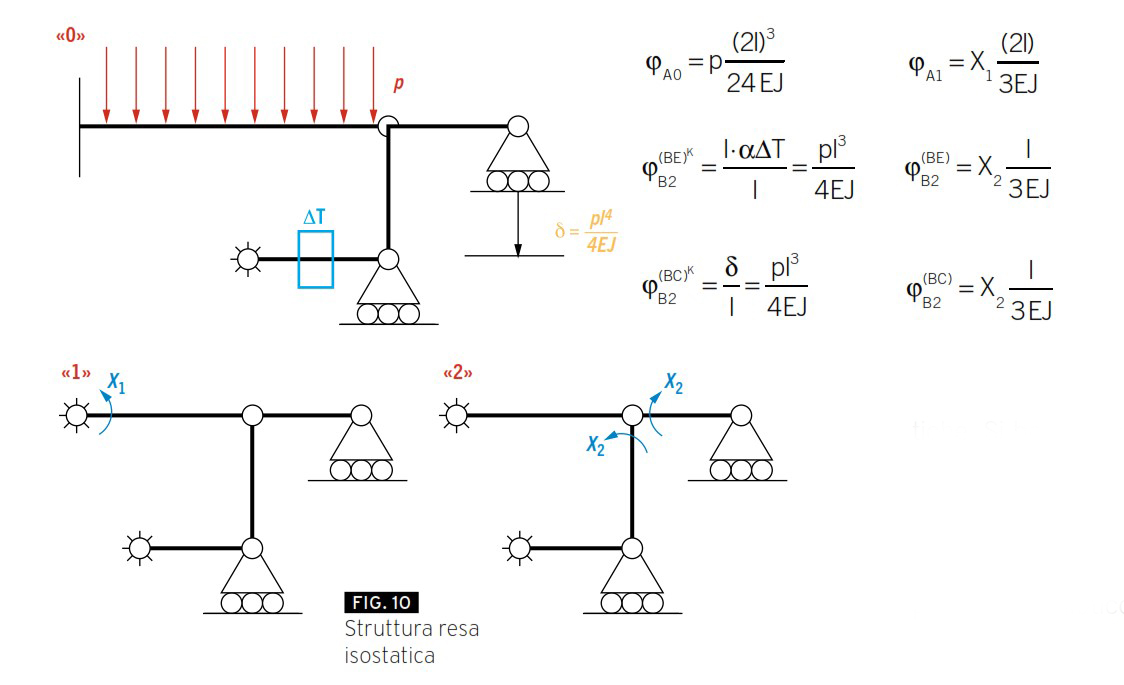
Anche in questo caso la struttura va resa isostatica e l’effetto dei carichi esterni e delle incognite iperstatiche messo in evidenza in modo separato.
La congruenza può essere scritta nei nodi A e B. La presenza del cedimento di vincolo e del carico termico provoca anch’essa delle rotazioni. Attenzione a tenerne conto. In particolare il carico termico porterà ad una rotazione aggiuntiva dell’asta BE (φB2(BE)k ) mentre il cedimento di vincolo porterà una rotazione aggiuntiva dell’asta BC (φB2(BC)k )(Figura 10).
Le incognite iperstatiche risultano
X1=pl2/2
X2=3pl2/4
Conclusioni
Il metodo delle forze è uno strumento molto potente per il calcolo delle incognite iperstatiche. Si basa sul principio dei lavori virtuali ma permette una risoluzione molto rapida del sistema grazie alla necessità di scrittura delle sole equazioni di congruenza. Le rotazioni possono essere prese facilmente da tabella per cui anche la soluzione di un sistema più volte iperstatico richiede pochi minuti.