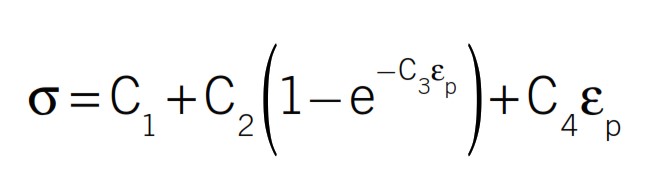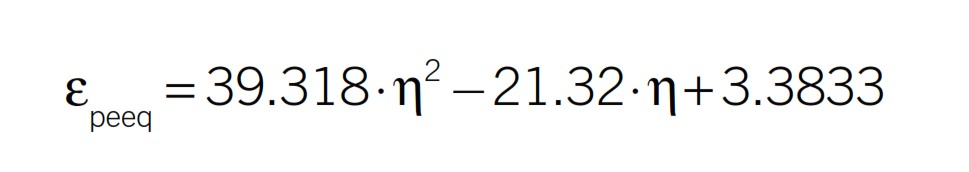Il presente articolo mostra come caratterizzare il locus di frattura di un materiale tarando un modello di danneggiamento duttile. Nello specifico vengono riportati i risultati per un acciaio CORTEN. Il materiale è stato caratterizzato attraverso test sperimentali quasi statici su provini aventi geometrie diverse e, quindi, diversi livelli di triassialità. Le configurazioni testate sono state riprodotte numericamente mediante modellazione agli elementi finiti utilizzando il software open-source Code_Aster.
Autori: F. Concli, L. Maccioni
Nei primi anni Trenta negli Stati Uniti è stato lanciato un nuovo materiale in grado di resistere alle intemperie ed all’azione dell’ambiente esterno (Decker et al., 2008). Per sottolineare la sua resistenza a CORrosione e le ottime proprietà a trazione (TENsile), l’acciaio basso legato auto-passivante è stato chiamato CORTEN. La sua composizione ha subito molte modifiche negli anni (Revie, 2011) e oggigiorno, in Europa, questi acciai sono delineati nella norma DIN EN 10020.
Le sue caratteristiche di resistenza, paragonabili a quelle di altri acciai da costruzione (resistenza tipicamente compresa tra 235 e 355 MPa), non sono però la caratteristica che ne ha permesso la rapida diffusione. In effetti, il CORTEN fu inizialmente sfruttato nel settore ferroviario (Dunkley, 1967) per ridurre gli effetti degli agenti atmosferici sui vagoni. È stato utilizzato anche nella costruzione di ponti (Fischer, 1995) con l’obiettivo di superare la necessità di verniciature e manutenzioni periodiche. Per motivi estetici, la sua applicazione è stata introdotta nelle facciate di edifici (Mostafavi e Leatherbarrow, 1993) ed utilizzata per molte opere d’arte all’aperto (Riferimento Web 1).
Il comportamento alla corrosione CORTEN è stato validato in diversi ambienti (Kamimura et al., 2006; Mocillo et al., 2013). Esso richiede cicli umidi/asciutti per riuscire a creare lo strato protettivo caratteristico (Schmitt e Gallagher, 1969). Inoltre, in ambiente marino, il fenomeno di auto-passivazione è influenzato negativamente dalla presenza di Cl– (Zhang et al., 2013). In ambiente inquinato, il processo di passivazione, specialmente in presenza di elevata umidità, è impedito dal biossido di zolfo SO2 (Wang et al., 1997).
Al giorno d’oggi, i guardrail dell’autostrada del Brennero e molte strade locali della regione alpina dell’Alto Adige sono fatti in CORTEN. Questo perché il colore naturale di questo acciaio (marrone) garantisce un basso impatto visivo delle barriere in una zona patrimonio mondiale dell’UNESCO. In secondo luogo, i bassi (previsti) costi di manutenzione hanno favorito il suo sfruttamento.
Nonostante i test di omologazione siano obbligatori e ben definiti, in alcune aree specifiche le protezioni in CORTEN non sono totalmente esenti da corrosione (Deflorian e Rossi, 2002). Pertanto, è possibile che le capacità di resistenza ed assorbimento di energia siano compromesse dalla mancanza di passivazione e dalla conseguente corrosione.
Per meglio caratterizzare le prestazioni di sicurezza dei parapetti in CORTEN mediante simulazioni di crash ad elementi finiti, è essenziale prima di tutto caratterizzare la legge costitutiva (Whitworth et al., 2004) e mettere a punto un modello di danneggiamento duttile (locus di frattura) del materiale (Ren e Vesenjak, 2005). Con questi dati i modelli FE potrebbero essere utili anche per la ricostruzione di eventi di incidente.
Il comportamento duttile del CORTEN è stato caratterizzato sulla base di test sperimentali quasi statici condotti su provini di diverso spessore ed aventi geometrie diverse – quindi diversi livelli di triassassialità (Concli e Maccioni, 2019). I diversi spessori sono stati scelti per evidenziare eventuali effetti del processo di laminazione sul comportamento duttile di CORTEN. Inoltre, i test sono stati riprodotti numericamente, per determinare lo stato di sollecitazione e quantificare la deformazione plastica alla rottura per calibrare un modello di danneggiamento duttile.
Calibrazione del modello di danneggiamento duttile
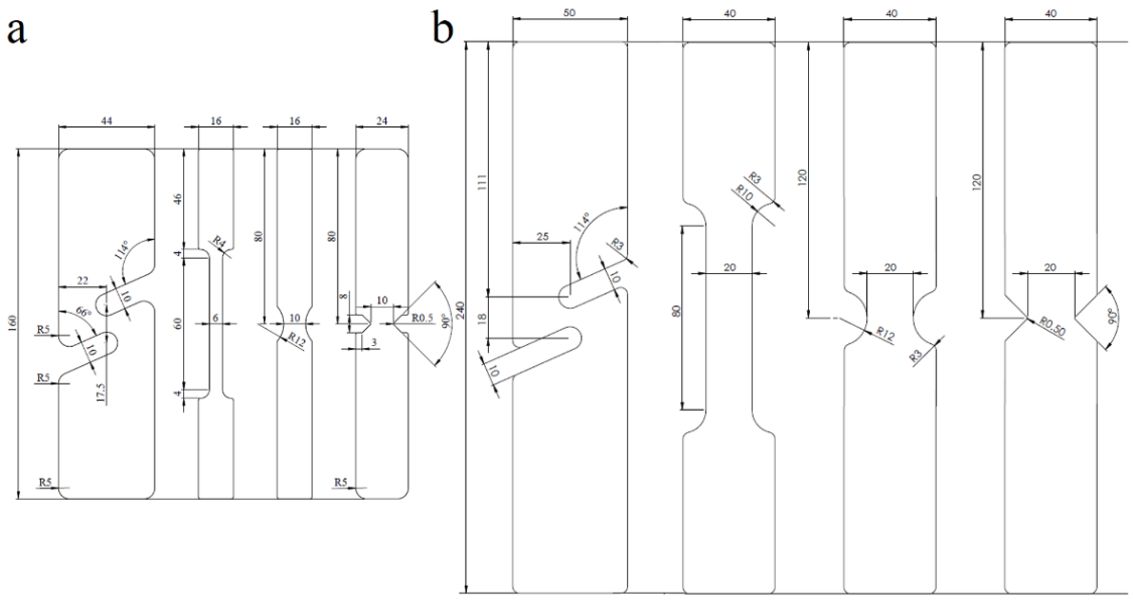
In questo studio sono state utilizzate due serie di campioni realizzati in CORTEN (S355J0WP). 4 differenti geometrie sono state tagliate al laser da fogli di lamiera di spessore 8 mm e 2 mm (Figura 1).
Su tali provini sono stati eseguiti test di trazione su una macchina di prova MTS Criterion 45 in grado di applicare carichi fino a 100 kN. Sono stati acquisiti la forza applicata e lo spostamento della traversa. Nei test sui due provini (spessore 2 e 8 mm) non intagliati (#2.1, #2.2) è stata acquisita anche la deformazione, misurata tramite un estensimetro.
La legge costitutiva può essere descritta attraverso l’equazione sottostante, legge Voce (Voce, 1948; Voce, 1955). Le costanti possono essere ricavate attraverso una procedura numerica inversa.
Le costanti Ci rappresentano rispettivamente lo snervamento, un coefficiente lineare, un coefficiente esponenziale ed il cosiddetto parametro di saturazione esponenziale.
è la deformazione plastica accumulata.
Per ogni geometria è stata fatta la relativa simulazione numerica. La curva F-s (Forza – spostamento della traversa) ottenuta numericamente è stata confrontata con quella sperimentale (misurata) in una procedura iterativa che ha permesso di trovare la legge costitutiva che desse il fit migliore tra curve sperimentali e numeriche.
Nel corso degli anni, sono stati condotti molti studi sul danneggiamento duttile. Rice e Tracey (1969) furono i pionieri e proposero un modello che legava la triassialità dello sforzo al cedimento dei metalli (funzione esponenziale decrescente). Ulteriori modelli furono sviluppati da Hancock e Mackenzie (1976) che inclusero gli effetti della temperatura e della velocità di deformazione. Ulteriori miglioramenti furono proposti da Johnson and Cook (1983) e Mirza et al. (1997). In tutti questi modelli, la deformazione plastica alla frattura è una funzione della triassialità dello sforzo η, definita come in questa equazione:
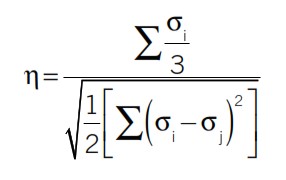Tuttavia, studi condotti da Bao (2003), Bao e Wierzbicki (2004), Bao (2005) e Gilioli et al., (2015) hanno mostrato come il legame deformazione plastica – triassialità non possa essere modellato con una funzione monotona. Suárez et al. (2018) hanno proposto una modellazione del locus di frattura mediante tre principali regioni associate a diversi meccanismi di cedimento (Figura 3).
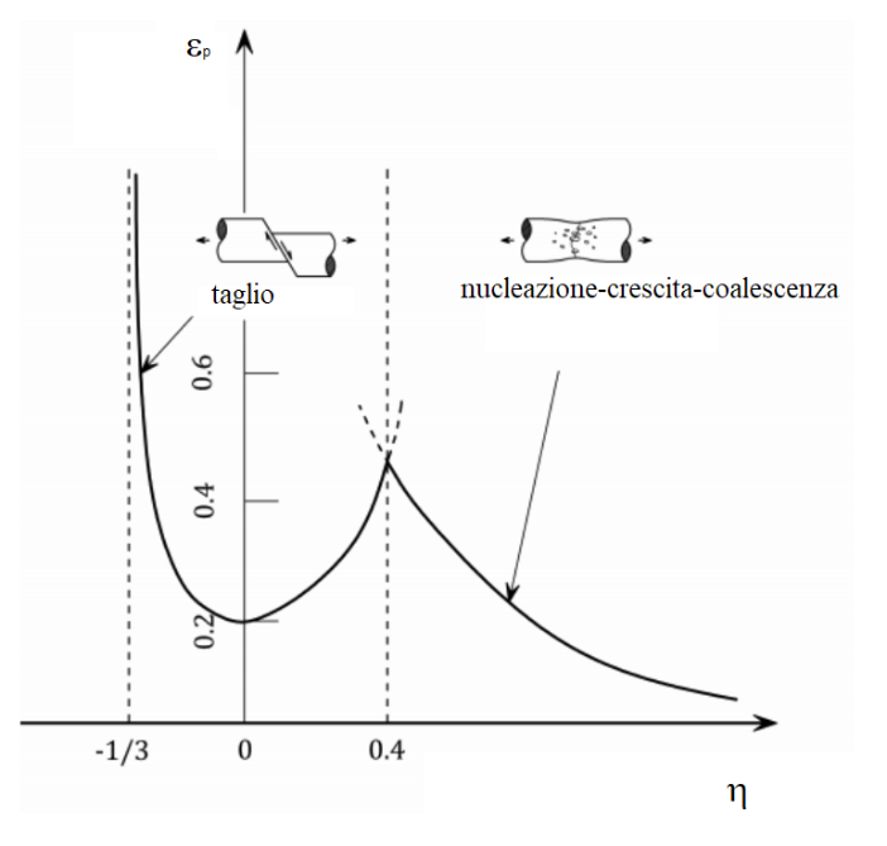
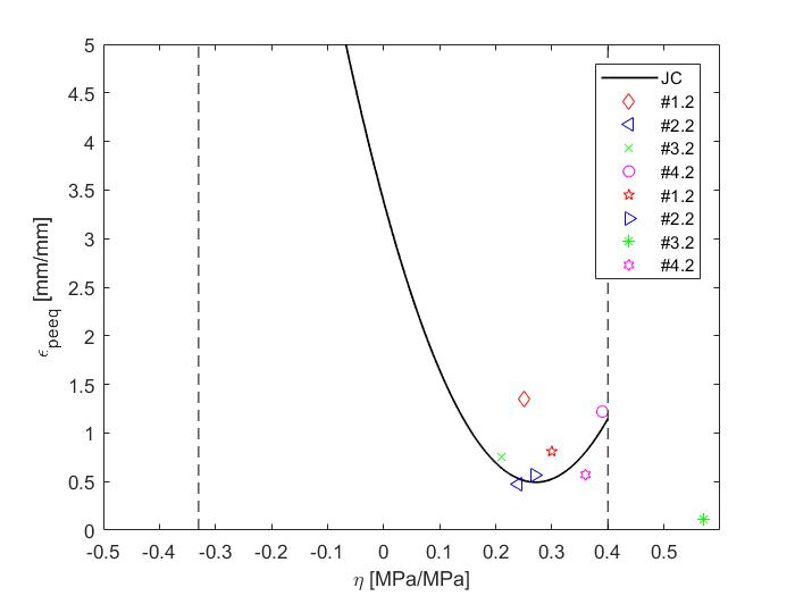
Per valori di triassialità negativi, il taglio sembra essere il principale meccanismo di cedimento; per valori di triassialità elevati (> 0.4), il principale meccanismo di cedimento risulta la nucleazione-crescita-coalescenza. Per valori intermedi di triassialità si ha una combinazione di questi due meccanismi. Nel seguito si andrà a studiare proprio questa regione intermedia.
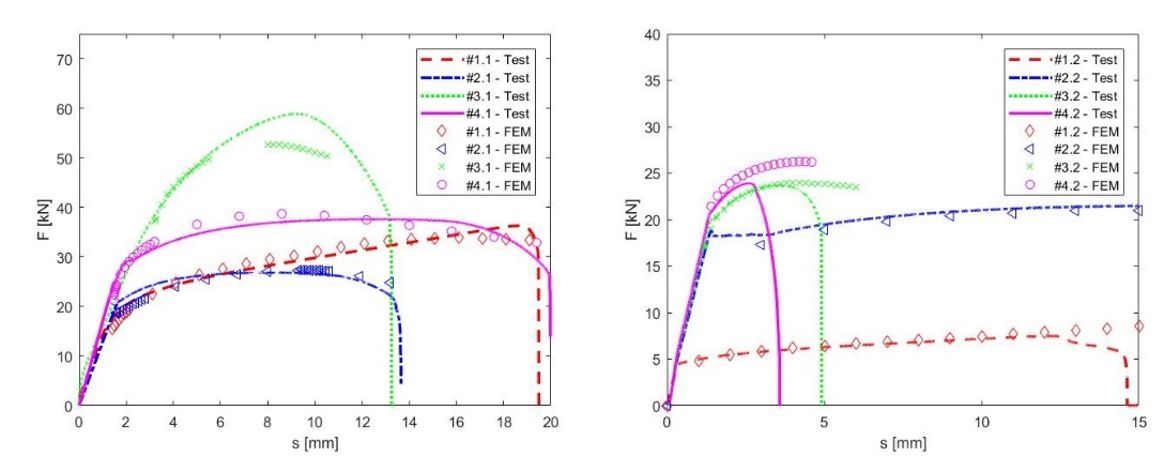
Figura 2 mostra le geometrie dei provini utilizzate per la calibrazione del locus di frattura. Ogni provino è stato portato a rottura mediante trazione. Per mezzo del software gratuito open source Code_Aster, le configurazioni di prova sono state riprodotte numericamente come descritto in (Concli e Gilioli, 2019; Concli et al., 2019).
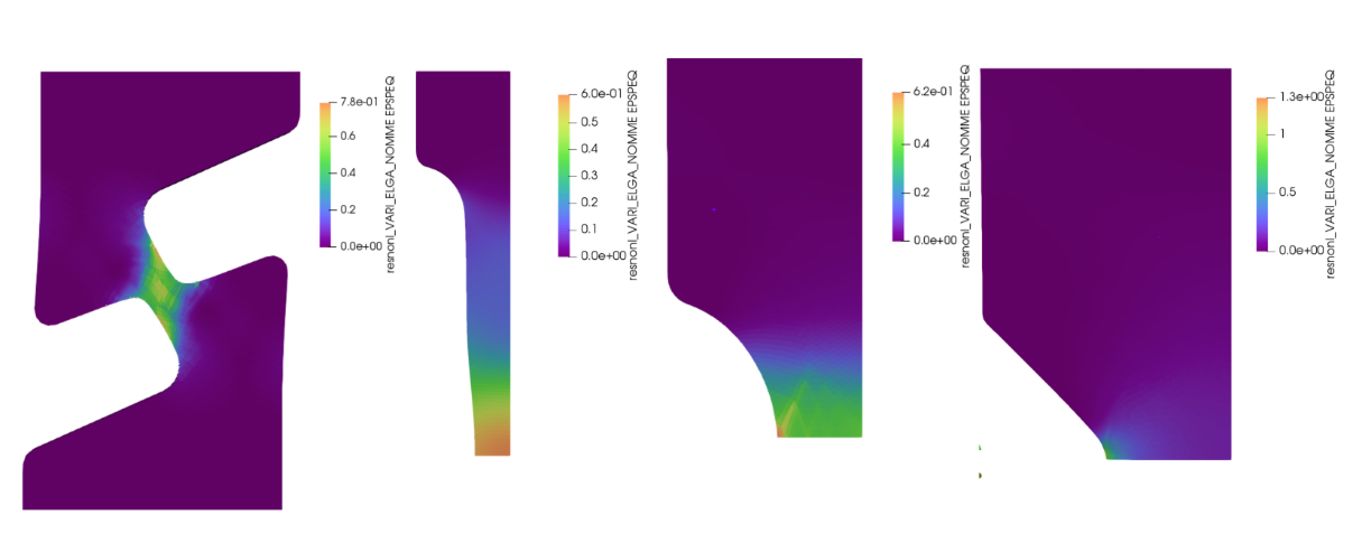
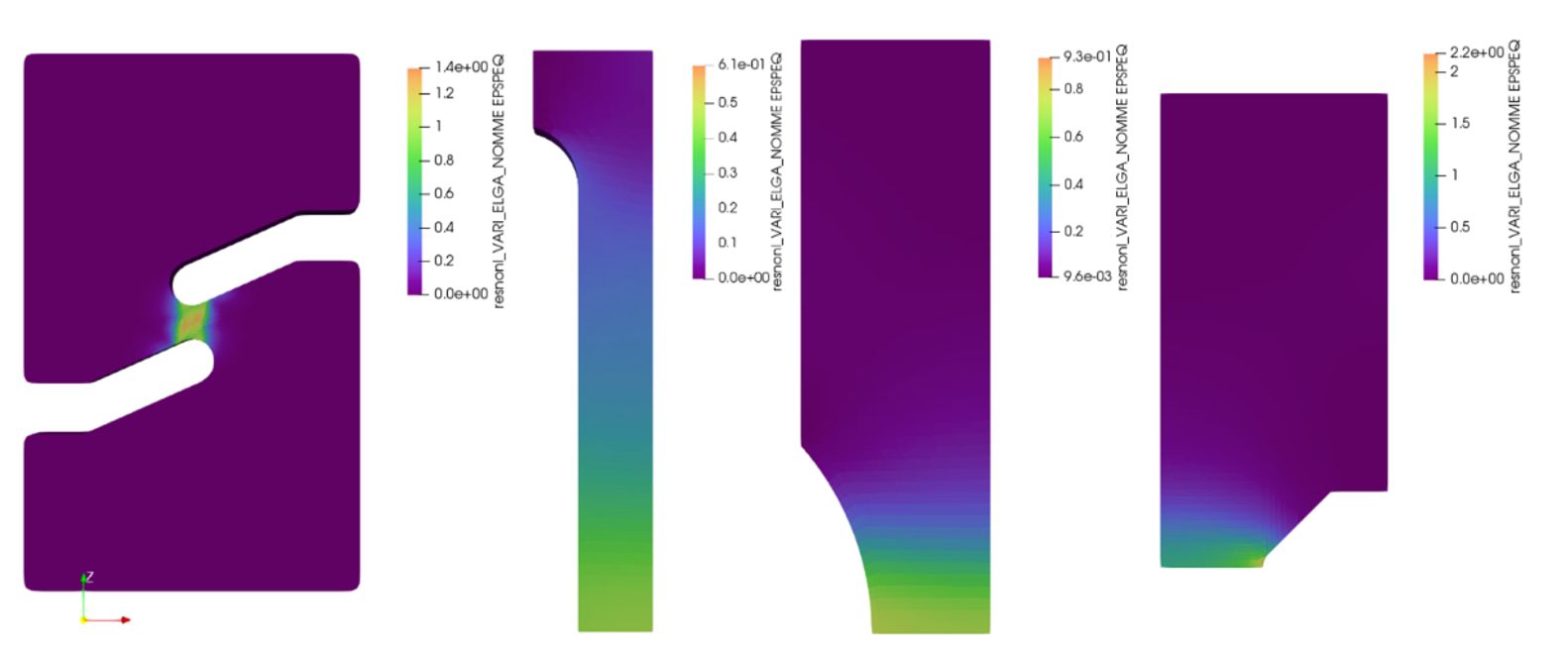
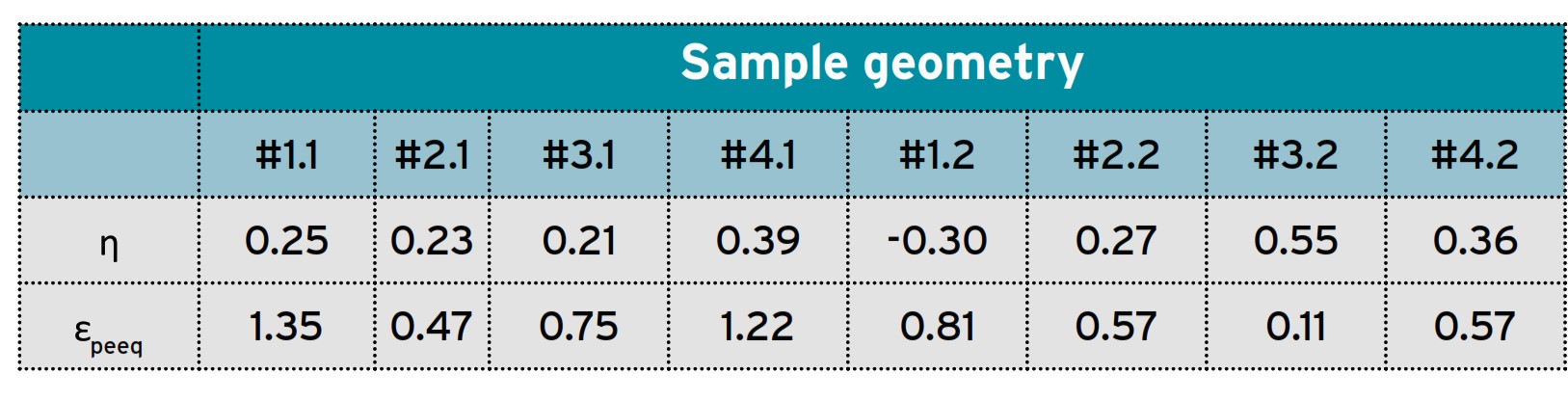
Per la calibrazione del modello di danneggiamento duttile si è sfruttato un software open source poiché l’assenza di licenze consente calcoli altamente parallelizzati. Le simulazioni sono state eseguite imponendo lo spostamento (traversa) che sperimentalmente ha portato al cedimento (Figura 4 e Figura 5). (deformazione plastica equivalente a frattura) e (triassialità nel punto di rottura) sono state ottenute dalle simulazioni numeriche (Figura. 6).
I valori sono riportati nella tabella sottostante.
Dopo un’interpolazione ai minimi quadrati, l’equazione che descrive il locus di frattura risulta:
Figura 6 mostra i 7 punti che ricadono nell’intervallo di triassialità intermedio (0 ÷ 0.4). È possibile notare come la dispersione dei punti (ad eccezione del provino #1.2 che non ricade nell’intervallo) segua bene la funzione quadratica proposta da Johnson & Cook.
Per completezza, sono state eseguite anche misure tramite DIC (Digital Image Correlation). La DIC è un metodo ottico in grado di misurare il campo di spostamento. Prima di ogni test, i provini sono stati preparati creandovi una trama superficiale mediante verniciatura. L’immagine del campione è stata acquisita durante le prove sperimentali per mezzo di una fotocamera reflex da 32 MPixel. Le immagini venivano acquisite ogni 3 s (corrispondenti a 0,05 mm di spostamento della traversa). Il confronto tra le coordinate xi, yj del campione indeformato e xi*, yj* ad un determinato istante temporale hanno permesso la ricostruzione dello spostamento e, quindi, del campo di deformazione ad ogni time step.
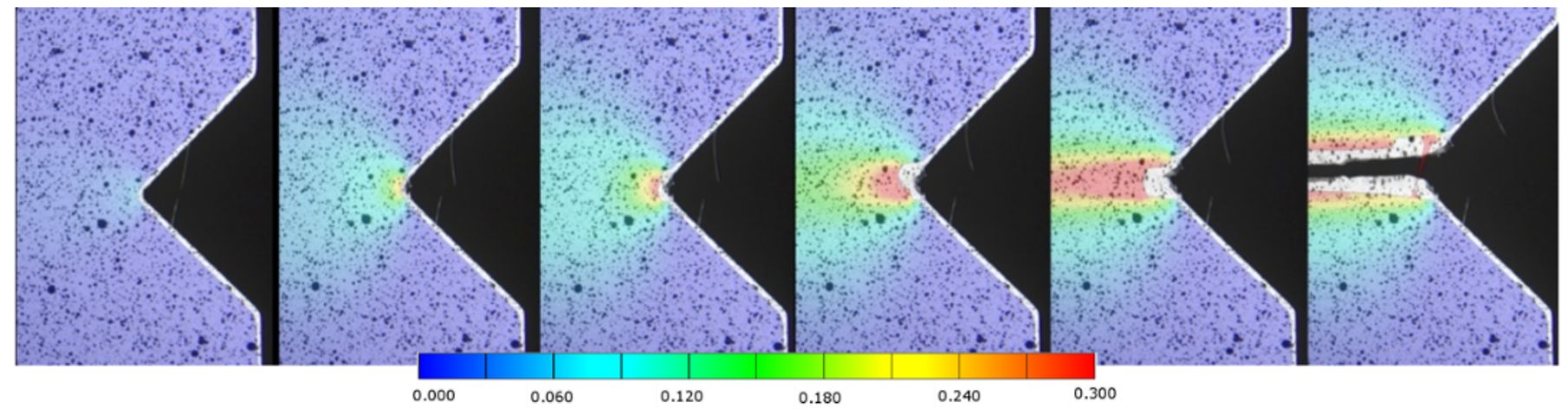
Figura 7 mostra le deformazioni del campione #4.2 elaborate tramite DIC. Sul lato destro si può notare come, dopo il cedimento, nel materiale rimangano grandi deformazioni plastiche residue.
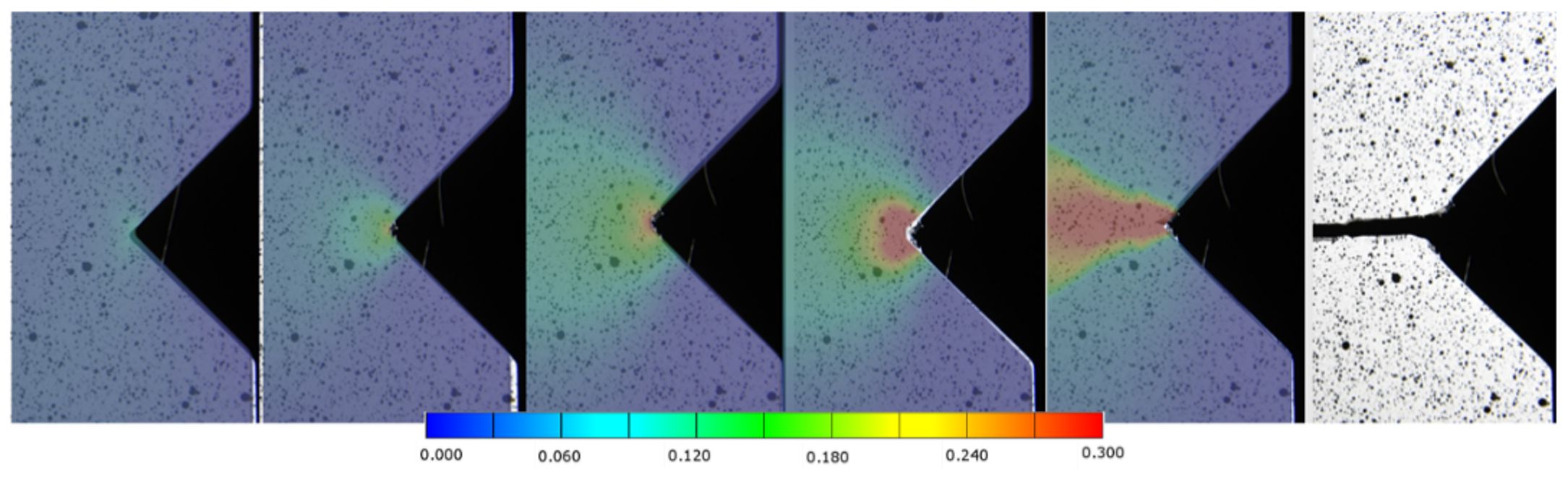
Figura 8 riporta le deformazioni calcolate numericamente sovrapponendole alle immagini reali del campione. I campi di deformazione sono comparabili solo per le prime tre immagini, vale a dire prima della fessurazione del materiale. Il modello FEM, infatti, non considerava la cricca: nel modello numerico la parte superiore e quella inferiore del campione rimangono collegate; di conseguenza, i campi di deformazione risultano diversi rispetto a quelli ottenuti mediante DIC. A questo proposito, un modello FE con la possibilità di distacco degli elementi della griglia una volta superato localmente il limite (Fig. 6), garantirebbe un campo di deformazione più realistico (Concli e Gilioli, 2018).
Conclusioni
In questo studio, è stato calibrato il modello di frattura duttile proposto da Johnson and Cook (1983) per un acciaio CORTEN (S355J0WP). La legge costitutiva è stata trovata attraverso una procedura iterativa. Successivamente, il locus di frattura è stato calibrato sulla base di sette provini diversi per spessore e geometria. È stato utilizzato un software FEM open source: Code_Aster.
L’effetto della temperatura e della velocità di deformazione sono stati trascurati. Alcuni test preliminari hanno mostrato una leggera anisotropia nel CORTEN (lamiera spessa 2 mm) a seconda della direzione di laminazione. Pertanto, ulteriori studi saranno condotti su campioni a basso spessore, tagliati dallo stesso foglio di lamiera, ma in direzioni differenti. I risultati riportati fanno riferimento a test condotti su campioni non ancora passivati; un ulteriore passo sarà la ripetizione della procedura su campioni passivati.
Ringraziamenti
Si desidera ringraziare per questo articolo sulla calibrazione del modello di danneggiamento duttile A.ERRE Srl di Serravalle Pistoiese (PT) Italia http://www.aerrecarpenteria.it/ per il sostegno.
È possibile richiedere la Bibliografia completa contattando la redazione a questo indirizzo: emanuela.bianchi@tecnichenuove.com. Su richiesta sarà inviata per intero via mail.
