Numerosi sono i testi che trattano della progettazione delle molle a elica cilindrica, ma a trattazione delle molle coassiali viene spesso tralasciata o relegata ad un paragrafo in secondo piano. In realtà in moltissimi casi utilizzare una soluzione di questo tipo comporta un notevole risparmio di spazio, in particolare in quei casi in cui la lunghezza a pacco è il fattore limitante
Davide Crivelli
Le molle a elica sono composte da avvolgimenti di fili a sezione circolare o rettangolare attorno ad un cilindro, cono o ad una superficie qualsiasi. Chiaramente, per ragioni di semplicità costruttiva, si utilizzano principalmente molle ad elica cilindrica o in rari casi conica. Gli avvolgimenti, che normalmente hanno passo costante, possono essere disposti sia in senso orario che in senso antiorario.
Fra i vantaggi delle molle a elica vi sono il basso costo e la flessibilità di utilizzo. Modificando le configurazioni e la lunghezza questi componenti possono essere adattati facilmente agli spazi disponibili, e non richiedono tolleranze precise di allineamento assiale, in quanto le loro caratteristiche di elevata elasticità ne consentono il recupero autonomo.
La progettazione di molle a elica cilindrica è trattata in numerosi testi e manuali, per cui non ne riprenderemo i principi in queste pagine. È pratica consolidata procedere con un dimensionamento di tipo iterativo, in quanto il metodo è facilmente implementabile e richiede pochi dati in ingresso: le caratteristiche del materiale, il carico assiale, la rigidezza desiderata. Tuttavia, questo metodo non permette di conoscere a priori gli ingombri caratteristici delle molle (diametro esterno e lunghezza a pacco), perché si basa sull’imposizione del diametro medio dell’avvolgimento. Questo è un problema nel caso di applicazioni con ingombro diametrale limitato da vincoli esterni (ad esempio contenitori) o interni (steli, pistoni) cui bisogna sottostare.
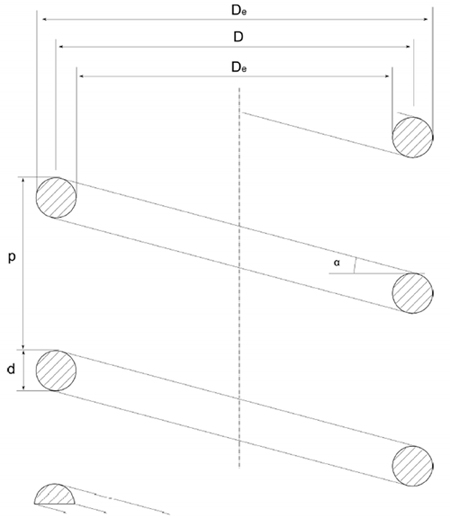
Dimensionamento a partire dal diametro esterno
Quando il diametro esterno è un fattore vincolante, il progettista si trova a dover iterare più volte il calcolo della molla, generalmente svolto a partire dal diametro medio di avvolgimento. Questo porta ad arrivare a compromessi, che, se pur accettabili, sono sempre peggiorativi: a parità di rigidezza infatti la molla di maggior diametro permette di ottenere la stessa rigidezza con un diametro di filo minore. Inoltre questo tipo di dimensionamento è fondamentale per il calcolo dei pacchi di molle coassiali, in cui il diametro esterno della molla interna è limitato dal diametro interno della molla esterna.
Il dimensionamento è facilmente impostabile dalle equazioni (1) e (2) noto lo sforzo ammissibile, il carico massimo e il diametro esterno. Il progettista non si faccia spaventare dalla complessità apparente della formula, perché i moderni fogli di calcolo sono in grado di calcolare equazioni ben più complesse.
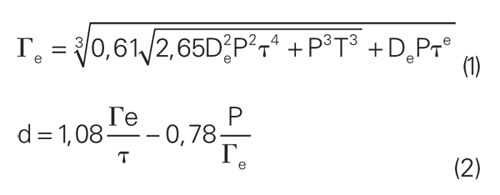
Una volta ricavato il diametro del filo si ricava il diametro medio di avvolgimento D e il numero di avvolgimenti n dalla seconda equazione del sistema (3).
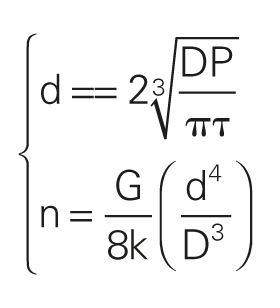
Ingombro longitudinale
L’ingombro longitudinale è un’altra caratteristica geometrica rilevante di una molla.
La lunghezza a pacco, che governa la lunghezza totale della molla, è funzione del prodotto d * n. Fissati i valori di progetto, si dimostra facilmente che per ottenere la molla di minima lunghezza sia opportuno aumentare, per quanto possibile, l’ingombro diametrale.
Pacchi di molle coassiali
Le molle coassiali possono risolvere numerosi problemi tipici delle molle singole.
Utilizzando infatti una molla singola, e non avendo particolari esigenze relative agli ingombri interni, tutto lo spazio contenuto dall’avvolgimento risulta inutilizzato. La
produzione di una molla con diametro di filo più piccolo inoltre permette di risparmiare
in fase di produzione: è sicuramente più semplice piegare un filo di diametro minore, e le barre di grande diametro sono generalmente reperibili in lunghezze limitate.
In generale i vantaggi sono quindi:
– spazio (volume) meglio utilizzato;
– lunghezze potenzialmente ridotte;
– pesi più concentrati;
– maggiore facilità di produzione.
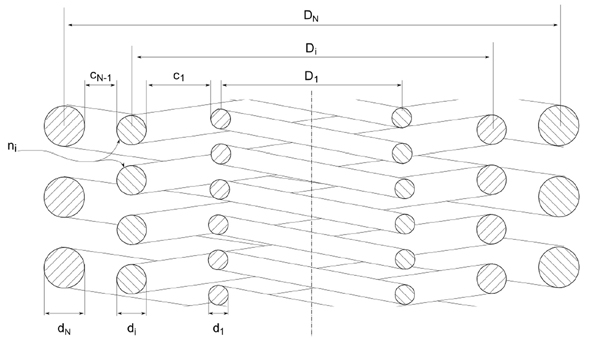
Facendo riferimento allo schema del pacco di N molle riportato in Figura 2, le molle sono separate da una distanza c che serve a evitare che disallineamenti del carico
o svergolamenti portino le molle a toccarsi.
Inoltre durante il carico il diametro della molla tende ad aumentare, seppur di poco.
Le molle sono avvolte in senso opposto, in modo da evitare che, in caso di contatto, le spire di due molle adiacenti si incastrino.
Lo schema di calcolo fa riferimento alla schematizzazione delle molle come parallelo: infatti tutte le molle costituenti il pacco subiscono la stessa deflessione e si suddividono il carico totale applicato. Proprio su questa suddivisione si baseranno tutte le successive riflessioni.
Impostando le equazioni risolutive del pacco di N molle, ci si ritrova purtroppo in un problema fortemente sottodeterminato (ci sono poche equazioni e troppe incognite).
Il problema si risolve imponendo la tolleranza fra i due diametri successivi delle molle (diametro interno della molla esterna e diametro esterno della molla interna).
Questo nell’obbiettivo di minimizzare la lunghezza del gruppo di molle: la molla più corta è quella con il diametro maggiore, ma la molla interna non può essere più grande della molla interna. Da qui la necessità di utilizzare le equazioni (1) e (2) e non la generica progettazione a partire dal diametro medio di avvolgimento.
Si impone poi come nota la ripartizione dei carichi fra le due molle, tramite un parametro α che verrà scelto opportunamente. L’idea in questo caso è che la ripartizione dei i carichi Pi sia nota a priori, introducendo quindi un fattore di ripartizione α = P1/P, da cui si possono immediatamente ricavare i carichi che agiscono sulle due molle P1 = α P; P2 = (1 – α) P.
In questo modo il problema si sposta sul come determinare il valore migliore di α. Il progettista impaziente potrà scegliere valori di α casuali e provare differenti soluzioni per trovare un compromesso (ricordando che è bene assegnare un carico maggiore alla molla più esterna). Il progettista meno frettoloso continuerà a leggere, e troverà alcuni valori di α ottimali nelle prossime righe.
Per un pacco di 2 molle quindi il procedimento di calcolo è:
> imporre il diametro esterno della molla più esterna;
> scegliere αω in base all’obiettivo del calcolo;
> dimensionare la molla esterna;
> dimensionare la molla interna a partire dal diametro interno della molla esterna, a meno di una tolleranza adeguata.
Tolleranza fra le molle
Come scegliere la distanza fra le molle?
Come detto in precedenza, la tolleranza fra le molle serve per evitare contatti e strisciamenti fra gli avvolgimenti di molle contigue. Nel caso di molle caricate prevalentemente in direzione assiale, lo sbandamento è dovuto al cattivo posizionamento del carico, e (da studi reperibili in letteratura) è quantificabile fra l’1% e il 3% del diametro, a seconda di quanto possa ritenersi ben distribuito il carico sulla prima spira.
Il pacco di molle risulta vantaggioso per limitare la lunghezza a pacco del sistema elastico. Un’ottimizzazione analitica è sconsigliabile, in quanto coinvolge un problema di minimo vincolato di quantità discrete (e non continue). Esponiamo quindi un approccio per pacchi di 2 molle coassiali, tenendo presente che difficilmente utilizzando più di tre molle coassiali si ottiene un miglioramento apprezzabile in termini di ingombro che possa giustificare l’aumento di complessità del sistema.
La minimizzazione della lunghezza a pacco non deve prescindere dal fatto che la lunghezza del pacco di molle è limitata dalla prima molla che va a pacco. Da qui la necessità di procedere per via numerica e non per via analitica.
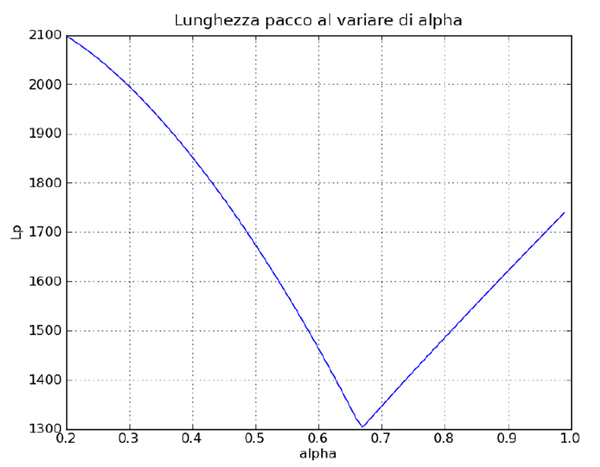
L’andamento della lunghezza a pacco reale è rappresentata (per un caso generico) in Figura 3. Si vede come sia importante scegliere un valore di α ottimale: la curva Lp(α) è molto ripida nell’intorno del minimo e, nel caso specifico, una scelta di un valore generico (0.6) porterebbe ad un aumento di Lp di 150mm (circa il 10%).
Da calcoli numerici, i parametri che influenzano la scelta di ALFA sono:
– il carico P;
– la rigidezza k;
– il diametro D;
– la tolleranza c fra le molle;
– lo sforzo tangenziale T.
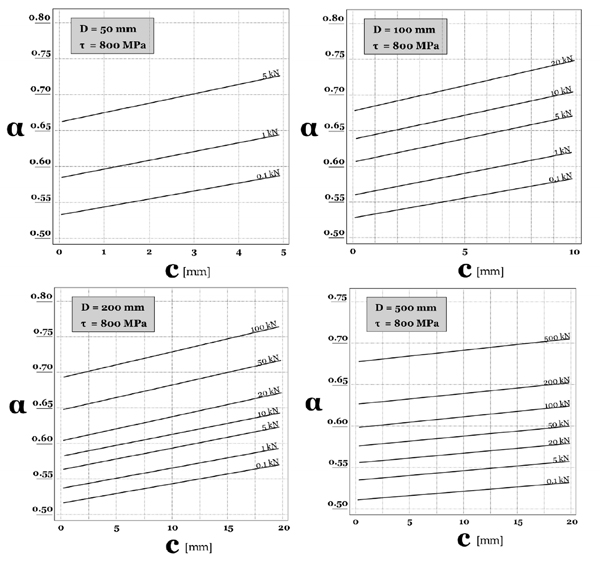
Dai diagrammi in Figura 4 si possono quindi ricavare i valori di α ottimali per il pacco di due molle.
Oltre ai vantaggi già presentati della soluzione con molle coassiali si nota anche una riduzione dell’effetto di sovrasollecitazione dovuto alla curvatura del filo, che fa si che lo sforzo sia superiore a quello calcolato nominalmente. Questo effetto è presentato in Figura 5.
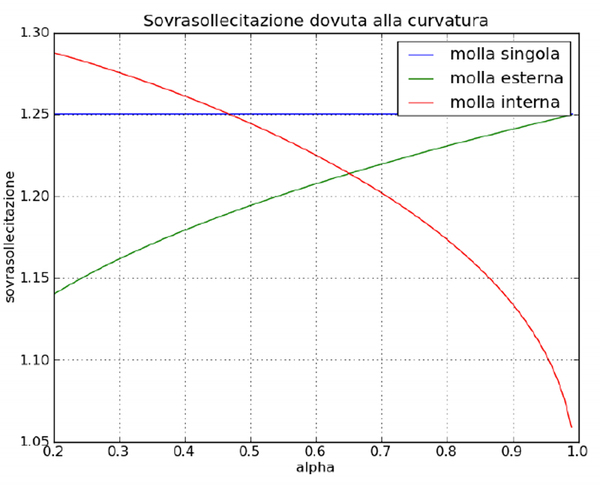
Questa diminuzione è dovuta sostanzialmente alla diminuzione del diametro del filo della molla più esterna a fronte di un aumento del diametro medio di avvolgimento, perché di fatto questa risulta meno carica della molla singola originale.
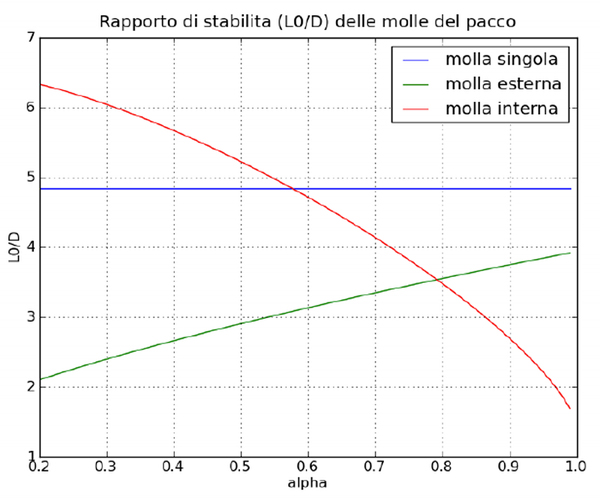
Importante è anche valutare se l’utilizzo di molle coassiali abbia o meno influenza sull’insorgere di fenomeni di instabilità. La molla esterna avrà sempre un rapporto L0/D minore rispetto alla molla singola, in quanto, se il diametro medio dell’avvolgimento varia di poco, la lunghezza a pacco diminuisce e quindi anche la lunghezza della molla libera diminuisce. È appunto questo rapporto che governa l’insorgere di instabilità: per la molla esterna non c’è problema.
Per quanto riguarda la molla interna, si possono verificare problemi di eccessiva snellezza.
In Figura 6 è rappresentato il rapporto di snellezza in funzione di α. Si vede in generale che in ogni caso, nell’intorno del valore di α ottimale, la snellezza della molla interna non supera quella della molla singola originale. Anche la stabilità è quindi migliorata.