L’estensione della vita dei recipienti in pressione

I recipienti in pressione rappresentano una delle più tipiche applicazioni con cui si devono cimentare i progettisti meccanici. Tra i problemi legati alla loro progettazione, la valutazione dell’estensione della vita operativa dei sistemi operanti ad alta temperatura rappresenta un obiettivo non facile, che sta assumendo una sempre maggiore importanza. Dopo un’introduzione relativa ai fenomeni di danneggiamento da considerare per sviluppare valutazione di questo tipo, si descrivono i procedimenti di verifica considerati dalle norme e i requisiti da queste richiesti

Mario Guagliano – Dipartimento di Meccanica, Politecnico di Milano

È sempre più frequente la richiesta di estendere la vita operativa dei sistemi in pressione (e non solo di questi) oltre a quella prevista in sede di progetto, in modo da rimandare la loro sostituzione nel tempo. Decisioni di questo tipo si basano su considerazioni ingegneristiche che devono tenere in conto le effettive condizioni di esercizio durante tutta la vita operativa del sistema e il loro confronto con quanto previsto in sede di progetto, i materiali utilizzati e i requisiti richiesti dalle norme per esprimere un giudizio e per quantificare l’eventuale estensione della durata in esercizio.
Inoltre, il tecnico incaricato di valutazioni di questo tipo deve, per prima cosa, conoscere quali sono i meccanismi di danneggiamento legati alle condizioni di esercizio del sistema (temperatura, carichi applicati, loro variabilità nel tempo) e le equazioni che ne descrivono l’evoluzione nel tempo. Due, in particolare, sono i tipi di danneggiamento più comuni in tali condizioni: il creep, o scorrimento viscoso, e la fatica. Il primo è legato alla temperatura di esercizio e si manifesta quando questa raggiunge valori superiori a circa metà della temperatura di progetto espressa in Kelvin. La fatica è, invece, legata alla variabilità ciclica dei carichi applicati ed è stata oggetto di recenti contributi su queste colonne.
Dopo un’introduzione in cui si descrivono le caratteristiche del creep, si focalizza l’attenzione sulle metodologie più comuni per questo tipo di valutazioni relative ai sistemi in pressione operanti ad elevata temperatura e, in particolare, sulle norme che dettano le modalità di valutazione della vita residua di un sistema.

Il creep
Quando un materiale è sollecitato a temperatura elevata rispetto a quella di fusione (come si diceva prima superiore a metà di quest’ultima, se espressa in Kelvin) le deformazioni associate a carichi costanti aumentano nel tempo, e possono assumere valori pericolosi per la funzionalità del sistema e, anche, per la sua integrità strutturale. Il fenomeno si sviluppa nel tempo in modo diverso a seconda della severità dello stato di sforzo e della temperatura di esercizio, ma può essere descritto definendo fasi caratterizzate da una dinamica differente. Tali fasi sono qualitativamente illustrate in Figura 2, in cui si mostra un grafico in cui, in ascissa, compare il tempo e in ordinata la deformazione accumulata.
Si notano tre differenti periodi: il primo, indicato come “creep primario”, comincia appena dopo l’applicazione del carico ed è caratterizzato da una velocità di deformazione decrescente. Il secondo, detto creep secondario, presenta una velocità di deformazione costante nel tempo e si protrae fino all’inizio della terza fase, creep terziario, che porta alla rottura del pezzo. A seconda delle condizioni di esercizio le tre fasi possono tutte manifestarsi oppure no. Se la temperatura e lo stato di sforzo sono adeguatamente bassi, il creep si può esaurire con la fase primaria e la deformazione tendere a un valore stabile dopo un certo periodo di tempo.
Di queste tre fasi quella che più interessa la valutazione della vita residua di un sistema in pressione è il creep secondario, in quanto è quella che occupa la maggior parte della durata di esercizio dei sistemi in pressione, rendendo quantitativamente trascurabili le altre due fasi. Questa fase è matematicamente decritta dalla legge del Norton, secondo la quale

dε/dt=kσⁿ

dove dε/dt è la velocità di deformazione, σ lo sforzo applicato e k e n un coefficiente e un esponente che dipendono dal materiale e dalla temperatura che vengono ricavati con prove sperimentali.
E’ facile intuire che lo sviluppo di prove organizzate a tal fine è molto oneroso in termini economici ma lo è, ancor più, pensando ai tempi necessari per ottenere dei dati utili. I sistemi in pressione soggetti a valutazioni sulla loro vita residua sono tipicamente sollecitati da sforzi relativamente bassi per periodi molto lunghi, mentre la caratterizzazione dei materiali al creep è condotta con prove con sforzi applicati elevati; il che dà luogo a tempi di rottura molto minori. Il problema, quindi, è definire un metodo per mettere in relazione i risultati delle prove con le condizioni operative del recipiente ed eseguire la verifica dello stesso.
A tal fine sono stati messi a punto i metodi parametrici, che si basano sulla definizione di parametri sintetici che tengano conto delle grandezze che influenzano lo sviluppo del creep e permettano di utilizzare dati relativi a determinate condizioni di prova per verifiche relative ad impianti operanti in situazioni differenti.
Diversi sono i parametri che sono stati proposti a tal fine nel corso degli anni; tra questi, quello proposto da Larson e Miller ha avuto la maggiore fortuna ed è adottato oggi in molte codici per la valutazione dell’estensione della vita operativa di un sistema.

Il parametro di Larson e Miller (P_LM) e la procedura tecnica ISPESL
Il parametro di Larson e Milller è stato proposto nella seconda metà del secolo scorso e si basa sull’ipotesi che il fenomeno del creep si attivi seguendo legge una legge del tipo di Arrhenius e che l’energia di attivazione sia funzione del solo sforzo. Si ipotizza, inoltre, che il prodotto tra il tempo di rottura e la velocità di deformazione sia costante, il che vuol dire che la deformazione di rottura non varia al variare delle condizioni di temperatura e sforzo. Con alcuni passaggi matematici si arriva alla definizione del parametro, come:
P_LM=f(σ)=T(C+log₁₀t_R)
in cui T è la temperatura assoluta, tR è il tempo di rottura e C una costante funzione del materiale. Nella formula si nota anche che il parametro di Larson è Miller è funzione del solo valore dello sforzo applicato (f(σ)). Grazie a questa formulazione è possibile determinare C eseguendo prove con il medesimo valore di sforzo applicato a temperature differenti: si può, infatti, notare che se si traccia un grafico in cui si pone log10tR in ascissa e 1/T in ordinata si ottiene un andamento lineare e che C può essere determinata come l’intersezione di questa retta con l’asse delle ascisse.
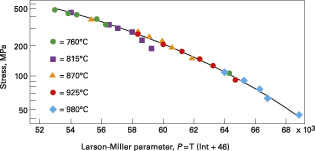
L’applicazione del metodo richiede che si traccino le curve che legano lo sforzo applicato al PLM (vedi Figura 3) e che, noto lo sforzo d’interesse, si calcoli il corrispondente valore del parametro di Larson e Miller.
Noto questo e la temperatura di esercizio, si può stimare il tempo atteso di rottura e confrontarlo con quello stimato in sede di progetto. In tal modo si procede con la stima della vita residua e si valuta l’opportunità di estendere l’utilizzo del sistema oltre la scadenza fissata inizialmente.

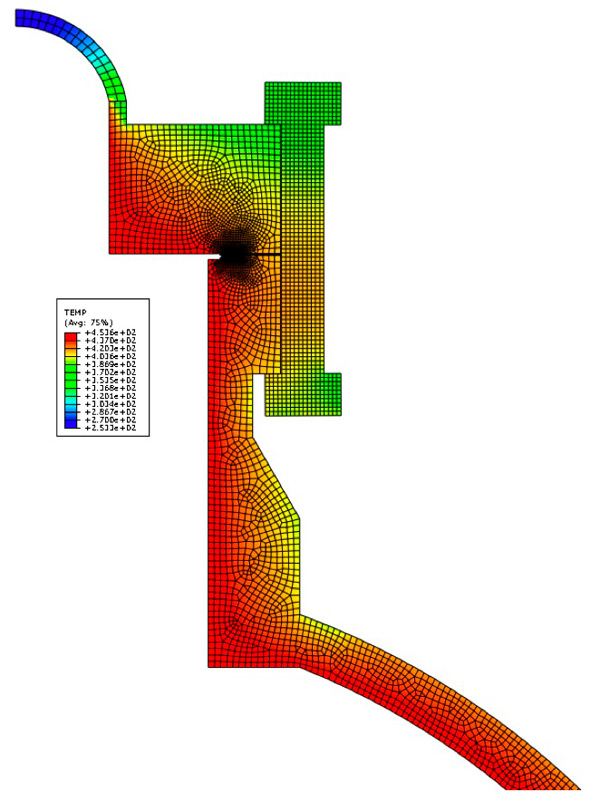
Il metodo è stato implementato in diversi codici riguardanti il progetto dei sistemi in pressione, i quali, tuttavia, evidenziano anche i limiti operativi del metodo. Ad esempio la procedura tecnica ISPESL sull’estensione della vita dei recipienti in pressione mette in guardia relativamente al corretto utilizzo del parametro. E’ noto, infatti, che, a seconda delle coppie di valori di temperatura e di sforzo applicato, lo scorrimento viscoso si manifesta attivando differenti meccanismi microstrutturali di deformazione. Ciò rende problematica una corretta estrapolazione dei dati relativi a condizioni di prova e di esercizio differenti, limitando, di fatto, l’utilizzo del parametro a condizioni di prova che coinvolgano i medesimi meccanismi di danno. Il documento ISPESL segnala il problema ed impone dei limita all’estrapolazione a 3 per quanto riguarda i tempi e di un ordine di grandezza per il calcolo della vita teorica totale. La procedura suggerisce, in casi differenti, di ricorrere alle cosiddette mappe di Asbhy (che danno la mappa dei meccanismi di scorrimento viscoso in funzione di sforzo e temperatura) per estrapolazioni maggiori.
Il calcolo del danneggiamento è eseguito mettendo a rapporto il tempo effettivamente speso in assegnate condizioni e quello che, alle stesse condizioni, porta alla rottura.
Se il sistema ha operato in condizioni di temperatura e sforzo diverse, si ripete il procedimento per ogni situazione di esercizio e si sommano i rapporti tempo effettivo/tempo di rottura relativo ad ogni periodo: tale sommatoria deve risultare, per dare esito positivo, minore dell’unità. Se oltre al creep si verificano anche cicli di fatica è necessario sommare anche questo danno a quello del creep utilizzando la legge di Miner e verificando, ancora, che il danno totale sia inferiore a 1.

Il metodo MPC-Ω e il Code Case ASME 2605
Ai metodi parametrici per la valutazione della vita residua si è recentemente aggiunto, da un punto di vista applicativo, il metodo MPC-Ω, sviluppato da Prager negli anni novanta del secolo scorso e ripreso da Code Case 2605 dell’ASME per la valutazione della vita residua di sistemi eserciti e costruiti con alcune ben definite categorie di acciai.
Il metodo si basa sui concetti della meccanica del danneggiamento del continuo (CDM) e parte dal principio di equivalenza di Lemaitre, secondo il quale il comportamento a deformazione di un materiale danneggiato può essere descritta da equazioni costitutive del materiale non danneggiato in cui allo sforzo convenzionalmente definito si sostituisce lo sforzo effettivo. L’ipotesi innovativa introdotta nel metodo è che il danno, durante il creep terziario, sia scomponibile in due componenti mediante funzioni esponenziali a loro volta riconducibili al parametro Ω_p, con

Ω_p=m+p+c

in cui
•m rappresenta l’aumento di sforzo effettivo previsto dalla legge di Norton;
•p tiene conto del danno microstrutturale;
•c di altri fattori microstrutturali dovuti al cambio delle sollecitazioni e a deficienze nella stima di m.

Questo coefficiente descrive effettivamente quanto il materiale degradato sia in grado di resistere agli sforzi applicati. Ω_p è funzione dello sforzo, della temperatura e del tipo di carico applicato, può essere rappresentato in forma parametrica ed è utile per valutare la vita residua e il danno accumulato.
Attraverso questo metodo si dimostra che il tempo di rottura e le deformazioni accumulate sono le conseguenze di una velocità della deformazione e del valore Ωp relativo alle condizioni operative e alla geometria di interesse.
Tra i vantaggi del metodo vi sono la facilità con cui possono essere calcolati la deformazione accumulata, quella successiva, la velocità di deformazione corrente e la durata residua del sistema. Inoltre il metodo ben si presta all’implementazione in calcoli a elementi finiti attraverso lo sviluppo di subroutine a cura dell’analista.

Bibliografia

Jawad, H.J. Farr, J.R., Structural Analysis and Design of Process Equipment, John Wiley & Sons, 1988.
J. Spence, A.S. Tooth, Pressure Vessel Design, E&F N SPON, 1994.
M. Prager, Development of the MPC Omega Method for Life Assessment in the Creep Range, J. Pressure Vessel Technol. Vol. 117, 2005,
Anonimo, Procedura Tecnica su: Verifiche di calcolo e controlli su componenti in pressione in regime di scorrimento viscoso del materiale, ISPESL, 2003.
Anonimo, ASME Section VIII, Division 2, Code Case 2605, 2007.