La progettazione dei meccanismi cedevoli

I meccanismi cedevoli sono sempre più frequentemente impiegati in numerosi settori della tecnica per una serie di vantaggi competitivi, tra cui i bassi costi, facilità di montaggio e una migliore realizzabilità. Vediamo quali sono le metodologie di progettazione

Pier Paolo Valentini
Un meccanismo cedevole è un dispositivo meccanico impiegato per la trasmissione di movimento, forze o energia in maniera del tutto analoga ad un meccanismo composto interamente da corpi rigidi. Le differenze con quest’ultimo risiedono, però, nel fatto che un meccanismo cedevole ottiene la sua mobilità grazie alla deformazione di membri e componenti flessibili anziché mediante l’impiego di specifiche coppie cinematiche (guide, cerniere, coppie sferiche, etc.). A rigore, pertanto, un meccanismo cedevole non possiede gradi di libertà in senso stretto, ma preserva comunque la possibilità di articolazione grazie alla deformazione delle sue parti.
La principale sfida nelle attività di progettazione dei meccanismi cedevoli riguarda quindi una attenta definizione delle proprietà morfologiche e strutturali affinché nella deformazione il meccanismo cedevole realizzi un’articolazione voluta e controllata nel rispetto della funzionalità richiesta.
I meccanismi cedevoli sono sempre più frequentemente impiegati in numerosi settori della tecnica per una serie di vantaggi competitivi. Innanzitutto sono dispositivi generalmente a basso costo, di facile realizzazione e facili da montare. Possono essere realizzati mediante comuni stampaggi di materiale plastico o mediante tagli di lamiere. In secondo luogo, permettono elevate prestazioni in termini di precisione, affidabilità, bassa usura, peso ridotto, elevata silenziosità e bassissima manutenzione. Tutte queste caratteristiche li rendono particolarmente adatti per l’impiego in sistemi miniaturizzati (MEMS – Micro Electro-Mechanical Systems) e in applicazioni destinate ad ambienti particolari o ostili (settore aeronautico, aerospaziale, etc.).
Alcuni esempi di meccanismi cedevoli sono illustrati in Figura 1.

Dal momento che la mobilità e l’articolazione dei meccanismi cedevoli si basa sulla presenza di parti flessibili che deformandosi immagazzinano energia, è possibile sfruttare nella loro progettazione la presenza di elementi elastici distribuiti, senza dover necessariamente inserire dei componenti specifici come le molle. Questa caratteristica da un lato permette una maggiore flessibilità nella progettazione e semplicità costruttiva, ma da un altro complica le attività di sintesi ed analisi richiedendo un approccio integrato tra cinematica, meccanica strutturale e dinamica. La mobilità dei meccanismi cedevoli, infatti, è permessa grazie alle deformazioni dei relativi membri che dovranno tuttavia essere limitate da considerazioni resistenziali, causando di conseguenza limitazioni sugli spostamenti relativi ammissibili per la struttura. Inoltre, la presenza di carichi variabili e ripetitivi impone di tenere spesso ulteriormente in conto aspetti di fatica.
Per questi motivi, progettare meccanismi cedevoli non è un compito agevole, ma richiede lo sviluppo e l’impiego di metodologie alquanto più complesse rispetto a quelle impiegate per i meccanismi con soli corpi rigidi. In passato i meccanismi cedevoli venivano progettati e dimensionati mediante approcci try and error con notevole dispendio di tempo, risorse e costi non trascurabili e soprattutto senza la possibilità di acquisire conoscenze specifiche o sviluppare metodologie generali.
Lo scopo di questo quaderno di progettazione è appunto quello di illustrare alcune metodiche sistematiche attualmente impiegate nella pratica ingegneristica per affrontare la progettazione di una larga classe di meccanismi cedevoli.
Come per tutte le classi di meccanismi (sia rigidi, sia cedevoli) è possibile distinguere nella progettazione le metodiche di analisi, adatte per uno studio approfondito di meccanismi già dimensionati e metodiche di sintesi, destinate a dimensionare nuovi meccanismi a partire dalla loro prevista funzione.
Nelle metodologie di progettazione specifiche dei meccanismi cedevoli, sia nelle attività di analisi, sia in quelle di sintesi assume grande rilievo il concetto di meccanismo pseudo rigido equivalente. Esso è rappresentato da un meccanismo a corpi rigidi e rigidezze concentrate che riproduce in maniera più accurata possibile il funzionamento del meccanismo cedevole ad esso associato sia in termini cinematici sia in termini dinamici. Il meccanismo pseudo rigido permette pertanto, entro limiti di approssimazione, l’applicazione delle comuni tecniche di analisi e sintesi tipiche dei generici meccanismi a corpi rigidi, con la possibilità di trasferire i risultati adattandoli alla presenza di elementi flessibili.
La definizione di un meccanismo pseudo rigido permette un approccio rapido e sufficientemente accurato per semplificare le complesse relazioni di forze-spostamenti all’interno dei membri flessibili del meccanismo cedevole e ne permette una precisa stima dei campi di spostamento e delle reazioni elastiche corrispondenti. Dalla conoscenza degli spostamenti sarà poi possibile dal confronto tra il meccanismo pseudo-rigido e cedevole, calcolare le deformazioni e le tensioni all’interno dei componenti per poi procedere all’analisi di resistenza per trarre utili informazioni ai fini della progettazione e dell’ottimizzazione strutturale.
Data l’estrema variabilità delle soluzioni possibili nella progettazione creativa dei meccanismi cedevoli, anche la corrispondente definizione degli equivalenti meccanismi pseudo rigidi risulta estremamente vasta.
In questo quaderno ci soffermeremo con l’analizzare le può comuni soluzioni che possono essere impiegate e per ciascuna dedurremo il corrispondente meccanismo pseudo rigido. Quando si procederà alla progettazione di meccanismi più complessi, per ciascun elemento flessibile sarà compito del progettista individuare il corrispondente meccanismo pseudo rigido e quindi definire il meccanismo pseudo rigido equivalente dell’intera struttura cinematica mediante composizione.
Il punto chiave nella definizione dei meccanismi pseudo rigidi è la scelta del posizionamento delle coppie cinematiche e dei relativi elementi elastici che ne riproducano gli effetti di cedevolezza. Nei meccanismi cedevoli, infatti, gli elementi flessibili incorrono praticamente sempre in grandi spostamenti. Tali deformazioni sono necessarie proprio per garantire l’articolazione del meccanismo e quindi la sua mobilità. Questa caratteristica comporta tuttavia una complicazione nelle formulazioni matematiche per il calcolo delle rigidezze equivalenti con l’introduzione di un evidente effetto di non linearità geometrica. Fortunatamente, nella maggior parte dei casi, i materiali impiegati permettono ancora di considerare un legame lineare tra tensioni e deformazioni e quindi l’applicazione con adeguata precisione della legge di Hooke.
Analizziamo ora le principali strutture base per la costruzione di meccanismi pseudo-rigidi equivalenti.

Cerniere flessibili con segmenti di piccola lunghezza
In molte implementazioni dei meccanismi cedevoli, è possibile realizzare una cerniera flessibile andando a sagomare opportunamente un geometria di un membro assottigliandola in corrispondenza di un breve tratto. Così facendo è possibile ottenere un comportamento flessionale localizzato, permettendo, grazie alla deformazione, la rotazione relativa dei membri collegati, realizzando di fatto il comportamento di una cerniera. Con riferimento alla Figura 2, è possibile notare una trave la cui estremità è assottigliata per una lunghezza molto limitata e quindi incastrata mediante un supporto.

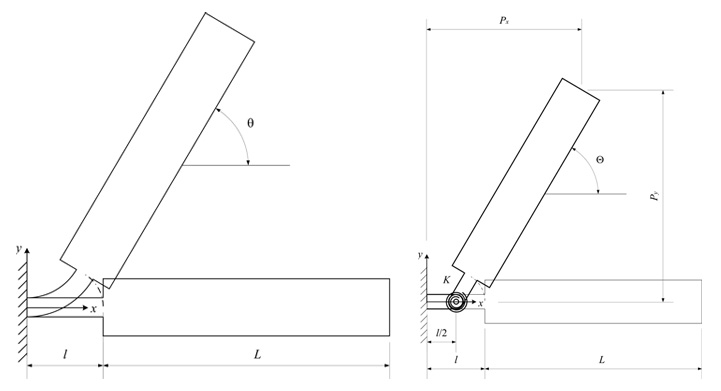
È abbastanza intuitivo notare che la trave ha una parte di lunghezza L sufficientemente rigida e una di lunghezza l decisamente più flessibile.  Nella pratica progettuale la lunghezza l è circa 1/10 della lunghezza L della porzione più rigida al fine di consentire una corretta localizzazione del centro di rotazione.
Una tale soluzione può essere studiata ricorrendo al modello pseudo rigido di Figura 2 nel quale è stata inserita una cerniera in mezzeria dell’estremità assottigliata congiuntamente con una molla torsionale. Sotto l’ipotesi di piccola lunghezza l l’angolo di flessione della porzione rigida Θ può considerarsi uguale a quello del membro rigido Θ.
La rigidezza lineare K della molla torsionale da includere nel modello pseudo rigido può essere calcolata a partire da relazioni strutturali e risulta essere:

È opportuno sottolineare che l’approssimazione del modello pseudo rigido risulta essere tanto più accurata quanto:
sono presenti solo azioni flessionali, ovvero sono limitati gli sforzi normali o trasversali che tenderebbero a allungare/accorciare la trave;
la porzione assottigliata è di limitata lunghezza, così da non introdurre non linearità nella sua deflessione.
In una cerniera flessibile di piccola lunghezza la sollecitazione massima si misura in corrispondenza della sezione incastrata del segmento assottigliato. È proprio lì che dovrà essere eseguita la verifica di resistenza. Considerando il solo contributo del momento flettente, considerando un momento di reazione della sezione incastrata pari a M_f  la tensione massima σ_max potrà calcolarsi come:

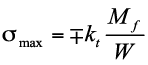
dove:
W  è il modulo di resistenza a flessione;
k_t è il fattore di concentrazione delle tensioni dovuto alla brusca variazione di dimensioni della sezione resistente che andrà calcolato in funzione delle specifiche condizioni geometriche.

Segmenti interamente flessibili
In molti casi la flessibilità e quindi il movimento della struttura si ottiene grazie alla deformazione di un intero segmento flessibile (Figura 3). Al contrario del caso delle cerniere flessibili a piccola lunghezza nelle quali la deformazione flessionale è concentrata in una sola porzione della struttura, la deformazione interesserà l’intero segmento.

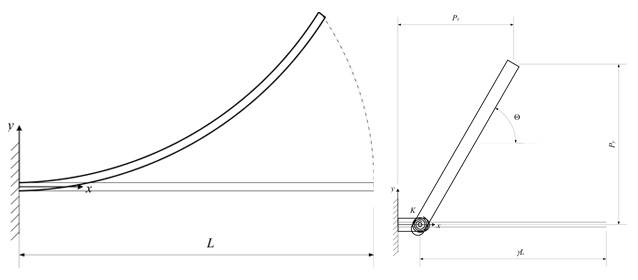
In termini rigorosi, l’accurata stima della deformazione di un segmento incastrato soggetto ad una forza in corrispondenza di una sua estremità richiede un impianto matematico di non poca complessità. Anche in questo caso, però, una approssimazione lineare della deformazione porta alla definizione di un modello pseudo rigido sufficientemente accurato per un buon dimensionamento.
In queste condizioni è possibile costruire un modello pseudo-rigido caratterizzato da due corpi rigidi connessi da una cerniera ed un elemento elastico torsionale che preservi la rigidezza flessionale del sistema (Figura 3).  Per comodità la posizione d della coppia cinematica può essere espressa in termini della lunghezza complessiva L della trave e del raggio caratteristico γ come:
d=γ L
Il valore del rapporto di raggio caratteristico γ dipende da diversi fattori, tra cui le condizioni di carico. È tuttavia possibile considerare un valore medio, adatto praticamente alla totalità delle situazioni progettuali, pari a γ_medio=0.85 .
Il coefficiente di rigidezza K della molla torsionale da associare alla cerniera, ha dipendenza dalle caratteristiche geometriche e resistenti della trave, nonché da un fattore di rigidezza torsionale K_Θ:

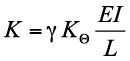
dove:
E è il Modulo di Young del Materiale;
I  è il momento di Inerzia della sezione resistente nella direzione di flessione.
Anche per il fattore di rigidezza torsionale K_Θ è possibile adottare un valore medio, adatto a molteplici scenari progettuali pari a K_Θmedio = 2.56 .
In un segmento interamente flessibile incastrato la sollecitazione massima si misura in corrispondenza della sezione inamovibile. È proprio lì che dovrà essere eseguita la verifica di resistenza. Considerando il solo contributo del momento flettente, considerando un momento di reazione della sezione incastrata pari a M_f , la tensione massima σ_max potrà calcolarsi come:

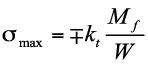
dove:
W è il modulo di resistenza a flessione;
k_t è il fattore di concentrazione delle tensioni dovuto alla brusca variazione di dimensioni della sezione resistente che andrà calcolato in funzione delle specifiche condizioni geometriche.

Segmenti flessibili con incastro e guida lineare
In molti azionamenti e controlli è frequente trovare delle soluzioni che prevedano la schematizzazione di un componente mediante un segmento flessibile con entrambe le estremità incastrate, ma una delle due cedevole e soggetta ad uno spostamento imposto (Figura 4).
In questa configurazione il modello pseudo rigido che può essere impiegato è illustrato in Figura 4. Si tratta di un sistema a 3 corpi rigidi e due cerniere con le relative molle torsionali per preservare la componente elastica della soluzione.

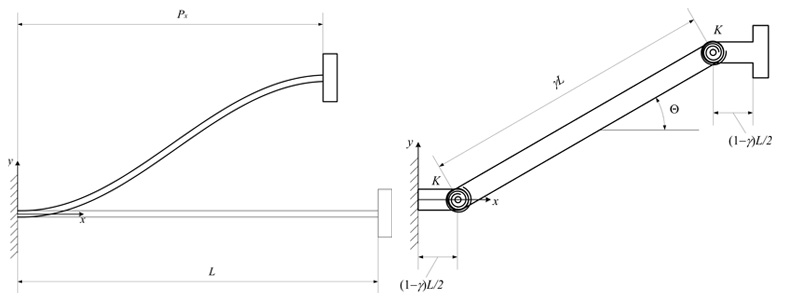
Da un punto di vista matematico, lo studio di un segmento flessibile con incastro e guida lineare si può ricondurre ad un semplice segmento flessibile con estremità libera soggetto ad una forza a patto di considerare una trave di lunghezza L/2.
Seguendo il medesimo approccio illustrato in precedenza e considerando le approssimazioni introdotte, avremo, per un segmento flessibile con incastro e guida lineare un valore del rapporto di raggio caratteristico pari a: γ = 0.8517
È possibile calcolare le costanti elastiche delle due molle torsionali come:
k_t = k₂ = 2γ k_Θ EI-L
ella quale il coefficiente k_Θ può essere approssimato sempre con un valore medio pari a k_Θmedio = 2.65.
È facile notare che essendoci molle in parallelo ed essendo ciascuna molla doppiamente rigida rispetto al semplice casi di segmento interamente flessibile con estremità rigida, la soluzione di segmento flessibile con incastro e guida lineare è complessivamente quattro volte più rigida.
In un segmento flessibile con incastro e guida lineare la sollecitazione massima si misura in corrispondenza di entrambe le sezioni incastrate dove è massimo il momento flettente. È proprio lì che dovrà essere eseguita la verifica di resistenza. Considerando, anche in questo caso, il solo contributo del momento flettente, considerando un momento di reazione della sezione incastrata pari a M_f, la tensione massima σ_max potrà calcolarsi come:

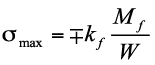
dove:
W è il modulo di resistenza a flessione della sezione.
k_t è il fattore di concentrazione delle tensioni dovuto alla brusca variazione di dimensioni della sezione resistente.

Cerniere concentrate
Le cerniere concentrate sono un particolare caso di cerniere flessibili con segmenti di piccola lunghezza. Sono realizzate grazie ad un restringimento molto accentuato e ad una limitata lunghezza che conferisce loro una bassissima rigidezza, realizzando approssimativamente una accoppiamento rotoidale senza resistenza elastica.
Le cerniere concentrate, vista la facilità di realizzazione e le loro notevoli proprietà cinematiche, possono ritrovarsi in una vasta casistica di prodotti sul mercato. Generalmente, il materiale più utilizzato per gli elementi con cerniere concentrate è il polipropilene, poiché offre un ottimo comportamento a fatica, permettendo una lunga vita ai componenti.
La costruzione di un modello pseudo rigido di una cerniera concentrata prevede esclusivamente l’implementazione di una coppia rotoidale in corrispondenza della cerniera stessa, senza l’aggiunta di una molla torsionale.

Un esempio di analisi
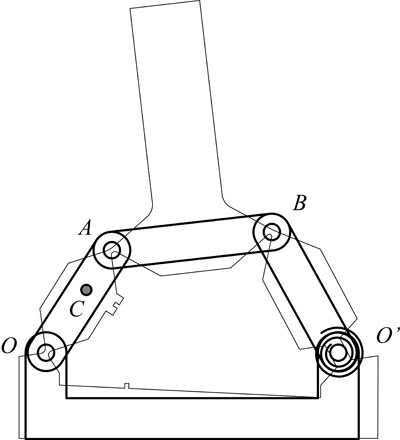
Per illustrare le potenzialità dell’approccio alla progettazione dei meccanismi cedevoli mediante l’impiego dei modelli pseudo rigidi, affrontiamo un problema di dimensionamento di un interruttore bistabile. Il sistema illustrato in Figura 5 è composto da un unico elemento flessibile che presenta tre cerniere concentrate e un segmento flessibile di piccola lunghezza. La funzione dell’intero componente è quella di permettere, mediante l’azione di una forza in corrispondenza del risalto centrale, la rotazione di un elemento per ottenere la chiusura stabile di alcuni contatti. Il sistema è definito bistabile perché è possibile mantenere sia la configurazione di contatti aperti, sia quella di contatti chiusi senza l’applicazione di forze esterne, ma solo grazie all’immagazzinamento di energia elastica interna durante la fase di articolazione. La forza esterna è pertanto necessaria solo per il passaggio da una configurazione stabile all’altra.

Lo scopo del dimensionamento proposto come esempio è quello di scegliere la geometria del segmento flessibile di piccola lunghezza affinché la forza di chiusura dei contatti sia almeno pari ad un valore F_contatto = 5 _N di specifica. Sotto queste condizioni si vuole anche conoscere il valore della forza massima necessaria a chiudere il contatto.
Il primo passo è quello di costruire un modello pseudo-rigido del dispositivo. È facile verificare, in base alle considerazioni precedenti che il sistema può essere assimilato ad un quadrilatero articolato con tre cerniere libere (in corrispondenza degli assottigliamenti concentrati e una controllata da una molla torsionale in corrispondenza del segmento flessibile (Figura 6).

I dati dimensionali del problema sono illustrati in Tabella 1.

Tabella 1. Parametri geometrici dell’interruttore bistabile

Grazie a questa trasposizione, il sistema può essere studiato come un comune meccanismo a corpi rigidi. In particolare, i valori degli angoli di rotazione delle aste rispetto al telaio possono essere calcolati mediante le equazioni vettoriali di chiusura o anche per via grafica (Figura 7).
I valori angolari delle due configurazioni stabili sono riportati in Tabella 2. Imponendo geometricamente l’allineamento delle cerniere  O, A e B, è possibile calcolare i valori degli angoli di rotazione delle aste in corrispondenza della configurazione critica necessaria per realizzare la seconda posizione stabile (Figura 7). Tali valori sono anch’essi riportati in Tabella 3.

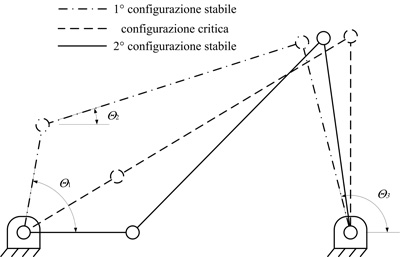
Tabella 2. Angoli di rotazione delle aste rispetto al telaio per le differenti configurazioni

Il valore della forza che assicura la chiusura dei contatti può essere determinato mediante l’applicazione dei principio dei lavori virtuali:

dove:
K è la rigidezza della molla equivalente in corrispondenza della cerniera;
F_contatto è la forza di chiusura dei contatti;
δΘ_{3_stabile2} è lo spostamento virtuale infinitesimo di rotazione della cerniera tra il terzo membro e il telaio nella seconda configurazione stabile (contatti chiusi);
δS_{C_stabile2} è lo spostamento virtuale infinitesimo del punto di riferimento C dei contatti nella seconda configurazione stabile (contatti chiusi).
Per risolvere la  è possibile utilizzare la relazione:

La relazione che lega gli spostamenti infinitesimi angolari δΘ_{1_stabile2} δΘ_{3_stabile2}
può essere trovata osservando che nella seconda configurazione stabile, il punto C è anche il centro di istantanea rotazione del moto relativo tra la prima e la terza asta. Per questo motivo è possibile scrivere:

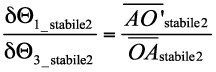
Adesso è possibile tornare all’Equazione   e sostituire la  e la, ottenendo la costante di rigidezza K:
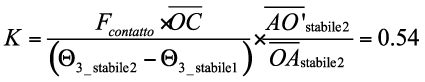Nm/rad
Mediante l’applicazione della  è possibile calcolare le proprietà geometriche del segmento flessibile. Supponendo noto il materiale (lo stesso del resto del componente) rimane da scegliere la sezione e la lunghezza del segmento. Nel caso di sezione quadrata di lato b potremo scrivere:

La  lascia ampia scelta nella definizione dei parametri l e b. Tale dimensionamento deve essere eseguito nel rispetto dei requisiti di resistenza, ovvero imponendo che lo sforzo massimo sia inferiore a quello ammissibile (tenendo conto degli eventuali fenomeni di fatica e delle concentrazioni di tensione dovute alle singolarità geometriche). Imponendo una lunghezza l = 0.1xBO, e scegliendo come materiale il nylon con modulo di Young E = 1000 MPa otteniamo:
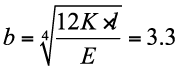mm
È possibile dunque calcolare il momento flettente massimo agente sulla cerniera elastica, che si verifica nella configurazione di massima deformazione che è la configurazione critica come:
N
e, di conseguenza, supponendo un valore del fattore di concentrazione delle tensioni pari a K_f = 1.2, la massima tensione corrispondente:
MPa
Il valore così determinato andrà confrontato con i corrispondenti valori di resistenza del materiale (verifica statica o a fatica).