Un nuovo metodo per analizzare reti complesse che potrà essere applicata allo studio di fenomeni di estrema complessità per l’intreccio delle connessioni.
Per studiare quello che avviene o potrebbe avvenire in reti estremamente complesse, come in una pandemia o nelle interazioni su Internet, è utile semplificare il sistema per renderlo gestibile e poterlo analizzare.
Ma come si può trovare il giusto punto di osservazione per comprendere a colpo d’occhio le caratteristiche salienti del tutto senza perdere di vista connessioni rilevanti?
Semplificare le reti complesse
Un team di fisici fra cui Guido Caldarelli, autore corrispondente dello studio e professore di Fisica teorica all’Università Ca’ Foscari Venezia, ha trovato un metodo per ‘semplificare’ in modo efficiente ed efficace la struttura complessa della rete. Il risultato è stato pubblicato su Nature Physics ed è quindi a disposizione della comunità scientifica internazionale.
Gli studiosi hanno preso spunto dalla tecnica che valse il Nobel al fisico statunitense Kenneth G. Wilson nel 1982. Wilson riuscì a trovare una teoria in grado di spiegare il funzionamento delle transizioni di fase, come il congelamento della superficie di un lago o la formazione di una colonna d’auto per il traffico. Inventò la tecnica matematica del gruppo di rinormalizzazione, che consente di sfruttare una simmetria della natura (il grande è simile al piccolo) per prevedere il comportamento di alcuni sistemi.
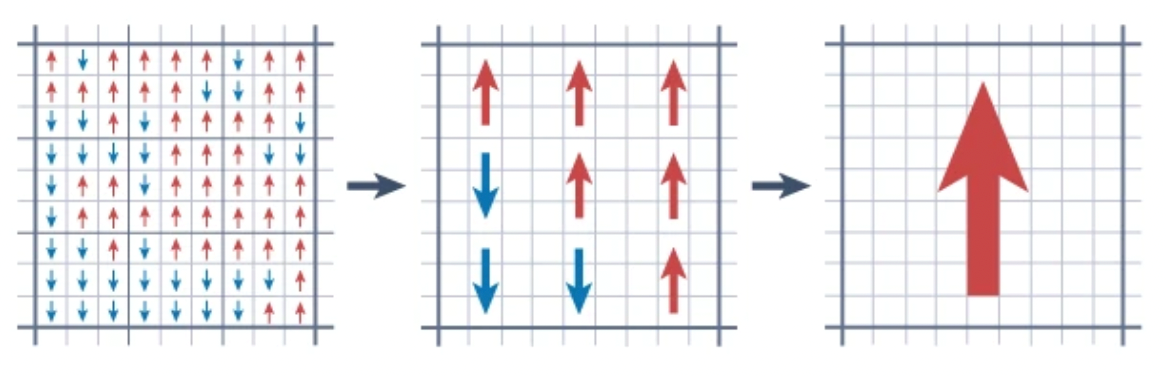
Una parte di questo metodo consiste nel riscalare le celle in cui è definito il sistema con celle sempre più grandi. Ad ogni passo si accorpano sia le celle del sistema che le variabili che compongono il sistema (come in figura dove abbiamo rappresentato un sistema di spin).
La conoscenza del sistema una volta finita la serie di accorpamenti è in grado di dirci come si comporta il sistema originario a grandi distanze e verso quali punti fissi si diriga l’evoluzione del sistema stesso.
Ma come ottenere lo stesso vantaggio quando il sistema non è costituito da celle come un foglio di calcolo, ma da nodi e relazioni tra questi come avviene nel nostro cervello con i neuroni, nel contagio tra individui infetti e suscettibili o con le interazioni sui social media?
Nei sistemi reali molto spesso, se non sempre, le interazioni sono caratterizzate dalla presenza di una complessa struttura delle connessioni che le rende molto difficili da analizzare.
“Direttamente ispirati alle idee della fisica statistica – spiega Caldarelli – abbiamo introdotto una nuova procedura di gruppo di rinormalizzazione che si è rivelata essenziale per scoprire in modo efficiente ed elegante l’organizzazione a scale multiple di reti complesse e per rilevare caratteristiche invarianti di scala quando presenti. Inoltre, definisce una procedura universale di ridimensionamento delle reti che è da un lato molto utile per l’analisi di grandi moli di dati e dall’altro lato ci mostra una delle fondamentali simmetrie della natura”.
Fra le applicazioni future su cui il team lavorerà c’è il filtraggio di moli di dati sperimentali l’esplorazione dello spazio dei materiali e la rappresentazioni di informazioni provenienti da archivi storici.
L’articolo scientifico:
Laplacian renormalization group for heterogeneous networks
Villegas, P., Gili, T., Caldarelli, G. et al. Laplacian renormalization group for heterogeneous networks. Nat. Phys. (2023). https://doi.org/10.1038/s41567-022-01866-8