Qualsiasi struttura è caratterizzata da un set di modi propri di vibrare che dipendono dalle sue caratteristiche di massa e di rigidezza (per una corretta comprensione del problema sono state riportate le equazioni per il calcolo dei moti propri di vibrare nel Riquadro 1).
L’applicazione principale dell’analisi in frequenza è il calcolo delle frequenze proprie del sistema: un’applicazione di questo tipo di calcolo (illustrata in figura 1) può essere la verifica della vibrazione di una struttura di supporto di un motore. Generalmente, per escludere effetti di amplificazione delle vibrazioni dovute alla frequenza del carico agente, si verifica che la struttura non abbia frequenze proprie coincidenti con un valore da 1 a 3 volte quello della frequenza della forzante (il carico applicato).
L’analisi in frequenza può essere utilizzata come strumento di supporto ad un’analisi statica quando il solutore segnala problemi di labilità della struttura e non permette di portare a termine il calcolo. Nelle analisi in frequenza infatti i modi di corpo rigido hanno frequenza 0 Hz: questi modi permettono di identificare facilmente quali sono i componenti non vincolati correttamente. La figura 2 mostra un esempio in cui l’analisi in frequenza permette di determinare la causa di fallimento di un calcolo statico di un serbatoio.
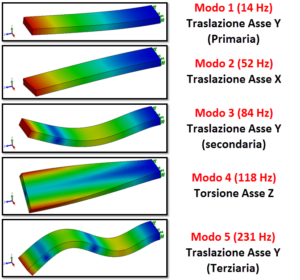
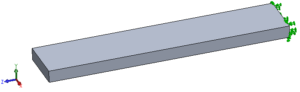
Un’altra applicazione dell’analisi in frequenza è un suo utilizzo per avere delle indicazioni sulla rigidezza della struttura rispetto ai carichi statici e mettere in evidenza quali siano le direzioni in cui è più debole. I modi con frequenze naturali più basse mettono infatti in evidenza le direzioni in cui la struttura offre meno rigidezza. L’esempio di figura 3 (una semplice trave incastrata) chiarisce molto bene questo concetto.
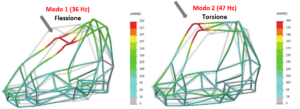
Di conseguenza, l’analisi in frequenza potrebbe essere utilizzata in fase di progetto preliminare (quando non si hanno informazioni molto precise sui carichi e sui vincoli da applicare) per identificare immediatamente le zone più deboli. Nella figura 4 è mostrato un esempio più complesso, ovvero l’analisi applicata ad un telaio di un’auto da corsa. Infine l’analisi in frequenza può essere utilizzata per avere delle indicazioni qualitative sulla risposta della struttura rispetto ai carichi dinamici. Può capitare infatti che modificando una sezione per irrigidire la struttura nei confronti di un carico statico che agisce in una direzione, si abbia come effetto collaterale quello di rendere la struttura più soggetta alle vibrazioni in un’altra direzione a causa dell’aumento della massa (si tenga presente che l’equazione (1) è scritta sia in funzione sia della rigidezza, sia della massa). La figura 5 mostra una chiara dimostrazione di questo effetto sull’esempio della trave incastrata.
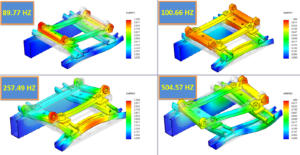Figura 1 – Un motore è montato su una struttura di supporto. La rotazione dell’albero a camme ad una velocità di 2000 giri/min (che corrisponde ad una frequenza di 33,3 Hz) potrebbe provocare delle vibrazioni nella struttura. L’analisi FEM viene svolta su un modello più semplificato in cui vengono omessi i componenti non strutturali e il motore viene trattato come una massa equivalente, concentrata sul baricentro, che scarica sulla struttura delle forze che tengono conto del suo peso e della sua inerzia, e dei momenti dovuti al fatto che la posizione del baricentro del motore non coincide con quella del baricentro della struttura. L’analisi dà come risultato le frequenze proprie e il modo di vibrare (deformata) associata. Le prime due frequenze proprie (89,77 Hz e 100,66 Hz) sono diverse dalla frequenza della forzante (che è 33,3 Hz), ciò indica che la struttura non rischierà di incorrere nel fenomeno della risonanza in cui si verifica una vibrazione incontrollata e sempre più amplificata che potrebbe provocarne il collasso. La prima frequenza propria (89,77 Hz) è compresa nel range da 1 a 3 volte la frequenza del carico (33,3 ÷99,9 Hz): ciò implica che, se si potessero misurare gli spostamenti della struttura durante la vibrazione, questi sarebbero leggermente superiori a quelli che si otterrebbero da un’analisi statica (in cui il software ipotizza la staticità del carico).
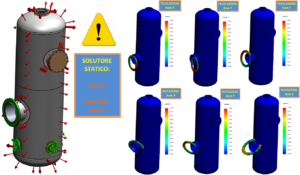Figura 2 – Il calcolo di un’analisi statica su un serbatoio in pressione non va a buon fine perché il solutore segnala un errore di labilità del modello. Si può utilizzare un’analisi in frequenza per determinare la causa della labilità. Nelle analisi in frequenza infatti, i modi propri con frequenza pari a zero corrispondono a modi di corpo libero: le deformate associate a questi modi evidenziano le direzioni in cui si ha labilità del modello. In questo caso il problema è evidentemente una mancanza di connessione tra una flangia ed un tubo perché i primi 6 modi hanno tutti frequenza 0 Hz ed evidenziano i 6 moti rigidi che può compiere la flangia (3 traslazioni e 3 rotazioni).
Figura 3 – L’analisi in frequenza può essere utilizzata per avere indicazioni sulle caratteristiche di rigidezza della struttura e quindi identificare rapidamente quali sono le direzioni in cui la struttura potrebbe deformarsi di più. Effettuando un’analisi delle frequenze proprie su una trave incastrata, la prima frequenza propria (la più bassa – 14 Hz) è associata ad un modo flessionale in direzione verticale (Y), mentre la seconda, decisamente più alta (52 Hz) è associata ad un modo flessionale in direzione orizzontale (X). Ciò concorda pienamente con i risultati che si otterrebbero caricando la trave con una forza statica sulla faccia non vincolata: la struttura, avendo un minor momento di inerzia in direzione Y, tenderebbe a flettere di più se sottoposta ad una forza verticale rispetto ad una forza in direzione orizzontale.
Figura 4 – Analisi di un telaio di un’auto da corsa. I primi due modi di vibrare (il primo flessionale ed il secondo torsionale) evidenziano le zone del telaio che potrebbero risultare più deboli. Questa indicazione porta alla conclusione che sarebbe opportuno porre particolare attenzione nel rinforzare quelle zone per proteggere il pilota in caso di ribaltamento.
Figura 5 – L’analisi in frequenza può essere utilizzata per avere delle indicazioni qualitative sulla risposta della struttura rispetto ai carichi dinamici: si prenda in considerazione la trave incastrata di sezione rettangolare già mostrata in figura 3 e di cui si erano calcolat
e le frequenze proprie. Si supponga di volerla irrigidire per ridurre la flessione in direzione verticale aggiungendo un’ala di altezza 150 mm. Attraverso l’analisi in frequenza sulla nuova geometria si può notare che la frequenza propria del primo modo è aumentata, ad indicare che la struttura si è irrigidita in direzione verticale ma contemporaneamente è diminuita la frequenza propria del secondo modo (flessione in direzione orizzontale). Ciò è dovuto all’incremento della massa della trave, ed indica che, nel caso in cui fosse presente un carico dinamico orizzontale, la trave avrebbe una maggior tendenza a vibrare in quella direzione rispetto alla forma rettangolare.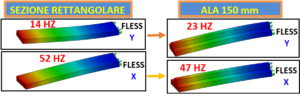
Si supponga di aumentare l’altezza dell’ala progressivamente e si effettuino delle analisi in frequenza per altezze di 230 mm, 300 mm, 380 mm. Si noti che la prima frequenza propria tende sempre più ad aumentare, mentre la seconda tende a diminuire. Quando l’altezza è pari a 380 mm i primi due modi di vibrare si scambiano, ovvero la flessione rispetto a
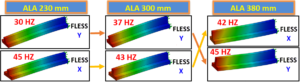ll’asse orizzontale diventa il primo modo di vibrare: ciò indica che la struttura è più rigida rispetto ad un carico statico verticale, ma sarebbe meno “rigida” rispetto ad un carico dinamico orizzontale e tenderebbe a vibrare in quella direzione.
Riquadro 1
